Ламбертовская отражательная способность - Lambertian reflectance

Эта статья нужны дополнительные цитаты для проверка. Пожалуйста помоги улучшить эту статью к добавление цитат в надежные источники. Материал, не полученный от источника, может быть оспорен и удален Найдите источники: «Ламбертовское отражение»  – Новости  · газеты  · книги  · ученый  · JSTOR (Май 2017 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Ламбертовский коэффициент отражения это свойство, определяющее идеальный "матовый" или диффузно отражающий поверхность. Кажущаяся яркость ламбертовской поверхности для наблюдателя одинакова независимо от угла зрения наблюдателя.^[1] С технической точки зрения поверхность яркость является изотропный, а интенсивность света подчиняется Закон косинусов Ламберта. Ламбертовская отражательная способность названа в честь Иоганн Генрих Ламберт, который представил концепцию идеальной диффузии в своей книге 1760 г. Фотометрия.

Примеры

Необработанная древесина демонстрирует примерно ламбертовскую отражательную способность, но древесина покрыта глянцевым слоем полиуретан нет, так как глянцевое покрытие создает зеркальные блики. Свежевыпавший снег и древесный уголь - это приблизительно ламбертовские поверхности с высоким и низким коэффициентом отражения соответственно.^{[нужна цитата ]}. Хотя не все шероховатые поверхности являются ламбертовскими, это часто хорошее приближение и часто используется, когда характеристики поверхности неизвестны.^[2]

Спектралон это материал, который обеспечивает почти идеальную отражательную способность по Ламберту.^[1]

Использование в компьютерной графике

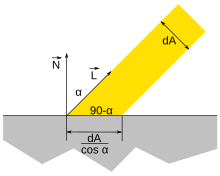
В компьютерная графика, Ламбертовское отражение часто используется как модель для диффузное отражение. Этот метод заставляет все замкнутые полигоны (например, треугольник в 3D-сетке) одинаково отражать свет во всех направлениях при визуализации. Фактически, небольшая плоская область вращалась вокруг своего нормальный вектор не изменит способ отражения света. Тем не менее, эта область изменит способ отражения света, если она будет отклонена от своего исходного вектора нормали, потому что область освещается меньшей частью падающего излучения.^{[3][требуется проверка ]}

Отражение рассчитывается следующим образом: скалярное произведение поверхности нормальный вектор, ${ displaystyle mathbf {N}}$, и нормализованный вектор направления света, ${ displaystyle mathbf {L}}$, указывая с поверхности на источник света. Затем это число умножается на цвет поверхности и силу света, падающего на поверхность:

${ Displaystyle I_ {D} = mathbf {L} cdot mathbf {N} CI_ {L}}$,

куда ${ displaystyle I_ {D}}$ - интенсивность диффузно отраженного света (поверхностная яркость), ${ displaystyle C}$ это цвет и ${ displaystyle I_ {L}}$ это интенсивность падающего света. Потому что

${ Displaystyle mathbf {L} cdot mathbf {N} = | N || L | cos { alpha} = cos { alpha}}$,

куда ${ displaystyle alpha}$ - угол между направлениями двух векторов, интенсивность будет максимальной, если вектор нормали будет указывать в том же направлении, что и вектор света (${ Displaystyle соз {(0)} = 1}$, поверхность будет перпендикулярна направлению света), а наименьшая, если вектор нормали перпендикулярен вектору света (${ Displaystyle соз {( пи / 2)} = 0}$, поверхность проходит параллельно направлению света).

Ламбертовское отражение от полированных поверхностей обычно сопровождается зеркальное отражение (блеск ), где яркость поверхности максимальна, когда наблюдатель находится в направлении идеального отражения (т. е. когда направление отраженного света является отражением направления падающего света на поверхность), и резко падает. Это моделируется в компьютерной графике с различными модели зеркального отражения Такие как Фонг, Кук-Торранс. и Т. Д.^{[нужна цитата ]}

Другие волны

Хотя коэффициент отражения Ламберта обычно относится к отражению света объектом, его можно использовать для обозначения отражения любой волны. Например, в ультразвуковая визуализация говорят, что «грубые» ткани обладают отражательной способностью по Ламберту.^{[нужна цитата ]}

Смотрите также

• Список распространенных алгоритмов затенения
• Гамма-коррекция

Рекомендации