Локальная согласованность - Википедия - Local consistency
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Декабрь 2019 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
В удовлетворение ограничений, местная согласованность условия являются свойствами проблемы удовлетворения ограничений связанный с последовательность подмножеств переменных или ограничений. Их можно использовать для уменьшения пространства поиска и облегчения решения проблемы. Используются различные виды условий локальной согласованности, в том числе: согласованность узлов, согласованность дуги, и согласованность пути.
Каждое условие локальной согласованности может быть усилено преобразованием, которое изменяет проблему без изменения ее решений. Такое преобразование называется распространение ограничений. Распространение ограничений работает за счет сокращения областей переменных, усиления ограничений или создания новых. Это приводит к сокращению пространства поиска, что упрощает решение проблемы с помощью некоторых алгоритмов. Распространение ограничений также может использоваться как средство проверки на неудовлетворенность, неполное в целом, но полное в некоторых частных случаях.
Условия локальной согласованности можно сгруппировать по различным классам. Исходные условия локальной согласованности требуют, чтобы каждое согласованное присвоение можно было последовательно расширить до другой переменной. Направленная согласованность требует, чтобы это условие выполнялось только в том случае, если другая переменная выше, чем те, что указаны в назначении, в соответствии с заданным порядком. Реляционная согласованность включает расширения для более чем одной переменной, но это расширение требуется только для удовлетворения заданного ограничения или набора ограничений.
Предположения
В этой статье проблема удовлетворения ограничений определяется как набор переменных, набор доменов и набор ограничений. Переменные и домены связаны: домен переменной содержит все значения, которые может принимать переменная. Ограничение состоит из последовательности переменных, называемых его областью действия, и набора их оценок, которые являются оценками. удовлетворение ограничение.
Предполагается, что проблемы удовлетворения ограничений, упомянутые в этой статье, имеют особую форму. Проблема в нормализованная форма, соответственно обычная форма, если каждая последовательность переменных является областью действия не более одного ограничения или ровно одного ограничения. Предположение о регулярности сделано только для бинарные ограничения приводит к стандартизированная форма. Эти условия всегда можно обеспечить, объединив все ограничения для последовательности переменных в одну и / или добавив ограничение, которому удовлетворяют все значения последовательности переменных.
На рисунках, использованных в этой статье, отсутствие связи между двумя переменными указывает на то, что между этими двумя переменными не существует ограничений или ограничений, удовлетворяющих всем значениям.[требуется разъяснение ]
Локальная согласованность
Все «стандартные» условия локальной согласованности требуют, чтобы все согласованные частичные оценки могли быть расширены на другую переменную таким образом, чтобы результирующее присвоение было согласованным. Частичная оценка является непротиворечивой, если она удовлетворяет всем ограничениям, область действия которых является подмножеством присвоенных переменных.[требуется разъяснение ]
Согласованность узлов
Согласованность узла требует, чтобы каждое унарное ограничение на переменную удовлетворялось всеми значениями в области определения переменной, и наоборот. Это условие можно тривиально выполнить, уменьшив область определения каждой переменной до значений, которые удовлетворяют всем унарным ограничениям на эту переменную. В результате унарными ограничениями можно пренебречь и считать, что они включены в области.
Например, учитывая переменную с доменом и ограничение , согласованность узлов ограничит домен и тогда ограничение можно было бы отбросить. Этот этап предварительной обработки упрощает последующие этапы.
Стабильность дуги
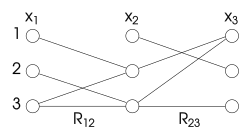
Переменная в задаче удовлетворения ограничений является дуговой согласованной с другой, если каждое из ее допустимых значений согласовано с некоторым допустимым значением второй переменной. Формально переменная согласовано с другой переменной если для каждого значения в области существует ценность в области такой, что удовлетворяет двоичному ограничению между и . Проблема является дуговой согласованной, если каждая переменная согласована по дуге со всеми остальными.
Например, рассмотрим ограничение где переменные находятся в диапазоне от 1 до 3. Поскольку никогда не может быть 3, нет дуги от 3 до значения в так что безопасно удалить. Так же, никогда не может быть 1, поэтому дуги нет, поэтому ее можно удалить.
Согласованность по дуге также может быть определена относительно конкретного двоичного ограничения: двоичное ограничение согласовано с дугой, если каждое значение одной переменной имеет значение второй переменной, так что они удовлетворяют ограничению. Это определение согласованности дуги аналогично приведенному выше, но дается для конкретного ограничения. Это различие особенно актуально для ненормализованных задач, где в приведенном выше определении учитываются все ограничения между двумя переменными, а в этом - только конкретная.
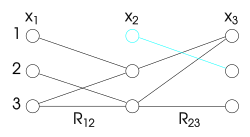
Если переменная не согласуется с другой, это можно сделать так, удалив некоторые значения из ее домена. Это форма распространения ограничений, которая обеспечивает согласованность дуги: она удаляет из области определения переменной каждое значение, которое не соответствует значению другой переменной. Это преобразование поддерживает решения проблемы, так как удаленные значения в любом случае не являются решением.
Распространение ограничений может сделать всю дугу задачи согласованной, повторив это удаление для всех пар переменных. В этом процессе может потребоваться рассмотреть данную пару переменных более одного раза. Действительно, удаление значений из области определения переменной может привести к тому, что другие переменные больше не будут согласованы с ней. Например, если соответствует ли дуга но алгоритм уменьшает область , дуговая согласованность с больше не действует и требует повторного принуждения.
Упрощенный алгоритм будет циклически перебирать пары переменных, обеспечивая согласованность по дуге, повторяя цикл до тех пор, пока в течение всего цикла не изменится ни одна область. В Алгоритм AC-3 улучшается по сравнению с этим алгоритмом, игнорируя ограничения, которые не были изменены с момента последнего анализа. В частности, он работает с набором ограничений, который изначально содержит их все; на каждом шаге он устанавливает ограничение и обеспечивает согласованность дуги; если эта операция могла привести к нарушению согласованности дуги по другому ограничению, она помещает его обратно в набор ограничений для анализа. Таким образом, как только для ограничения применяется согласованность по дуге, это ограничение не учитывается снова, если не изменен домен одной из его переменных.
Согласованность пути
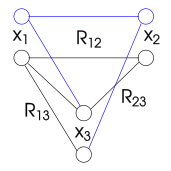
Согласованность пути - это свойство, подобное согласованности дуги, но учитывает пары переменных, а не только одну. Пара переменных согласована по пути с третьей переменной, если каждую согласованную оценку пары можно распространить на другую переменную таким образом, что все двоичный ограничения выполнены. Формально, и путь согласуется с если для каждой пары значений который удовлетворяет двоичному ограничению между и , существует значение в области такой, что и удовлетворить ограничение между и и между и , соответственно.
Форма распространения ограничения, обеспечивающая согласованность пути, работает путем удаления из ограничения некоторого удовлетворительного назначения. Действительно, согласованность пути может быть обеспечена путем удаления из двоичного ограничения всех оценок, которые не могут быть распространены на другую переменную. Что касается согласованности дуги, при этом удалении, возможно, придется учитывать двоичное ограничение более одного раза. Что касается согласованности дуги, результирующая проблема имеет те же решения, что и исходная, поскольку удаленные значения не являются решением.
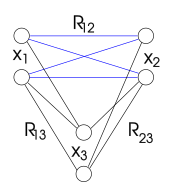
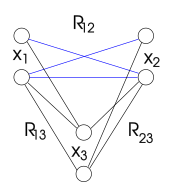
Форма распространения ограничений, обеспечивающая согласованность пути, может ввести новые ограничения. Когда две переменные не связаны двоичным ограничением, они фактически связаны ограничением, допускающим любую пару значений. Однако некоторая пара значений может быть удалена при распространении ограничения. Результирующее ограничение больше не удовлетворяется всеми парами значений. Следовательно, это больше не виртуальное, тривиальное ограничение.
Название «согласованность путей» происходит от исходного определения, в котором использовалась пара переменных и путь между ними, а не пара и единственная переменная. Хотя эти два определения различны для одной пары переменных, они эквивалентны в отношении всей проблемы.
Обобщения
Согласованность дуги и пути можно обобщить на небинарные ограничения, используя кортежи переменных вместо одной или пары. Кортеж переменные -соответствует другой переменной, если каждая последовательная оценка переменные могут быть расширены значением другой переменной при сохранении согласованности. Это определение очевидным образом распространяется на все проблемы. Сильный -согласованность -системность для всех .
Частный случай 2-непротиворечивости совпадает с дуговой непротиворечивостью (в этой статье все задачи считаются узловыми). С другой стороны, 3-согласованность совпадает с согласованностью пути только в том случае, если все ограничения являются двоичными, потому что согласованность пути не включает тройных ограничений, в то время как согласованность 3-х делает.
Другой способ обобщения согласованности дуги - гипер-дуговая согласованность или же обобщенная согласованность дуги, который требует расширяемости одной переменной для удовлетворения ограничения. А именно, переменная является гипер-дугой, согласованной с ограничением, если каждое значение переменной может быть расширено до других переменных ограничения таким образом, чтобы ограничение удовлетворялось.
Последовательность и выполнимость
Распространение ограничений (обеспечение локальной согласованности) может привести к пустому домену или неудовлетворительный ограничение. В этом случае у проблемы нет решения. Обратное неверно в общем случае: несогласованный экземпляр может быть согласованным по дуге или по пути, не имея при этом пустой области или невыполнимых ограничений.
Действительно, локальная согласованность относится только к согласованности групп переменных. Например, согласованность дуги гарантирует, что каждая последовательная оценка переменной может быть последовательно расширена до другой переменной. Однако, когда одно значение переменной расширяется до двух других переменных, нет гарантии, что эти два значения согласуются друг с другом. Например, может соответствовать и с , но эти две оценки могут не соответствовать друг другу.
Однако в некоторых случаях для доказательства выполнимости можно использовать распространение ограничений. Набор двоичных ограничений, согласованный по дуге и не имеющий пустой области, может быть несовместимым, только если сеть ограничений содержит циклы. В самом деле, если ограничения являются двоичными и образуют ациклический граф, значения всегда можно распространять по ограничениям: для каждого значения переменной все переменные в ограничении с ним имеют значение, удовлетворяющее этому ограничению. В результате решение может быть найдено путем итеративного выбора неназначенной переменной и рекурсивного распространения через ограничения. Этот алгоритм никогда не пытается присвоить значение уже назначенной переменной, поскольку это подразумевает наличие циклов в сети ограничений.
Аналогичное условие выполняется для согласованности путей. Ниже перечислены частные случаи, в которых выполнимость может быть установлена путем обеспечения согласованности дуги и согласованности путей.
- обеспечение согласованности дуги устанавливает выполнимость задач, состоящих из двоичных ограничений без циклы (а дерево бинарных ограничений);
- обеспечение согласованности путей устанавливает выполнимость бинарных ограничений (возможно, с циклами) с бинарными доменами;
- обеспечение сильного последовательность устанавливает выполнимость проблем, содержащих переменные.
Особые случаи
Некоторые определения или результаты об относительной непротиворечивости применимы только в особых случаях.
Когда домены состоят из целые числа, связность может быть определена. Эта форма согласованности основана на согласованности крайних значений областей, то есть минимальных и максимальных значений, которые может принимать переменная.
Когда ограничения алгебраический или же Булево, согласованность дуги эквивалентна добавлению нового ограничения или синтаксическому изменению старого, и это может быть сделано путем составления соответствующих ограничений.
Специализированные ограничения
Обычно используются некоторые виды ограничений. Например, часто используется ограничение, что некоторые переменные все разные. Существуют эффективные специализированные алгоритмы для обеспечения согласованности дуги при таких ограничениях.
Ограничение, заставляющее ряд переменных отличаться, обычно записывается или же все разные ([X1, ..., Xn]). Это ограничение эквивалентно неравенству всех пар различных переменных, то есть для каждого . Когда домен переменной сокращается до единственного значения, это значение может быть удалено из всех других доменов путем распространения ограничения при обеспечении согласованности дуги. Использование специального ограничения позволяет использовать свойства, которые не выполняются для отдельных двоичных файлов. неравенство.
Первое свойство состоит в том, что общее количество элементов в доменах всех переменных должно быть не меньше количества переменных. Точнее, после обеспечения согласованности дуги количество неназначенных переменных не должно превышать количество значений в объединении их доменов. В противном случае ограничение не может быть выполнено. Это условие легко проверить на ограничении в все разные формы, но не соответствует дуге непротиворечивости сети неравенств. Второе свойство сингла все разные ограничение состоит в том, что согласованность гипердуги можно эффективно проверить с помощью двудольное соответствие алгоритм. В частности, граф строится с переменными и значениями как двумя наборами узлов, и на нем запускается специализированный алгоритм сопоставления двудольных графов, чтобы проверить наличие такого сопоставления.
Другой тип ограничения, который обычно используется, - это совокупный один. Он был введен для задач планирования и размещения. В качестве примера, кумулятивная ([S1, ..., Sm], [D1, ..., Dm], [R1, ..., Rm], L) можно использовать для формализации состояния, в котором находятся м мероприятия, каждое со временем начала си, продолжительность ди и используя сумму ри ресурса. В ограничении указано, что общий доступный объем ресурсов равен L. Существуют специализированные методы распространения ограничений для кумулятивных ограничений; используются разные методы в зависимости от того, какие вариабельные домены уже сокращены до одного значения.
Третье специализированное ограничение, которое используется в программирование логики ограничений это элемент один. В программировании логики ограничений списки разрешены как значения переменных. Ограничение элемент (I, L, X) удовлетворен, если L это список и Икс это я-й элемент этого списка. Для этих ограничений существуют специальные правила распространения ограничений. Например, если L и я сводятся к однозначной области, уникальному значению для Икс можно определить. В более общем смысле, невозможные значения Икс можно вывести из области наоборот.
Направленная согласованность
Направленная согласованность - это вариант дуги, пути и -согласованность, адаптированная для использования алгоритмом, который присваивает значения переменным в соответствии с заданным порядком переменных. Они похожи на их ненаправленные аналоги, но требуют только, чтобы согласованное присвоение некоторым переменным могло быть последовательно расширено на другую переменную, которая больше их в соответствии с порядком.
Направленная дуга и согласованность пути
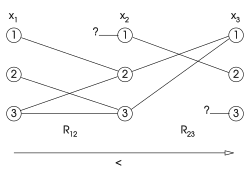
Если алгоритм оценивает переменные в порядке , согласованность полезна только тогда, когда она гарантирует, что все значения переменных с более низким индексом согласуются со значениями переменных с более высоким индексом.
При выборе значения для переменной значениями, несовместимыми со всеми значениями неназначенной переменной, можно пренебречь. Действительно, даже если все эти значения согласуются с текущей частичной оценкой, алгоритм позже не сможет найти согласованное значение для неназначенной переменной. С другой стороны, обеспечение согласованности с переменными, которые уже оцениваются, необязательно: если алгоритм выбирает значение, несовместимое с текущей частичной оценкой, несогласованность обнаруживается в любом случае.
Предполагая, что порядок оценки переменных равен , проблема удовлетворения ограничений является направленно-дуговой согласованной, если каждая переменная согласуется ли дуга с любой другой переменной такой, что . Согласованность направленного пути аналогична, но две переменные должен соответствовать пути только если . Сильная согласованность направленного пути означает согласованность как направленного пути, так и согласованности направленной дуги. Аналогичные определения могут быть даны для других форм согласованности.
Распространение ограничений для согласованности дуги и пути
Распространение ограничений, обеспечивающее согласованность направленной дуги, выполняет итерацию по переменным от последней к первой, обеспечивая на каждом шаге согласованность с ней каждой переменной с более низким индексом. Если порядок переменных , этот алгоритм перебирает переменные из к ; для переменной , он обеспечивает согласованность по дуге каждой переменной с индексом ниже, чем с .
 | 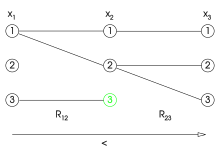 |  |
| Экземпляр, который не соответствует направленной дуге: не соответствует никакому значению и не соответствует никакому значению . Нет ограничений между и (соответствующие ребра опущены). | Обеспечение согласованности направленной дуги начинается с , и делает дуга согласуется с ним, удаляя значение . | Обеспечение согласованности направленной дуги выполняется с помощью . С уже удалено, оба и удалены. |
Согласованность направленного пути и строгая согласованность направленного пути может быть обеспечена с помощью алгоритмов, аналогичных алгоритму согласованности дуги. Они обрабатывают переменные из к ; для каждой переменной две переменные с рассматриваются, и согласованность пути их с принудительно. Никаких операций не требуется, если проблема не содержит ограничения на и или нет ограничений между и . Однако, даже если между и , предполагается тривиальный. Если распространение ограничения сокращает свой набор удовлетворяющих назначений, оно эффективно создает новое нетривиальное ограничение. Распространение ограничений, обеспечивающее строгую согласованность направленного пути, аналогично, но также обеспечивает согласованность дуги.
Направленная последовательность и выполнимость
Направленная согласованность гарантирует, что частичные решения, удовлетворяющие ограничению, могут быть последовательно расширены до другой переменной с более высоким индексом. Однако это не гарантирует, что расширения различных переменных совместимы друг с другом. Например, частичное решение может быть последовательно расширено до переменной или изменить , но все же эти два расширения не согласуются друг с другом.
Есть два случая, когда этого не происходит, и согласованность по направлениям гарантирует выполнимость, если ни один домен не является пустым и никакое ограничение не является невыполнимым.
Первый случай - это проблема двоичных ограничений с упорядочением переменных, которое делает упорядоченный граф ограничения, имеющие ширина 1. Такой порядок существует тогда и только тогда, когда граф ограничений является деревом. Если это так, ширина графа ограничивает максимальное количество нижних (в соответствии с порядком) узлов, к которым присоединяется узел. Согласованность направленной дуги гарантирует, что каждое согласованное присвоение переменной может быть расширено на более высокие узлы, а ширина 1 гарантирует, что узел не присоединен более чем к одному нижнему узлу. В результате, как только нижняя переменная назначена, ее значение может быть последовательно расширено до каждой более высокой переменной, с которой она связана. Это расширение не может впоследствии привести к несогласованности. Действительно, никакая другая более низкая переменная не присоединяется к этой более высокой переменной, поскольку ширина графика равна 1.
В результате, если проблема ограничения имеет ширину 1 относительно упорядочения ее переменных (что подразумевает, что соответствующий ей граф является деревом) и проблема является направленно-дуговой согласованной относительно того же порядка, решение (если есть) можно найти путем итеративного присвоения переменных в соответствии с порядком.
Второй случай, в котором направленная согласованность гарантирует выполнимость, если ни одна область не пуста, и никакое ограничение не является неудовлетворенным, - это проблема двоичных проблем с ограничениями, граф которых имеет наведенная ширина 2, используя сильную согласованность направленного пути. Действительно, эта форма согласованности гарантирует, что каждое присвоение переменной или паре переменных может быть расширено до более высокой переменной, а ширина 2 гарантирует, что эта переменная не будет присоединена к другой паре более низких переменных.
Причина, по которой наведенная ширина рассматривается вместо ширины, заключается в том, что обеспечение согласованности направленного пути может добавить ограничения. Действительно, если две переменные не находятся в одном ограничении, но находятся в ограничении с более высокой переменной, некоторые пары их значений могут нарушить согласованность пути.Удаление таких пар создает новое ограничение. В результате распространение ограничений может привести к проблеме, граф которой имеет больше ребер, чем исходный. Однако все эти ребра обязательно находятся в индуцированном графе, поскольку все они находятся между двумя родителями одного и того же узла. Ширина 2 гарантирует, что каждая согласованная частичная оценка может быть расширена до решения, но эта ширина зависит от созданного графика. В результате, наведенная ширина, равная 2, требуется для сильной согласованности направленности траектории, чтобы гарантировать существование решений.
Направленная i-согласованность

Направленный -согласованность - это гарантия того, что каждое последовательное присвоение переменные могут быть последовательно расширены до другой переменной, которая находится выше по порядку. Сильное направленное -согласованность определяется аналогично, но все группы в большинстве рассматриваются переменные. Если проблема строго направлена -согласованный и имеет ширину менее и не имеет пустого домена или невыполнимых ограничений, у него есть решения.
Каждую проблему можно решить строго направленно -согласованный, но эта операция может увеличить ширину соответствующих ей графиков. Процедура распространения ограничений, обеспечивающая согласованность по направлениям, аналогична процедуре, используемой для согласованности по дуге и согласованности по пути. Переменные рассматриваются по очереди, от последней к первой в соответствии с порядком. Для переменной , алгоритм рассматривает каждую группу переменные с индексом ниже и находятся в затруднительном положении с . Согласованность этих переменных с проверяется и, возможно, выполняется путем удаления удовлетворяющих назначений из ограничения среди всех этих переменные (если есть, или создание новых в противном случае).

Эта процедура генерирует строго направленный -согласованный экземпляр. Однако он также может добавить к экземпляру новые ограничения. В результате, даже если ширина исходной задачи равна , ширина полученного экземпляра может быть больше. Если это так, направленная строгая согласованность не подразумевает выполнимости, даже если ни один домен не является пустым и никакое ограничение не является невыполнимым.
Однако распространение ограничений добавляет ограничения только к переменным, которые ниже, чем та, которую он в настоящее время рассматривает. В результате никакие ограничения на переменную не изменяются и не добавляются после того, как алгоритм обработал эту переменную. Вместо того, чтобы рассматривать фиксированный , можно изменить его на количество родителей каждой рассматриваемой переменной (родители переменной - это переменные с индексом ниже, чем переменная, и которые находятся в ограничении с переменной). Это соответствует рассмотрению всех родителей данной переменной на каждом шаге. Другими словами, для каждой переменной от последнего до первого, все его родители включаются в новое ограничение, которое ограничивает их значения теми, которые согласуются с . Поскольку этот алгоритм можно рассматривать как модификацию предыдущего со значением который изменяется на количество родителей каждого узла, он называется адаптивная согласованность.
Этот алгоритм обеспечивает строго направленное -соответствие равной наведенной ширине задачи. Результирующий экземпляр является выполнимым тогда и только тогда, когда ни один домен или ограничение не становятся пустыми. В этом случае решение можно легко найти, итеративно устанавливая неназначенной переменной произвольное значение и распространяя эту частичную оценку на другие переменные. Этот алгоритм не всегда является полиномиальным, поскольку количество ограничений, вводимых путем обеспечения строгой согласованности по направлениям, может привести к экспоненциальному увеличению размера. Однако проблема решается в полиномиальное время если принудительная строгая согласованность направлений не суперполиномиально увеличить экземпляр. В результате, если у экземпляра индуцированная ширина ограничена константой, его можно решить за полиномиальное время.
Устранение ведра
Исключение ведра - это алгоритм выполнимости. Его можно определить как переформулировку адаптивной согласованности. В его определениях используются корзины, которые являются контейнерами для ограничения, каждая переменная имеет связанную корзину. Ограничение всегда принадлежит сегменту самой высокой переменной.
Алгоритм исключения корзины поочередно переходит от самой высокой переменной к самой низкой. На каждом шаге ограничения в сегментах этой переменной считаются. По определению, эти ограничения включают только переменные ниже, чем . Алгоритм изменяет ограничение между этими более низкими переменными (если они есть, в противном случае он создает новую). В частности, это требует, чтобы их значения могли быть расширены до в соответствии с ограничениями в ведре . Это новое ограничение, если оно есть, затем помещается в соответствующую корзину. Поскольку это ограничение включает только переменные ниже, чем , он добавляется в корзину переменной, которая ниже, чем .
Этот алгоритм эквивалентен обеспечению адаптивной согласованности. Поскольку оба они обеспечивают согласованность переменной со всеми ее родителями, и поскольку новое ограничение не добавляется после того, как переменная рассматривается, в результате получается экземпляр, который можно решить без возврат.
Поскольку граф создаваемого ими экземпляра является подграфом индуцированного графа, если индуцированная ширина ограничена константой, сгенерированный экземпляр имеет размер, полиномиальный размеру исходного экземпляра. В результате, если индуцированная ширина экземпляра ограничена константой, решение может быть выполнено за полиномиальное время двумя алгоритмами.
Реляционная согласованность
В то время как предыдущие определения согласованности все касались согласованности назначений, реляционная согласованность включает только выполнение данного ограничения или набора ограничений. Точнее, реляционная непротиворечивость подразумевает, что каждое непротиворечивое частичное присваивание может быть расширено таким образом, чтобы удовлетворялось данное ограничение или набор ограничений. Формально ограничение по переменным реляционно согласованно с одной из своих переменных если каждое последовательное задание может быть расширен до в таком случае доволен. Разница между "обычным" Непротиворечивость и непротиворечивость реляционной дуги заключается в том, что последняя требует только расширенного присваивания для удовлетворения заданного ограничения, в то время как первая требует, чтобы оно удовлетворяло всем соответствующим ограничениям.
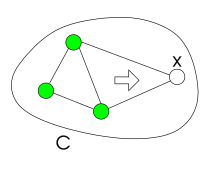

Это определение может быть расширено до более чем одного ограничения и более чем одной переменной. В частности, реляционная согласованность путей аналогична реляционной дуговой согласованности, но вместо одного используются два ограничения. Два ограничения являются реляционными путями, согласованными с переменной, если каждое согласованное присвоение всем их переменным, кроме рассматриваемого, может быть расширено таким образом, чтобы эти два ограничения были удовлетворены.
Для более чем двух ограничений реляционные -согласованность определяется. Реляционный -согласованность предполагает набор ограничения и переменная, которая находится в области действия всех этих ограничений. В частности, эти ограничения реляционные -согласованно с переменной, если каждое согласованное присвоение всем другим переменным, находящимся в их области действия, может быть расширено до переменной таким образом, чтобы эти ограничения были удовлетворены. Проблема в том -отношения согласованы, если каждый набор ограничения реляционные -соответствует каждой переменной, которая присутствует во всех областях. Сильные отношения согласованность определяется, как указано выше: это свойство быть реляционным -соответствует каждому .
Реляционная согласованность также может быть определена для большего количества переменных вместо одной. Набор ограничения реляционные -согласованным, если каждое последовательное присвоение подмножеству их переменных можно расширить до оценки всех переменных, удовлетворяющих всем ограничениям. Это определение не является точным расширением вышеизложенного, поскольку переменные, на которые предполагается распространить оценки, не обязательно входят во все области задействованных ограничений.
Если указан порядок переменных, реляционная согласованность может быть ограничена случаями, когда переменные (ы) оценки должны быть расширяемыми, чтобы следовать за другими переменными в порядке. Это измененное условие называется направленной реляционной согласованностью.
Относительная согласованность и выполнимость
Проблема удовлетворения ограничений может быть реляционно непротиворечивой, не иметь пустой области или невыполнимых ограничений, но при этом быть неудовлетворительной. Однако в некоторых случаях это невозможно.
Первый случай - это сильно реляционный -согласованная проблема, когда домены содержат не более элементы. В этом случае последовательная оценка переменные всегда можно расширить до одной другой переменной. Если такая оценка и это переменная, есть только возможные значения, которые может принимать переменная. Если все такие значения несовместимы с оценкой, есть (не обязательно уникальные) ограничения, которые нарушаются оценкой и одним из ее возможных значений. В результате оценка не может быть расширена для удовлетворения всех этих требований. -или менее ограничений, нарушающих условие сильной реляционной -последовательность.
Второй случай связан с мерой ограничений, а не с областями. Ограничение -tight, если каждое вычисление ко всем его переменным, кроме одной, может быть расширено для удовлетворения ограничения либо всеми возможными значениями другой переменной, либо не более чем его ценностей. Проблема с -жатые ограничения выполнимы тогда и только тогда, когда они строго реляционно -последовательный.

Третий случай - это бинарные ограничения, которые могут быть представлены выпуклыми по строкам матрицами. Бинарное ограничение может быть представлено двумерной матрицей , куда равно 0 или 1 в зависимости от того, -ое значение домена и -ое значение домена удовлетворить ограничение. Строка этой матрицы является выпуклой, если содержащиеся в ней единицы являются последовательными (формально, если два элемента равны 1, все элементы между ними также равны 1). Матрица называется выпуклой по строке, если все ее строки выпуклы.

Условие, которое делает сильную реляционную согласованность путей эквивалентной выполнимости, - это условие выполнения задач удовлетворения ограничений, для которых существует такой порядок переменных, при котором все ограничения должны быть представлены выпуклыми матрицами по строкам. Этот результат основан на том факте, что набор выпуклых строк, имеющих попарно общий элемент, также имеет глобально общий элемент. Учитывая, что оценка закончилась переменных, допустимые значения для -е задаются путем выбора нескольких строк из некоторых ограничений. В частности, для каждой переменной среди единица, строка относительно его значения в матрице, представляющая ограничение, связывающее ее с один представляет допустимые значения последнего. Поскольку эти строки являются выпуклыми и имеют общий элемент попарно из-за согласованности путей, они также имеют общий общий элемент, который представляет значение последней переменной, согласованное с другими.
Использование локальной последовательности
Все формы локальной согласованности могут быть усилены распространением ограничений, которое может уменьшить области переменных и наборы назначений, удовлетворяющих ограничению, и может ввести новые ограничения. Всякий раз, когда распространение ограничений создает пустую область или невыполнимое ограничение, исходная проблема становится неудовлетворительной. Следовательно, все формы локальной согласованности могут использоваться как приближения выполнимости. Точнее, их можно использовать в качестве алгоритмов неполной невыполнимости, поскольку они могут доказать, что проблема невыполнима, но в целом не могут доказать, что проблема выполнима. Такие приближенные алгоритмы могут использоваться алгоритмами поиска (возврат, обратный прыжок, местный поиск и т. д.) в качестве эвристики для определения возможности расширения частичного решения для удовлетворения всех ограничений без дальнейшего его анализа.
Даже если распространение ограничений не приводит к пустой области или неудовлетворительному ограничению, тем не менее, оно может уменьшить области или усилить ограничения. Если это так, пространство поиска проблемы уменьшается, тем самым уменьшая объем поиска, необходимый для решения проблемы.
Локальная согласованность доказывает выполнимость в некоторых ограниченных случаях (см. Сложность удовлетворения ограничений # Ограничения ). Это имеет место для каких-то особых проблем и / или некоторых видов локальной согласованности. Например, обеспечение согласованности дуги для двоичных ациклических задач позволяет определить, является ли проблема выполнимой. Обеспечение сильной направленности -согласованность позволяет сказать выполнимость задач, которые имеют наведенную ширину в том же порядке. Адаптивная направленная согласованность позволяет говорить о выполнимости произвольной задачи.
Смотрите также
- Распространение единицы
- Ограниченное программирование
- Программирование логики ограничений
- Прогнозирование (возврат)
внешняя ссылка
- Ограничение распространения - Диссертация Гвидо Такка, дающая хороший обзор теории и вопросов реализации.
Рекомендации
- Лекутр, Кристоф (2009). Сети ограничений: методы и алгоритмы. ISTE / Wiley. ISBN 978-1-84821-106-3
- Дехтер, Рина (2003). Обработка ограничений. Морган Кауфманн. ISBN 1-55860-890-7
- Апт, Кшиштоф (2003). Принципы программирования ограничений. Издательство Кембриджского университета. ISBN 0-521-82583-0
- Marriott, Ким; Питер Дж. Стаки (1998). Программирование с ограничениями: введение. MIT Press. ISBN 0-262-13341-5





















































