MLAB - Википедия - MLAB
Эта статья нужны дополнительные цитаты для проверка. (Август 2015 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
 | |
| Разработчики) | Civilized Software Inc. |
|---|---|
| изначальный выпуск | 1985 |
| Написано в | C, Ассемблер, MLAB [1] |
| Операционная система | Кроссплатформенность: Майкрософт Виндоус, Linux, и Mac OS X |
| Платформа | IA-32, x86-64 |
| Тип | Численные вычисления |
| Лицензия | Проприетарный коммерческое программное обеспечение |
| Интернет сайт | www |
| Парадигма | мультипарадигма: функциональный, императив, процедурный, множество |
|---|---|
| Разработано | Гэри Д. Нотт, Дэниел Р. Кернер и Барри Буноу |
| Разработчик | Цивилизованное программное обеспечение |
| Впервые появился | конец 1970-х |
| Печатная дисциплина | динамичный, слабый |
| Операционные системы | Кроссплатформенность |
| Интернет сайт | www |
| |
MLAB (Mодевание LABораторское искусство) является мультипарадигма числовые вычисления окружающая среда и язык программирования четвертого поколения.
А собственный язык программирования Разработанный Civilized Software, Inc., MLAB позволяет матрица манипуляции, построение функции и данные, и реализация алгоритмы, и обеспечивает поддержку аппроксимации кривой, дифференциальных уравнений, статистики и графики.
MLAB предназначен для численных вычислений, со специальными средствами для обыкновенное дифференциальное уравнение -решение (ODE-решение) и подгонка кривой (нелинейная регрессия.) Он предоставляет более тридцати типов команд и более 450 встроенных функций из областей элементарной математики, трансцендентных функций, вероятностей и статистики, линейной алгебры, оптимизации, кластерного анализа, комбинаторики, числового ввода / вывода. , и графика.
Обычные низкоуровневые функции, например синус, косинус, логарифм и т. д., а также функции, выполняющие более сложный анализ, такие как разложение по сингулярным числам, дискретные преобразования Фурье, решение систем дифференциальных уравнений, непараметрическое моделирование и нелинейная оптимизация с ограничениями, среди многих другие. Включен значительный набор статистически ориентированных функций, таких как наиболее распространенные функции распределения и их обратные, а также надежные функции создания графиков, поддерживающие построение графиков исключительно сложных функций.
Многие программные пакеты могут интегрировать обыкновенные дифференциальные уравнения численно, но MLAB - один из немногих, который также может регулировать параметры и начальные условия. MLAB одинаково легко справляется с подгонкой кривой, когда корректировки являются линейными или, как в случае с большинством моделей дифференциальных уравнений, нелинейными.
MLAB широко используется в академических и исследовательских учреждениях, а также на промышленных предприятиях.
История
MLAB был первоначально разработан в Национальный институт здоровья в конце 1970-х с использованием Стэнфорд с ПЛЫТЬ работает на Корпорация цифрового оборудования (DEC) PDP-10 компьютеры. Создатели MLAB основали Civilized Software, Inc. в 1985 году и расширили MLAB в конце 1980-х - начале 1990-х годов за счет применения Исследование инноваций малого бизнеса гранты.
MLAB впервые был принят исследователями и практиками в области биохимии, но быстро распространился на многие другие области. Сейчас он также используется в образовании, в частности, при обучении линейная алгебра, числовой анализ, и популярен среди ученых, занимающихся химическая кинетика анализ и моделирование[2] и компартментальное моделирование в фармакологии (включая фармакокинетика ) и физиологические исследования.
Синтаксис
Приложение MLAB построено на языке сценариев MLAB. Обычно приложение MLAB используется в командном окне в качестве интерактивного математического или исполняемого текстового файла (скрипта), содержащего код MLAB.
Существуют десятки команд MLAB и сотни функций MLAB. По сути, MLAB - это интерпретатор математического языка высокого уровня с возможностью обработки повторно запускаемых файлов сценариев, называемых do-файлами.
Пример
В MLAB можно определить функцию и построить график ее следующим образом.
функция f (x) = a * cos (b * x) * exp (-k * x) a = 1; b = 4; k = 0,5 v = 1:10! 100 m = точки (f, v) нарисовать m вид
В результате получился простой сюжет:
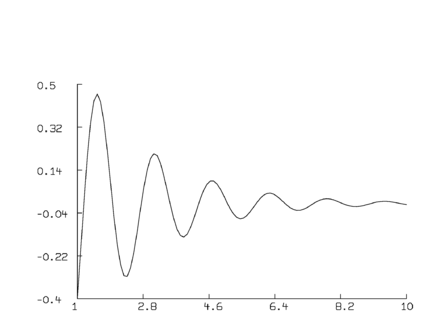
Обратите внимание, что 1:10!100 = 1: 10: 0,0909090909, что означает, что мы имеем дело с вектором-столбцом со значениями от 1 до 10 с шагом 0,0909090909.
Также обратите внимание, что точки (f, v) = v & '(f на v), и это v $ '(f на v) означает конкатенацию матрицы по столбцам v вектор-столбец того же размера, состоящий из значений ж вычисляется на значениях в v.
Можно считывать 110 значений данных из файла в матрицу с двумя столбцами следующим образом (в результате получается матрица размером 55 строк на 2 столбца).
d = читать ("имя файла"; 55,2)Взяв строки матрицы d как (x, y) точки данных - с ошибкой в значениях y - где эти точки данных "моделируются" функцией ж, определенных выше, можно оценить неизвестные параметры а,б,k следующее.
подходят (a, b, k), от f до d
Можно использовать оценочные веса для различных точек данных в d на основе функции оценки скользящей дисперсии ewt следующее.
fit (a, b, k), от f до d с wt ewt (d)
Можно изобразить данные и "соответствие" следующим образом.
удалить w / *, чтобы удалить любое предыдущее изображение * / рисовать d тип линии нет, точки рисования точечного круга (f, d col 1) цвет зеленый вид
Можно посмотреть на символическую производную от ж и изобразите его следующим образом.
введите f'x точки рисования (f'x, d col 1) цвет красный вид
Обратите внимание, что MLAB может использовать символические производные, когда производные значения необходимы во время аппроксимации кривой или решения ODE. Также обратите внимание, что можно подогнать (или просто решить) модели, определенные дифференциальным уравнением, в MLAB, чтобы можно было обрабатывать химическую кинетику, физиологические и компартментные модели.
Смотрите также
Рекомендации
- ^ «MLAB: продвинутая система математического и статистического моделирования». Civilized Software, Inc. Получено 2015-08-27.
- ^ >«Химическая кинетика: простое связывание: F + G B» (PDF). Civilized Software, Inc. Получено 2015-09-01.
