Управляемость сети - Network controllability

Управление простой сетью.

Управляемость сети озабочен структурным управляемость из сеть. Управляемость описывает нашу способность направлять динамическая система из любого начального состояния в любое желаемое конечное состояние за конечное время с подходящим выбором входов. Это определение хорошо согласуется с нашим интуитивным представлением о контроле. Управляемость общих направленных и взвешенных сложных сетей в последнее время стала предметом интенсивных исследований ряда групп в самых разных сетях по всему миру. Недавние исследования Sharma et al.^[1] в разнотипных биологических сетях (ген-ген, miRNA-ген, сети белок-белкового взаимодействия) идентифицировали контрольные мишени в фенотипически охарактеризованной остеосаркоме, демонстрируя важную роль генов и белков, ответственных за поддержание микросреды опухоли.

Фон

Рассмотрим каноническую линейную инвариантную во времени динамику на сложной сети${ Displaystyle { точка { mathbf {X}}} (t) = mathbf {A} cdot mathbf {X} (t) + mathbf {B} cdot mathbf {u} (t)}$где вектор ${ Displaystyle mathbf {X} (t) = (x_ {1} (t), cdots, x_ {N} (t)) ^ { mathrm {T}}}$ фиксирует состояние системы ${ displaystyle N}$ узлы во время ${ displaystyle t}$. В ${ Displaystyle N раз N}$матрица ${ displaystyle mathbf {A}}$ описывает электрическую схему системы и силу взаимодействия между компонентами. В ${ Displaystyle N раз M}$ матрица ${ displaystyle mathbf {B}}$ идентифицирует узлы, контролируемые внешним контроллером. Система управляется через зависящий от времени вектор ввода ${ displaystyle mathbf {u} (t) = (u_ {1} (t), cdots, u_ {M} (t)) ^ { mathrm {T}}}$ что контроллер накладывает на систему. Чтобы определить минимум количество узлов драйвера, обозначенное ${ Displaystyle N _ { mathrm {D}}}$, чей контроль достаточен для полного управления динамикой системы, Liu et al.^[2] попытался объединить инструменты из теории структурного управления, теории графов и статистической физики. Они показали^[2] что минимальное количество входов или узлов драйверов, необходимых для поддержания полного контроля над сетью, определяется «максимальным соответствием» в сети, то есть максимальным набором ссылок, которые не имеют общих начальных или конечных узлов. На основе этого результата была разработана аналитическая основа, основанная на распределении степени «вход-выход» для прогнозирования ${ Displaystyle п _ { mathrm {D}} = N _ { mathrm {D}} / N}$ для безмасштабных графов и графов Эрдеша – Реньи.^[2] Однако недавно было продемонстрировано, что управляемость сети (и другие структурные методы, которые используют исключительно связность графа, ${ displaystyle mathbf {A}}$, чтобы упростить лежащую в основе динамику), как недооценивать, так и превышать количество и какие наборы узлов драйверов лучше всего управляют динамикой сети, подчеркивая важность избыточности (например, канализации) и нелинейной динамики в определении контроля.^[3]

Также следует отметить, что Liu's et al. формулировка^[2] предсказал бы те же значения ${ Displaystyle {п _ { mathrm {D}}}}$ для цепного графа и для слабо плотносвязного графа. Очевидно, что оба этих графика имеют очень разные внутренние и внешние распределения степеней. Недавняя неопубликованная работа,^[4] вопросы, есть ли степень, который является чисто локальной мерой в сетях, полностью описал бы управляемость и вопрос о том, не будут ли даже немного удаленные узлы играть роль в принятии решения об управляемости сети. Действительно, для многих сетей реального слова, а именно пищевых сетей, нейронных и метаболических сетей, несоответствие значений ${ Displaystyle {п _ { mathrm {D}}} ^ {настоящий}}$ и ${ Displaystyle {п _ { mathrm {D}}} ^ { mathrm {rand _degree}}}$ рассчитано Liu et al.^[2] примечательно. Если управляемость определяется в основном степенью, почему ${ Displaystyle {п _ { mathrm {D}}} ^ {настоящий}}$ и ${ Displaystyle {п _ { mathrm {D}}} ^ { mathrm {rand _degree}}}$ так отличается от многих реальных сетей? Они спорили ^[2] (arXiv: 1203.5161v1), что это могло быть связано с эффектом корреляции степеней. Однако было показано^[4] что управляемость сети может быть изменена только с помощью центральность посредственности и центральность близости, без использования степень (теория графов) или степени корреляции вообще.

Принципиальная схема показывает управление направленной сетью. Для заданной направленной сети (рис. А) вычисляется максимальное соответствие: наибольший набор ребер без общих головок или хвостов. Максимальное соответствие будет состоять из набора непересекающихся по вершинам направленных путей и направленных циклов (см. Красные края на рис. B). Если узел является головкой совпадающего ребра, то этот узел совпадает (зеленые узлы на рис. B). В противном случае он не совпадает (белые узлы на рис. B). Эти несогласованные узлы - это узлы, которыми нужно управлять, то есть узлы драйверов. Вводя сигналы в эти узлы драйвера, можно получить набор направленного пути, начальные точки которого являются входами (см. Рис. C). Эти пути называются «стеблями». Полученный орграф называется U-корневой факториальной связностью. «Прививая» направленные циклы к этим «стеблям», получаются «почки». Полученный орграф называется кактусом (см. Рис. D). Согласно теореме структурной управляемости^[5] поскольку существует структура кактусов, охватывающая контролируемую сеть (см. рис. e), система является управляемой. Структура кактусов (рис. D), лежащая в основе управляемой сети (рис. Е), является «скелетом» для поддержания управляемости.

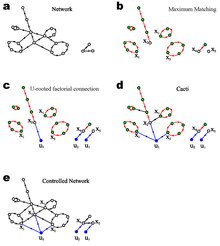
Структурная управляемость

Понятие структурных свойств было впервые введено Линем (1974).^[5] а затем расширен Шилдсом и Пирсоном (1976)^[6] и альтернативно получен Гловером и Сильверманом (1976).^[7] Главный вопрос заключается в том, является ли отсутствие управляемости или наблюдаемости общим в отношении переменных параметров системы. В рамках структурного управления параметрами системы являются либо независимые свободные переменные, либо фиксированные нули. Это согласуется с моделями физических систем, поскольку значения параметров никогда не известны точно, за исключением нулевых значений, которые выражают отсутствие взаимодействий или связей.

Максимальное соответствие

В теории графов соответствие - это множество ребер без общих вершин. Лю и др.^[2] расширил это определение до ориентированного графа, где соответствие - это набор ориентированных ребер, не имеющих общих начальных или конечных вершин. Легко проверить, что паросочетание ориентированного графа состоит из набора непересекающихся по вершинам простых путей и циклов. Максимальное согласование направленной сети можно эффективно вычислить, работая в двудольном представлении с использованием классического Алгоритм Хопкрофта-Карпа, который выполняется за O (E√N) время в худшем случае. Для неориентированного графа аналитические решения размера и количества максимальных соответствий были изучены с использованием полостной метод развит в статистической физике.^[8] Лю и др.^[2] расширил вычисления для ориентированного графа.

Вычисляя максимальное совпадение широкого диапазона реальных сетей, Liu et al.^[2] утверждал, что количество узлов драйвера определяется в основном распределением степени сети ${ Displaystyle P (к _ { mathrm {in}}, k _ { mathrm {out}})}$. Они также рассчитали среднее количество узлов драйверов для сетевого ансамбля с произвольным распределением степеней, используя полостной метод. Интересно, что для цепного графа и слабо плотно связного графа оба имеют очень разные внутренние и внешние распределения степеней; формулировка Liu et al.^[2] предсказал бы те же значения ${ Displaystyle {п _ { mathrm {D}}}}$. Кроме того, для многих сетей реального слова, а именно пищевых сетей, нейронных и метаболических сетей, несоответствие значений ${ Displaystyle {п _ { mathrm {D}}} ^ {настоящий}}$ и ${ Displaystyle {п _ { mathrm {D}}} ^ { mathrm {rand _degree}}}$ рассчитано Liu et al.^[2] примечательно. Если управляемость определяется исключительно степенью, почему ${ Displaystyle {п _ { mathrm {D}}} ^ {настоящий}}$ и ${ Displaystyle {п _ { mathrm {D}}} ^ { mathrm {rand _degree}}}$ так отличается от многих реальных сетей? Остается открытым для проверки, действительно ли надежность управления "в сетях больше зависит от использования центральность посредственности и центральность близости^[4] над степень (теория графов) метрики на основе.

Хотя более разреженные графики сложнее контролировать,^[2][4] очевидно было бы интересно узнать, центральность посредственности и центральность близости^[4] или степень неоднородности^[2] играет более важную роль в принятии решения об управляемости разреженных графов с почти одинаковыми распределениями степеней.

Управление составными квантовыми системами и алгебраическая теория графов

Теория управления сетями также была разработана в контексте универсального управления для составных квантовых систем, где подсистемы и их взаимодействия связаны с узлами и связями соответственно.^[9] Эта структура позволяет сформулировать критерий Калмана с помощью инструментов из алгебраическая теория графов через минимальный ранг графа и связанные с ним понятия.^[10][11]

Смотрите также

• Грамиан управляемости

Рекомендации

внешняя ссылка

• Сайт проекта сетевой управляемости
• Видео, демонстрирующее управляемость по сети