Алгебраическая теория графов - Algebraic graph theory

В высшей степени симметричный граф Граф Петерсена, который вершинно-транзитивный, симметричный, дистанционно-переходный, и дистанционно-регулярный. Она имеет диаметр 2. Его группа автоморфизмов имеет 120 элементов, и на самом деле симметричная группа ${ displaystyle S_ {5}}$.

Алгебраический теория графов это филиал математика в котором алгебраический методы применяются к проблемам о графики. Это в отличие от геометрический, комбинаторный, или алгоритмический подходы. Существует три основных раздела алгебраической теории графов, в которых используются линейная алгебра, использование теория групп, и изучение инварианты графа.

Разделы алгебраической теории графов

Использование линейной алгебры

Первая ветвь алгебраической теории графов включает изучение графов в связи с линейная алгебра. В частности, он изучает спектр из матрица смежности, или Матрица лапласа графа (эта часть алгебраической теории графов также называется спектральная теория графов ). Для Граф Петерсена, например, спектр матрицы смежности равен (−2, −2, −2, −2, 1, 1, 1, 1, 1, 3). Некоторые теоремы связывают свойства спектра с другими свойства графика. В качестве простого примера связанный график с диаметр D будет как минимум D+1 различные значения в его спектре.^[1] Аспекты спектров графов использовались при анализе синхронизируемость из сети.

Используя теорию групп

Вторая ветвь алгебраической теории графов включает изучение графов в связи с теория групп особенно группы автоморфизмов и геометрическая теория групп. Основное внимание уделяется различным семействам графов на основе симметрия (такие как симметричные графы, вершинно-транзитивные графы, реберно-транзитивные графы, дистанционно-транзитивные графы, дистанционно регулярные графы, и сильно регулярные графы ), и об отношениях включения между этими семьями. Некоторые из таких категорий графов достаточно разрежены, чтобы списки графиков можно составить. От Теорема Фрухта, все группы можно представить как группу автоморфизмов связного графа (действительно, кубический граф ).^[2] Другая связь с теорией групп состоит в том, что для любой группы симметричные графы, известные как Графики Кэли могут быть сгенерированы, и они имеют свойства, связанные со структурой группы.^[1]

А Граф Кэли для переменная группа А₄, образуя усеченный тетраэдр в трех измерениях. Все графики Кэли вершинно-транзитивный, но некоторые вершинно-транзитивные графы (например, Граф Петерсена ) не являются графами Кэли.

Правильная раскраска вершин Граф Петерсена с 3 цветами, минимально возможное количество. Согласно хроматический полином Всего 120 таких раскрасок по 3 цветам.

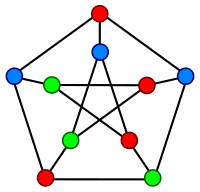
Эта вторая ветвь алгебраической теории графов связана с первой, поскольку свойства симметрии графа отражаются в его спектре. В частности, спектр высокосимметричного графа, такого как граф Петерсена, имеет несколько различных значений.^[1] (граф Петерсена имеет 3, что является минимально возможным с учетом его диаметра). Для графов Кэли спектр может быть напрямую связан со структурой группы, в частности с ее неприводимые персонажи.^[1][3]

Изучение инвариантов графов

Наконец, третья ветвь алгебраической теории графов касается алгебраических свойств инварианты графиков, и особенно хроматический полином, то Полином Тутте и инварианты узлов. Хроматический многочлен графа, например, считает количество его собственных раскраски вершин. Для графа Петерсена этот многочлен равен ${ Displaystyle т (т-1) (т-2) (т ^ {7} -12t ^ {6} + 67t ^ {5} -230t ^ {4} + 529t ^ {3} -814t ^ {2} + 775т-352)}$.^[1] В частности, это означает, что граф Петерсена не может быть правильно раскрашен в один или два цвета, но может быть раскрашен 120 различными способами в 3 цвета. Большая часть работ в этой области алгебраической теории графов была мотивирована попытками доказать теорема четырех цветов. Однако есть еще много открытые проблемы, например, характеризация графов с одним и тем же хроматическим полиномом и определение того, какие полиномы являются хроматическими.

Смотрите также

• Теория спектральных графов
• Алгебраическая комбинаторика
• Алгебраическая связность
• Разложение Дульмаджа – Мендельсона.
• Свойство графа
• Матрица смежности

использованная литература

внешние ссылки

• СМИ, связанные с Алгебраическая теория графов в Wikimedia Commons