Нелинейные эффекты - Википедия - Non-linear effects

Эта статья может быть слишком техническим для большинства читателей, чтобы понять. Пожалуйста помогите улучшить это к сделать понятным для неспециалистов, не снимая технических деталей. (Июнь 2014 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

В энантиоселективный синтез, нелинейный эффект относится к процессу, в котором энантиочистота катализатора или хиральный вспомогательный не соответствует энантиочистости производимого продукта. Например: a рацемический катализатор, как ожидается, превратит прохиральный субстрата в рацемический продукт (линейный эффект), но это не всегда так, и вместо него может быть получен хирально обогащенный продукт (нелинейный эффект).^[1][2]

Это можно выразить математически, как показано в уравнении 1. Стереоселекция, которая выше или ниже, чем энантиомерный избыток катализатора, считается неидеальным поведением. При неидеальном поведении это отклонение от линейности описывается как нелинейный эффект, NLE.^[3]

${ displaystyle ee _ { text {product}} = ee _ { max} ee _ { text {катализатор}}}$

Для идеального асимметричная реакция, ее_товар можно описать как продукт ее_{Максимум} умноженный на ее_{катализатор}. Это не относится к реакциям, проявляющим NLE.^[4]

Нелинейные эффекты часто возникают в реакциях с масштабной каталитической композицией.^[3] Как впервые было замечено Винбергом и Ферингой в 1976 году, различные энантиомеры хиральных катализаторов образуют гетерохиральные комплексы, более конкретно агрегаты высокого порядка или димерные формы катализатора.^[5] Эти гетерохиральные комплексы влияют на эффективное стереоиндукцию скалемического катализатора. Дополнительные источники нелинейных эффектов включают автокатализ, процесс, в котором реакция катализирует сама себя.^[6] Общие определения и математические модели являются ключом к пониманию нелинейных эффектов и их применения к конкретным химическим реакциям. В последние два десятилетия изучение нелинейных эффектов показало, что оно позволяет прояснить механизм реакции и направить в синтетических приложениях.

Типы нелинейных эффектов

Отношения между ээ_товар и ее_{катализатор} в сценариях (+) - NLE, linear и (-) - NLE.^[3]

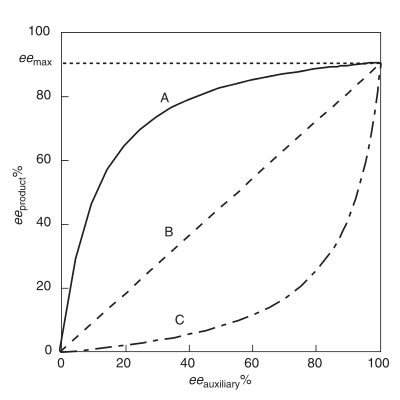
Положительный нелинейный эффект, (+) - NLE

А положительный нелинейный эффект, (+) - NLE, присутствует в асимметричной реакции, которая демонстрирует более высокий продукт ee (ee_товар ), чем предсказывается идеальной линейной ситуацией (Рисунок 1).^[4] Его часто называют асимметричное усиление, термин, введенный Огуни и его сотрудниками.^[4] Пример положительного нелинейного эффекта наблюдается в случае Шарплесса. эпоксидирование с подложкой гераниол.^[7] Во всех случаях химической реакционной способности, проявляющей (+) - NLE, существует врожденный компромисс между общей скоростью реакции и энантиоселективностью. Общая скорость ниже, а энантиоселективность выше по сравнению с линейной реакцией.

Отрицательный нелинейный эффект, (-) - NLE

Именуется как асимметричное истощение, присутствует отрицательный нелинейный эффект, когда ее_товар ниже, чем предсказывается идеальной линейной ситуацией.^[3] В отличие от (+) - NLE, (-) - NLE приводит к более высокой общей скорости реакции и снижению энантиоселективности. Синтетически эффект (-) - NLE может быть полезным при разумном анализе разделения энантиомеров продукта, и необходим высокий выход. Об интересном примере эффекта (-) - NLE сообщалось в асимметричном сульфиде. окисления.^[8]

Моделирование нелинейных эффектов

1n 1986 г., Анри Б. Каган и коллеги наблюдали серию известных реакций, которые следовали за неидеальным поведением. Поправочный коэффициент, ж, был адаптирован к уравнению 1, чтобы соответствовать кинетическому поведению реакций с NLE (уравнение 2).^[3]

${ displaystyle ee _ { text {product}} = f , ee _ { max} ee _ { text {катализатор}}}$

Уравнение 2: общее математическое уравнение, описывающее нелинейное поведение^[9]

К сожалению, уравнение 2 слишком общее, чтобы его можно было применять к конкретным химическим реакциям. В связи с этим Каган и его коллеги также разработали упрощенные математические модели для описания поведения катализаторов, которые приводят к нелинейным эффектам.^[3] В этих моделях используется общий ML._п видов, на основе металл (M) связаны с n числом энантиомеров лиганды (L). Тип MLп Модель варьируется между асимметричными реакциями в зависимости от степени соответствия данным реакции. При точном моделировании NLE может прояснить механистический детали энантиоселективной каталитической реакции.^[8]

ML₂ модель

Общее описание

Простейшая модель для описания нелинейного эффекта - ML₂ модель включает металлическую систему (M) с двумя хиральными лигандами, L_р и я_S. Помимо интересующей катализируемой реакции, модель учитывает установившееся равновесие между несвязанными и связанными каталитическими комплексами.^[3] В равновесии существуют три возможных каталитических комплекса (ML_SL_р, Мл_SL_S, Мл_рL_р). Два энантиомерно чистых комплекса (ML_SL_S, Мл_рL_р) называются гомохиральные комплексы.^[3] Возможный гетерохиральный комплекс, Мл_рL_S, часто называют мезо-комплексом.^[3]

Базовая схема МЛ₂ модель, разработанная Х. Б. Каганом ^[8]

В константа равновесия который описывает это равновесие, K, предположительно не зависит от каталитической химической реакции. В модели Кагана K определяется количеством агрегации, присутствующей в химической среде. K = 4 считается состоянием, при котором существует статистическое распределение лигандов для каждого металлического комплекса.^[3] Другими словами, нет термодинамический недостаток или преимущество образования гетерохиральных комплексов при K = 4.^[4]

Подчиняясь тому же кинетический По закону скорости каждый из трех каталитических комплексов катализирует желаемую реакцию с образованием продукта.^[8] Как энантиомеры друг друга, гомохиральные комплексы катализируют реакцию с одинаковой скоростью, хотя индуцируется противоположная абсолютная конфигурация продукта (т.е._RR= г_SS). Однако гетерохиральный комплекс образует рацемический продукт с другой константой скорости (т. е. r_RS).^[9]

Математическая модель для ML₂ Модель

Чтобы описать ML₂ Модель в количественных параметрах, Каган с сотрудниками описали следующую формулу:

${ displaystyle ee _ { text {product}} = ee _ { text {max}} ee _ { text {a вспомогательный}} (1+ beta) / (1 + g , beta)}$

В поправочный коэффициент Каган и его сотрудники ввели два новых параметра, отсутствующих в уравнении 1, β и g.^[9] В общем, эти параметры представляют собой концентрацию и активность трех каталитических комплексов относительно друг друга. β представляет собой относительное количество гетерохирального комплекса (ML_рL_S), как показано в уравнении 3.^[3] Важно понимать, что константа равновесия K не зависит ни от β, ни от g.^[8] Как описано Донна Блэкмонд в Научно-исследовательский институт Скриппса, "параметр K является неотъемлемым свойством каталитической смеси, не зависящим от ее_{катализатор}. K также не зависит от самой каталитической реакции и, следовательно, от параметра g ».

${ Displaystyle бета = г / (х + у)}$

Уравнение 3: Поправочный коэффициент β может быть описан как z, концентрация гетерохирального комплекса, деленная на x и y, соответствующие концентрации концентрации комплекса, деленные на x и y, соответствующие концентрации гомохиральных комплексов. ^[3]

Параметр g представляет реакционную способность гетерохирального комплекса по отношению к гомохиральным комплексам. Как показано в уравнении 5, это можно описать в терминах констант скорости. Поскольку гомохиральные комплексы реагируют с одинаковыми скоростями, g можно описать как константу скорости, соответствующую гетерохиральному комплексу, деленную на константу скорости, соответствующую любому гомохиральному комплексу.

${ displaystyle g = r_ {rs} / r_ {rr}}$

Уравнение 4: Параметр поправки g можно описать как скорость образования продукта с гетерохиральным катализатором ML_рL_S деленное на скорость образования продукта гомохирального комплекса (ML_рL_р или ML_SL_S).

Интерпретация математических результатов ML₂ Модель

• Если β = 0 или g = 1, ML₂ уравнение упрощается до уравнения 1. Мезокаталитический комплекс отсутствует или активен. Следовательно, простые аддитивные свойства должны применяться к такому сценарию, чтобы установить линейную взаимосвязь между энантиоселективностью продукта и энантиочистотой хирального катализатора.

• Если поправочный коэффициент больше единицы, реакция отображает асимметричное усиление, также известный как положительный нелинейный эффект. Под ML₂ Модель a (+) - NLE предполагает менее реактивный гетерохиральный катализатор. В этом случае константа равновесия K также увеличивается с увеличением поправочного коэффициента. Хотя энантиоселективность продукта относительно высока по сравнению с энантиоселективностью хирального катализатора, это происходит за счет общей скорости реакции. Чтобы достичь асимметричного усиления, должна быть относительно большая концентрация гетерохирального комплекса. Кроме того, этот гетерохиральный комплекс должен иметь значительно более низкую скорость реакции, r_RS. Следовательно, реакционноспособные каталитические частицы должны уменьшаться в концентрации, что приводит к общей более низкой скорости реакции.

• Если поправочный коэффициент меньше единицы, реакция отображает асимметричное истощение, также известный как отрицательный нелинейный эффект. В этом сценарии гетерохиральный катализатор относительно более реакционноспособен, чем гомохиральные каталитические комплексы. В этом случае (-) - NLE может привести к более быстрому, хотя и менее селективному образованию продукта.

iv. Кинетика реакции с ML₂ Модель: Вслед за Г. Публикация Каганом ML₂ Модель профессор Донна Блэкмонд из Скриппса продемонстрировала, как эту модель можно использовать для расчета общих скоростей реакции. С такими относительными скоростями реакции Блэкмонд показал, как ML₂ Модель может быть использована для формулирования кинетических прогнозов, которые затем можно будет сравнить с экспериментальными данными. Общее уравнение скорости, Уравнение 6, показано ниже.^[8]

${ displaystyle r = (x + y + gz) r_ {RR}}$

В дополнение к точности соответствия модели, кинетическая информация об общей реакции может дополнительно подтвердить предложенный механизм реакции. Например, положительный NLE в ML₂ должно привести к снижению общей скорости реакции.^[8] Решая скорость реакции из уравнения 6, можно подтвердить, так ли это.

M * L₂ Модель

Общее описание

Похож на ML₂ Согласно модели, эта модифицированная система включает хиральные лиганды, связывающиеся с металлическим центром (M), чтобы создать новый центр хиральности.^[4] В M * L есть четыре пары энантиомерных хиральных комплексов.₂ модель, как показано на рисунке 5.

Рисунок 5 Равновесие, присутствующее в M * L₂. Это очень похоже на ML.₂ модель. Однако из-за нового центра хиральности существует четыре набора энантиомеров.

В этой модели можно сделать приближение, что димерный комплексы необратимо диссоциируют на мономерный разновидность. В этом случае те же математические уравнения применяются к ML *₂ модель, которая применялась к ML₂ модель.

ML₃ модель

Общее описание

Более высокий уровень моделирования, ML₃ Модель включает четыре активных каталитических комплекса: ML_рL_рL_р, Мл_SL_SL_S, Мл_рL_рL_S, Мл_SL_SL_р. В отличие от ML₂ В модели, где только два гомохиральных комплекса прореагировали с образованием энантиомерно обогащенного продукта, все четыре каталитических комплекса реагируют энантиоселективно. Однако к равновесию между несвязанными и связанными каталитическими комплексами применимо то же предположение о стационарном состоянии, что и в более простом ML.₂ модель. Эта связь показана ниже на рисунке 7.

${ Displaystyle { ce {{M} + {L_ {R}} + L_ {S} <=>}} underbrace { ce {ML_ {R} L_ {R} L_ {R}}} _ { x} + underbrace { ce {ML_ {S} L_ {S} L_ {S}}} _ {y} + underbrace { ce {ML_ {R} L_ {R} L_ {S}}} _ { z} + underbrace { ce {ML_ {S} L_ {S} L_ {R}}} _ {w}}$

Рисунок 7: Равновесие между несвязанными частицами и реактивными каталитическими частицами в ML₃ модель.

Математическое моделирование

Расчет ее_товар значительно сложнее, чем в простом ML₂ модель. Каждый из двух гетерохиральных каталитических комплексов должен реагировать с одинаковой скоростью. Гомохиральные каталитические комплексы, подобные ML₂ случае, также должен реагировать с той же скоростью. Таким образом, поправочный параметр g по-прежнему рассчитывается как скорость гетерохирального каталитического комплекса, деленная на скорость гомохирального каталитического комплекса. Однако, поскольку гетерохиральные комплексы приводят к энантиомерно обогащенному продукту, общее уравнение для расчета ее_товар становится сложнее. На рисунке 8 показана математическая формула для расчета энантиоселективности.

${ displaystyle EE _ { text {prod}} = EE_ {0} ee _ { text {aux}} { frac {3 + 3 , g , EE '_ {0} / EE_ {0} + (1 -3 , g , EE '_ {0} / EE_ {0}) ee _ { text {aux}} ^ {2}} {1 + 3 , g + 3 (1-g) ee _ { text {aux}} ^ {2}}}}$

Рисунок 8: Математическая формула, описывающая машинное обучение₃ система. Ее_товар вычисляется путем умножения ее_{Максимум} поправочным коэффициентом, разработанным Каганом и соавторами.^[4]

Интерпретация ML₃ Модель

В общем, интерпретация значений параметра коррекции g для прогнозирования положительных и отрицательных нелинейных эффектов значительно сложнее. В случае, когда гетерохиральные комплексы ML_рL_рL_S и ML_SL_SL_р менее реактивны, чем гомохиральные комплексы ML_SL_SL_S и ML_рL_рL_р, кинетическое поведение аналогично ML₂ модель наблюдается (рисунок 9). Однако существенно иное поведение наблюдается в случае, когда гетерохиральные комплексы более реактивный чем гомохиральные комплексы.

Рисунок 9: Когда гетерохиральные комплексы более избирательны и реакционны, чем гомохиральные комплексы.^[4]

Рисунок 10: Когда гомохиральные комплексы более избирательны и реакционны, чем гетерохиральные комплексы.^[4]

Резервуарный эффект

Общее описание

Часто описывается рядом или в сотрудничестве с ML₂ В модели эффект резервуара описывает сценарий, в котором часть хирального лиганда выделяется пулу неактивных гетерохиральных каталитических комплексов вне каталитического цикла.^[4] Пул нереактивных гетерохиральных катализаторов, описанных с помощью ee_{бассейн}, достигает равновесия с каталитически активными гомохиральными комплексами, описываемыми с помощью ee_{эффективный}.^[8] В зависимости от концентрации неактивного пула катализаторов можно рассчитать энантиочистоту активных каталитических комплексов. Общий результат пластового эффекта - это асимметричное усиление, также известен как (+) - NLE.^[3]

Происхождение эффекта резервуара

Пул нереакционноспособных каталитических комплексов, описанный в эффекте резервуара, может быть результатом нескольких факторов. Одним из них потенциально может быть эффект агрегации гетерохиральных каталитических комплексов, который имеет место до установления равновесия в стационарном состоянии.^[3]

Ранние примеры нелинейного эффекта

Эпоксидирование гераниола по методу Sharpless

В 1986 году Каган и его сотрудники смогли продемонстрировать NLE с эпоксидированием по Шарплесу (E) -гераниола (рис. 11). В окислительных условиях Шарплесса с Ti (O-i-Pr)₄/ (+) - DET / t-BuOOH, Каган и его коллеги смогли продемонстрировать, что существует нелинейная корреляция между ее_товар и ее хирального катализатора, диэтилтартрата (DET).^[3] Как видно из рисунка 11, большее ее значение_товар чем ожидалось наблюдалось. Согласно ML₂ модели, Каган и его коллеги смогли сделать вывод, что присутствует менее реактивный гетерохиральный комплекс DET. Следовательно, это могло бы объяснить наблюдаемое асимметричное усиление. Данные NLE также согласуются с механизмом асимметричного эпоксидирования Шарплесса.^[10]

Рисунок 11: Общая схема реакции, изученная Каганом и его коллегами для эпоксидирования по Шарплесу гераниола.^[10]

Асимметричное окисление сульфидов

В 1994 году Каган и его коллеги сообщили о NLE в асимметричном окислении сульфидов. Степень соответствия данных реакции соответствует ML.₄ модель. Это означало, что димерный титан в комплексе с 4 лигандами DET был активным каталитическим веществом.^[3] В этом случае скорость реакции будет значительно выше по сравнению с идеальной кинетикой реакции. Недостатком, как и во всех (-) - сценариях NLE, является то, что энантиоселективность была ниже ожидаемой.^[3] Ниже, на Рисунке 12, можно увидеть, что вогнутость точек данных очень указывает на (-) - NLE.^[1]

Рисунок 12: Четкое указание на отрицательный нелинейный эффект в реакции асимметричного окисления сульфида.^[1]

Пребиотический катализ и нелинейный эффект

В пребиотическом химия, автокаталитический системы играют важную роль в понимании происхождения хиральности в жизни.^[6] Автокаталитическая реакция, реакция, в которой продукт действует как катализатор для самого себя, служит моделью для гомохиральность. Асимметричный Соаи реакция обычно называют химическим правдоподобием этой предбиотической гипотезы. В этой системе наблюдается асимметричное усиление в процессе автокаталитического катализа. Профессор Донна Блэкмонд подробно изучила НЭЭ этой реакции, используя ML Кагана.₂ модель. Из этого математического анализа Блэкмонд смог сделать вывод, что димерный гомохиральный комплекс является активным катализатором, способствующим гомохиральности реакции Соаи.^[3][6]

Примечания