Нелинейный фриктиофорез - Nonlinear frictiophoresis

Нелинейный фриктиофорез - однонаправленный дрейф частицы в среде, вызванный периодической движущей силой с нулевым средним. Эффект возможен из-за нелинейной зависимости силы трения-сопротивления от скорости частицы. Это было обнаружено теоретически.,^[1]и в основном известен как нелинейный электрофриктиофорез.^[1].^[2]На первый взгляд, периодическая движущая сила с нулевым средним значением способна вовлечь частицу в колебательное движение без однонаправленного дрейфа, потому что интегральный импульс, передаваемый частице силой, равен нулю. Возможность однонаправленного дрейфа можно распознать, если учесть, что частица сама теряет импульс, передавая его дальше той среде, в которой она движется. Если трение нелинейное, то может случиться так, что потеря количества движения при движении в одном направлении не будет равна потере импульса в противоположном направлении, и это вызовет однонаправленный дрейф. Чтобы это произошло, зависимость движущей силы от времени должна быть более сложной, чем в случае одной синусоидальной гармоники.

Простой пример - пластик Бингема

Нелинейное трение

Простейшим случаем закона зависимости трения от скорости являетсяСтокса один:

{ Displaystyle (1) qquad F_ {dr} (v) = лямбда v,}

куда ${ displaystyle F_ {dr} (v)}$ сила трения / сопротивления, приложенная к частице, движущейся со скоростью ${ displaystyle v}$ в среде. Закон трения-скорости (1) соблюдается для медленно движущейся сферической частицы в Ньютоновская жидкость.

Рис.1 Линейное трение

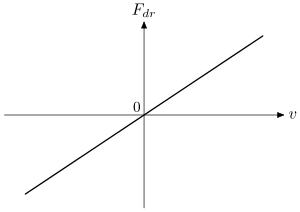
Он линейный, см. Рис. 1, и не подходит для проведения нелинейного фриктиофореза. Характерным свойством закона (1) является то, что любая, даже очень небольшая движущая сила способна заставить частицу двигаться. Это не относится к таким СМИ, как Бингем пластик. Для этих сред необходимо применить некоторую пороговую силу, ${ displaystyle d}$ , чтобы заставить частицу двигаться. Этот вид закона трения-скорости (сухое трение) имеет скачкообразный разрыв при ${ displaystyle v = 0}$ :

{ displaystyle (2) qquad F_ {dr} (v) = lambda v + d cdot mathrm {sign} (v).}

Рис.2 Пример нелинейного трения

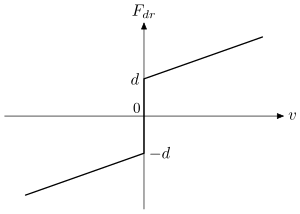
Он нелинейный, см. Рис. 2, и используется в этом примере.

Периодическая движущая сила

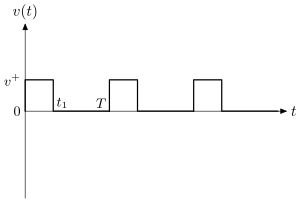
Позволять ${ displaystyle T> 0}$ обозначают период движущей силы. Выберите значение времени ${ displaystyle t_ {1}}$ такой, что ${ displaystyle 0$ и два значения силы, ${ displaystyle F ^ {+}> 0}$ , ${ Displaystyle F ^ {-} <0}$ такие, что удовлетворяются следующие отношения:

{ Displaystyle qquad qquad F ^ {+}> d, quad | F ^ {-} |

{ displaystyle (3) qquad F ^ {+} t_ {1} + F ^ {-} (T-t_ {1}) = 0.}

Периодическая движущая сила ${ displaystyle f (t)}$ в этом примере используется следующее:

{ displaystyle (4) qquad f (t) = { begin {cases} F ^ {+}, { text {if}} 0

Ясно, что в силу (3) ${ displaystyle f (t)}$ имеет нулевое среднее значение:

{ displaystyle int limits _ {0} ^ {T} f (t) dt = F ^ {+} t_ {1} + F ^ {-} (T-t_ {1}) = 0.}

Рис.3 Пример нулевой средней движущей силы

См. Также рис.3.

Однонаправленный дрейф

Для простоты мы рассматриваем здесь физическую ситуацию, когда инерцией можно пренебречь. Последнее может быть достигнуто, если масса частицы мала, скорость мала и трение велико. Эти условия должны гарантировать, что ${ displaystyle tau ll t_ {1}}$ ,куда ${ Displaystyle тау}$ время релаксации. В этой ситуации частица, движимая силой (4), сразу же начинает двигаться с постоянной скоростью ${ displaystyle v ^ {+} = { frac {1} { lambda}} (F ^ {+} - d)}$ во время интервала ${ Displaystyle 0 <т leq t_ {1}}$ и немедленно прекратит движение во время интервала ${ displaystyle t_ {1}$ см. рис.4.

Рис.4 Скорость с ненулевым средним

Это приводит к положительной средней скорости однонаправленного дрейфа:

{ displaystyle qquad qquad { overline {v (t)}} = { frac {1} {T}} int limits _ {0} ^ {T} v (t) dt = { frac { t_ {1}} { lambda T}} (F ^ {+} - d)> 0.}

Математический анализ

Проведен анализ возможности получения ненулевого дрейфа периодической силой с нулевым интегралом.^[1]Размерное уравнение движения частицы под действием периодической силы ${ displaystyle f (t)}$ , ${ Displaystyle е (т + 1) = е (т)}$ , ${ displaystyle int _ {0} ^ {1} f (t) dt = 0}$ как следует:

{ displaystyle (5) qquad { dot {v}} + lambda v- epsilon g (v) = f (t),}

где сила трения / сопротивления ${ Displaystyle F_ {dr} (v) = lambda v- epsilon g (v)}$ удовлетворяет следующему:

{ displaystyle qquad qquad F_ {dr} (- v) = - F_ {dr} (v), quad { frac {d} {dv}} F_ {dr} (v) geq 0.}

Это доказано в ^[1]что любое решение (5) переходит в периодический режим ${ Displaystyle v ^ {*} (т)}$ , ${ Displaystyle v ^ {*} (t + 1) = v ^ {*} (t)}$ , который имеет ненулевое среднее значение:

{ displaystyle qquad qquad { overline {v ^ {*} (t)}} = int limits _ {0} ^ {1} v ^ {*} (t) dt neq 0,}

почти наверняка при условии ${ displaystyle f (t)}$ не является антипериодическим.^[3]

За ${ Displaystyle г (v) = v ^ {3}}$ , два случая ${ displaystyle f (t)}$ были рассмотрены явно:

1. Пилообразная движущая сила, см. Рис. 5:

Рис.5 Пилообразная движущая сила

{ Displaystyle qquad qquad е (т) = ат, четырехъядерных т в [-1/2; 1/2], четырехъядерных е (т + 1) = е (т), четырехъядерных т в] - infty; infty [.}

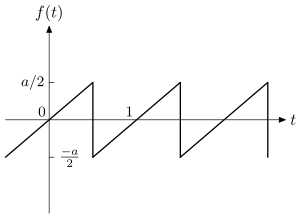
В этом случае найдено в ^[1]первый заказ в ${ displaystyle epsilon}$ приближение к ${ Displaystyle v ^ {*} (т)}$ , ${ Displaystyle v_ {1} ^ {*} (т)}$ , имеет следующее среднее значение:

{ Displaystyle qquad qquad { Big |} { overline {v_ {1} ^ {*} (t)}} { Big |} Equiv { Big |} int limits _ {0} ^ {1} v_ {1} ^ {*} (t) dt { Big |} geq { frac {2} {3}} epsilon a ^ {3} / lambda ^ {5}.}

Эта оценка сделана с расчетом ${ displaystyle lambda gg 1}$ .

2. Движущая сила двух гармоник,

{ displaystyle qquad qquad f (t) = a cos (2 pi t) + b cos (4 pi t + psi).}

В этом случае первый заказ в ${ displaystyle epsilon}$ приближение имеет следующее среднее значение:

{ displaystyle qquad qquad { Big |} { overline {v_ {1} ^ {*} (t)}} { Big |} = { Big |} int limits _ {0} ^ { 1} v_ {1} ^ {*} (t) dt { Big |} geq { frac {2} {27}} { frac { epsilon} { lambda}} left ({ frac { M} { lambda}} right) ^ {3} { frac {1} {(1 + { frac {4 pi ^ {2}} { lambda ^ {2}}}) (1+ { frac {16 pi ^ {2}} { lambda ^ {2}}}) ^ {1/2}}}.}

Это значение максимизируется в ${ displaystyle psi}$ , ${ displaystyle a, b}$ , сохраняя ${ displaystyle a + b = M}$ постоянный. Интересно, что величина дрейфа зависит от ${ displaystyle psi}$ и дважды меняет направление ${ displaystyle psi}$ охватывает интервал ${ displaystyle [0; 2 pi]}$ . Другой вид анализа,^[4] основанный на нарушении симметрии, также предполагает, что нулевое среднее значение движущей силы способно вызвать направленный дрейф.

Приложения

Рис.6 (а): сплошная линия - сила сопротивления заряда на одиночном о.п. от скорости, пунктирная линия - линейная аппроксимация для сравнения. (b): то же, что (a), но в мелком масштабе

В приложениях характер силы ${ displaystyle f (t)}$ в (5), обычно электрический, аналогичный силам, действующим при стандартном электрофорез. Единственное отличие состоит в том, что сила периодическая и без постоянной составляющей.

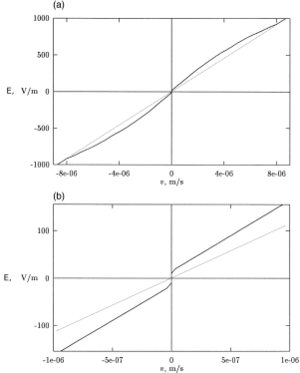
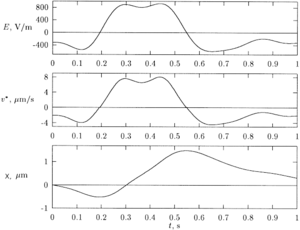
Чтобы эффект проявился, зависимость силы трения / сопротивления от скорости должна быть нелинейной. Это касается многих веществ, известных как неньютоновские жидкости. Среди них гели, и дилатантные жидкости, псевдопластические жидкости, жидкие кристаллы.^[5]Специальные эксперименты^[2]определили ${ displaystyle F_ {dr} (v)}$ для стандартной лестницы ДНК длиной до 1500 п.н. в 1,5% агарозном геле. Найденная зависимость, см. Рис. 6, подтверждает возможность нелинейного фриктиофореза в такой системе. Основываясь на данных на рис.6, оптимальное время для возбуждения электрического поля с нулевым средним значением, ${ displaystyle E (t)}$ , был найден в,^[2] что обеспечивает максимальный дрейф на 1500 б.п. длинный фрагмент, см. рис.7.

Рис.7 Динамика оптимального электрического поля,

{ displaystyle E (t)}

,

{ Displaystyle E (t pm 1s) = E (t)}

, установившаяся скорость,

{ Displaystyle v ^ {*} (т)}

, и смещение,

{ Displaystyle X (т)}

. Значение дрейфа

{ displaystyle { overline {v ^ {*} (t)}} = 0,31 mu}

РС.

Эффект однонаправленного дрейфа, вызванный периодической силой с нулевым интегральным значением, имеет своеобразную зависимость от времени действия приложенной силы. Примеры см. В предыдущем разделе. Это открывает новое измерение для ряда проблем разделения.

Разделение ДНК по длине

При разделении фрагментов ДНК периодическое электрическое поле с нулевым средним используется в электрофорезе с нулевым интегральным полем (ZIFE),^[6]где используется зависимость поля от времени, аналогичная показанной на рис. 3. Это позволяет разделить длинные фрагменты в агарозном геле, не разделенные стандартным электрофорезом в постоянном поле. Длинная геометрия ДНК и способ ее движения в геле, известный как отказ не позволяют применять непосредственно рассмотрение, основанное на формуле. (5), выше.

Разделение по удельной массе

Было замечено,^[7]что при определенных физических условиях механизм, описанный в разделе «Математический анализ» выше, может быть использован для разделения по удельной массе, как частицы, сделанные из изотопов одного и того же материала.

Расширения

Идея организации направленного дрейфа с периодическим приводом с нулевым средним получила дальнейшее развитие для других конфигураций и другого физического механизма нелинейности.

Вращение с помощью круговой волны

An электрический диполь свободно вращающийся вокруг ${ displaystyle z}$ -осью среды с нелинейным трением можно управлять, применяя электромагнитную волну, поляризованную по кругу вдоль ${ displaystyle pm z}$ и состоит из двух гармоник. Уравнение движения для этой системы следующее:

{ displaystyle qquad qquad { dot { omega}} + lambda omega - epsilon g ( omega) = f (t, theta (t)), quad { dot { theta}} = omega,}

куда ${ Displaystyle е (т, тета (т))}$ - крутящий момент, действующий на диполь из-за круговой волны:

{ displaystyle (6) qquad f (t, theta (t)) sim | p | (A_ {1} cos ( omega t pm theta) + A_ {2} cos (2 omega t pm theta + psi)),}

куда ${ displaystyle p}$ - составляющая дипольного момента, ортогональная ${ displaystyle z}$ ось ${ displaystyle theta}$ определяет направление диполя в ${ displaystyle XY}$ самолет. Выбрав правильный фазовый сдвиг ${ displaystyle psi}$ в (6) можно ориентировать диполь в любом желаемом направлении, ${ displaystyle theta _ {0}}$ .Направление ${ displaystyle theta _ {0}}$ достигается за счет направленного углового дрейфа, который обращается в ноль, когда ${ displaystyle theta = theta _ {0}}$ .^[8]^[9]Небольшая расстройка между первой и второй гармониками в (6) приводит к непрерывному вращательному дрейфу.^[9]

Модификация потенциальной функции

Рис.8 Пример модификации потенциальной функции

{ Displaystyle U (х)}

за счет нелинейного фриктиофореза. (а) начальный

{ Displaystyle U (х)}

, (б) модифицированный

{ Displaystyle U (х)}

.

Если частица совершает направленный дрейф при свободном движении в соответствии с формулой (5), то он дрейфует аналогично, если достаточно мелкое потенциальное поле ${ Displaystyle U (х)}$ навязывается. Уравнение движения в этом случае:

{ displaystyle qquad qquad { dot {v}} + lambda v- epsilon g (v) = f (t) - phi (x), quad { dot {x}} = v,}

куда ${ Displaystyle фи (х)}$ сила из-за потенциального поля. Дрейф продолжается до тех пор, пока не появится достаточно крутой участок в процессе ${ Displaystyle U (х)}$ встречается, что способно остановить занос. Такое поведение, как показывает строгий математический анализ, ^[10]приводит к модификации ${ Displaystyle U (х)}$ добавив линейный ${ displaystyle x}$ срок. Это может изменить ${ Displaystyle U (х)}$ качественно, например, изменение количества точек равновесия, см. рис. 8. Эффект может быть существенным при воздействии высокочастотного электрического поля на биополимеры. ^[11]

Другая нелинейность

За электрофорез коллоидных частиц под действием электрического поля малой напряженности, сила ${ displaystyle f (t)}$ в правой части уравнения. (5) линейно пропорциональна силе ${ displaystyle E (t)}$ приложенного электрического поля. При высокой напряженности линейность нарушается из-за нелинейной поляризации, в результате чего сила может нелинейно зависеть от приложенного поля:

{ displaystyle qquad qquad f (t) sim E (t) + alpha (E (t)) ^ {3}.}

В последнем выражении, даже если прикладное поле, ${ displaystyle E (t)}$ имеет нулевое среднее значение, приложенная сила ${ displaystyle f (t)}$ может иметь постоянную составляющую, которая может вызвать направленный дрейф.^[12]Как указано выше, чтобы это произошло, ${ displaystyle E (t)}$ должен иметь более одной синусоидальной гармоники. Такой же эффект для жидкости в трубке может служить вэлектроосмотический насос приводится в движение с нулевым средним электрическим полем.^[13]

Рекомендации

^ ^а ^б ^c ^d ^е Видибида Александр; Сериков, Александр (1985). «Электрофорез переменными полями в неньютоновской жидкости». Письма по физике. 108 (3): 170–172. Bibcode:1985ФЛА..108..170В. Дои:10.1016/0375-9601(85)90853-9.
^ ^а ^б ^c Видибида, А.К .; Erkızan, V .; Altungöz, O .; Челеби, Г. (2000). «Тестирование нелинейного электрофриктиофореза в агарозном геле». Биоэлектрохимия. 92: 91–101. Дои:10.1016 / S0302-4598 (00) 00088-X.
^ Функция ${ displaystyle f (t)}$ антипериодически, если для некоторых ${ displaystyle A}$ следующее соотношение ${ Displaystyle е (т + А) = - е (т)}$ относится ко всем ${ displaystyle t}$ . Индивидуальные гармоники, например ${ Displaystyle грех ( омега т)}$ , являются антипериодическими.
^ Nordén, B .; Золотарюк, Ю .; Christiansen, P.L .; Золотарюк, А. (2001). «Трещотка из-за нарушенной симметрии трения». Физический обзор E. 65 (1): 011110. Дои:10.1103 / PhysRevE.65.011110. PMID 11800680.Nordén, B .; Золотарюк, Ю .; Christiansen, P.L .; Золотарюк, А. (2002). «Храповое устройство с нарушенной симметрией трения». Письма по прикладной физике. 80 (14): 2601–2603. Bibcode:2002АпФЛ..80.2601Н. Дои:10.1063/1.1468900.
^ Simoff, D.A .; Портер, Р. (2011). «Реология и свойства термотропного жидко-кристаллического поли (бисфенола E изофталат-со-нафталат)». Молекулярные кристаллы и жидкие кристаллы. 110 (1–4): 1–26. Дои:10.1080/00268948408074493.
^ Noolandi, J .; Турмель, К. (1995). «Подготовка, манипуляции и импульсная стратегия для одномерного гель-электрофореза в импульсном поле (ODPFGE)». Мол Биотехнол. 4 (1): 25–43. Дои:10.1007 / BF02907469. PMID 8521038.
^ Видибида А. «Неопубликованные наблюдения». Цитировать журнал требует | журнал = (помощь)
^ Андрущенко, А.П .; Видибида, А. (1988). «Управление внутренним вращением в объектах молекулярного масштаба переменным пространственно-однородным электрическим полем». Автоматизация. 5: 58–61.
^ ^а ^б Видибида, А. (1999). «Глава 3 в:». Динамические механизмы воздействия переменных электромагнитных полей на макромолекулярные и кооперативные системы (PDF) (Докторская диссертация). Боголюбова. Институт теоретической физики.
^ Видибида, А. (1987). «Модификация потенциальной функции механической системы, вызванная периодическим действием». Советская физика.. 32: 113–115.Видибида, А. (1987). «Модификация потенциальной функции механической системы, вызванная периодическим действием». Acta Mechanica. 67 (1–4): 183–190. Дои:10.1007 / BF01182131.
^ Видибида, А. (1989). «Периодическое электрическое поле как переключатель конформации биополимера: возможный механизм». Eur Biophys J. 16 (6): 357–61. Дои:10.1007 / BF00257884. PMID 2924736.Видибида, А. (1999). «Глава 2 в:». Динамические механизмы воздействия переменных электромагнитных полей на макромолекулярные и кооперативные системы (PDF) (Докторская диссертация). Боголюбова. Институт теоретической физики.
^ Духин, С.С .; Видибида, А.К .; Духин, А.С .; Сериков, А.А. (1988). «Апериодический электрофорез. Направленный дрейф дисперсных частиц в однородном ангармоническом переменном электрическом поле». Коллоидный Ж. 49 (5): 752–755.Мищук, Н.А .; Баринова, Н. (2011). «Теоретическое и экспериментальное исследование нелинейного электрофореза». Коллоид J. 73: 88–96. Дои:10.1134 / S1061933X11010133.
^ Заявка США 20050129526, "Метод использования неуравновешенного переменного электрического поля в микрофлюидных устройствах", опубликовано 16 июня 2005 г., присвоено ДУХИНУ АНДРЕЮ С. и ДУХИНУ СТАНИСЛАВУ

[AlexanderVidybida1985-1] а ^б ^c ^d ^е Видибида Александр; Сериков, Александр (1985). «Электрофорез переменными полями в неньютоновской жидкости». Письма по физике. 108 (3): 170–172. Bibcode:1985ФЛА..108..170В. Дои:10.1016/0375-9601(85)90853-9.

[AlexanderVidybida2000-2] а ^б ^c Видибида, А.К .; Erkızan, V .; Altungöz, O .; Челеби, Г. (2000). «Тестирование нелинейного электрофриктиофореза в агарозном геле». Биоэлектрохимия. 92: 91–101. Дои:10.1016 / S0302-4598 (00) 00088-X.

[3] Функция ${ displaystyle f (t)}$ антипериодически, если для некоторых ${ displaystyle A}$ следующее соотношение ${ Displaystyle е (т + А) = - е (т)}$ относится ко всем ${ displaystyle t}$ . Индивидуальные гармоники, например ${ Displaystyle грех ( омега т)}$ , являются антипериодическими.

[Zolotaryuk2001-4] Nordén, B .; Золотарюк, Ю .; Christiansen, P.L .; Золотарюк, А. (2001). «Трещотка из-за нарушенной симметрии трения». Физический обзор E. 65 (1): 011110. Дои:10.1103 / PhysRevE.65.011110. PMID 11800680.Nordén, B .; Золотарюк, Ю .; Christiansen, P.L .; Золотарюк, А. (2002). «Храповое устройство с нарушенной симметрией трения». Письма по прикладной физике. 80 (14): 2601–2603. Bibcode:2002АпФЛ..80.2601Н. Дои:10.1063/1.1468900.

[Simoff2011-5] Simoff, D.A .; Портер, Р. (2011). «Реология и свойства термотропного жидко-кристаллического поли (бисфенола E изофталат-со-нафталат)». Молекулярные кристаллы и жидкие кристаллы. 110 (1–4): 1–26. Дои:10.1080/00268948408074493.

[Noolandi1995-6] Noolandi, J .; Турмель, К. (1995). «Подготовка, манипуляции и импульсная стратегия для одномерного гель-электрофореза в импульсном поле (ODPFGE)». Мол Биотехнол. 4 (1): 25–43. Дои:10.1007 / BF02907469. PMID 8521038.

[VidybidaUnp-7] Видибида А. «Неопубликованные наблюдения». Цитировать журнал требует | журнал = (помощь)

[Andr1988-8] Андрущенко, А.П .; Видибида, А. (1988). «Управление внутренним вращением в объектах молекулярного масштаба переменным пространственно-однородным электрическим полем». Автоматизация. 5: 58–61.

[DT-9] а ^б Видибида, А. (1999). «Глава 3 в:». Динамические механизмы воздействия переменных электромагнитных полей на макромолекулярные и кооперативные системы (PDF) (Докторская диссертация). Боголюбова. Институт теоретической физики.

[AlexanderVidybida1987-10] Видибида, А. (1987). «Модификация потенциальной функции механической системы, вызванная периодическим действием». Советская физика.. 32: 113–115.Видибида, А. (1987). «Модификация потенциальной функции механической системы, вызванная периодическим действием». Acta Mechanica. 67 (1–4): 183–190. Дои:10.1007 / BF01182131.

[AlexanderVidybida1989-11] Видибида, А. (1989). «Периодическое электрическое поле как переключатель конформации биополимера: возможный механизм». Eur Biophys J. 16 (6): 357–61. Дои:10.1007 / BF00257884. PMID 2924736.Видибида, А. (1999). «Глава 2 в:». Динамические механизмы воздействия переменных электромагнитных полей на макромолекулярные и кооперативные системы (PDF) (Докторская диссертация). Боголюбова. Институт теоретической физики.

[Dukhin1988-12] Духин, С.С .; Видибида, А.К .; Духин, А.С .; Сериков, А.А. (1988). «Апериодический электрофорез. Направленный дрейф дисперсных частиц в однородном ангармоническом переменном электрическом поле». Коллоидный Ж. 49 (5): 752–755.Мищук, Н.А .; Баринова, Н. (2011). «Теоретическое и экспериментальное исследование нелинейного электрофореза». Коллоид J. 73: 88–96. Дои:10.1134 / S1061933X11010133.

[DukhinPat-13] Заявка США 20050129526, "Метод использования неуравновешенного переменного электрического поля в микрофлюидных устройствах", опубликовано 16 июня 2005 г., присвоено ДУХИНУ АНДРЕЮ С. и ДУХИНУ СТАНИСЛАВУ

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]