Восьмигранная пирамида - Octahedral pyramid
| Восьмигранная пирамида | ||
|---|---|---|
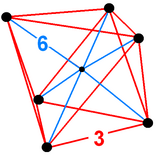
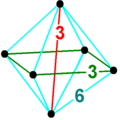
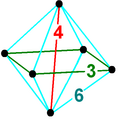
 Диаграмма Шлегеля | ||
| Тип | Многогранная пирамида | |
| Символ Шлефли | ( ) ∨ {3,4} () ∨ r {3,3} () ∨ s {2,6} ( ) ∨ [{4} + { }] ( ) ∨ [{ } + { } + { }] | |
| Клетки | 9 | 1 {3,4} 8 ( ) ∨ {3} |
| Лица | 20 {3} | |
| Края | 18 | |
| Вершины | 7 | |
| Двойной | Кубическая пирамида | |
| Группа симметрии | B3, [4,3,1], порядок 48 [3,3,1], порядок 24 [2+, 6,1], порядок 12 [4,2,1], порядок 16 [2,2,1], порядок 8 | |
| Характеристики | выпуклый, правильное лицо | |
В 4-х мерном геометрия, то восьмигранная пирамида ограничен одним октаэдр на базе и 8 треугольная пирамида клетки которые встречаются на вершине. Поскольку у октаэдра радиус описанной окружности, деленный на длину ребра, меньше единицы,[1] треугольные пирамиды можно сделать с правильными гранями (как правильные тетраэдры ) путем вычисления соответствующей высоты.
Появления восьмигранной пирамиды
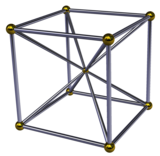
Регулярный 16 ячеек имеет восьмигранные пирамиды вокруг каждой вершины, с октаэдр проходящий через центр 16-кл. Таким образом, размещение двух правильных октаэдрических оснований пирамид в основании создает 16-элементную. 16-ячеечная мозаика 4-мерного пространства как 16-ячеечные соты.
Ровно 24 правильных восьмигранных пирамиды уместятся вокруг вершины в четырехмерном пространстве (вершина каждой пирамиды). Эта конструкция дает 24-элементный с октаэдрическими ограничивающими ячейками, окружающими центральную вершину с 24 длинными радиусами в длину ребра. 4-мерное содержимое 24-ячейки с единичной длиной ребра равно 2, поэтому содержимое правильной октаэдрической пирамиды равно 1/12. 24-ячеечная мозаика 4-мерного пространства как 24-ячеечные соты.
Восьмигранная пирамида - это вершина фигуры для усеченный 5-ортоплекс, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
График октаэдрической пирамиды - единственный возможный минимальный контрпример к Гипотеза Негами, что связные графы с плоские крышки сами являются проективно-планарными.[2]
Другие многогранники
Двойственная к восьмигранной пирамиде - это кубическая пирамида, рассматривается как кубическое основание и 6 квадратные пирамиды встреча в вершина.
Квадратно-пирамидальная пирамида
| Квадратно-пирамидальная пирамида | ||
|---|---|---|
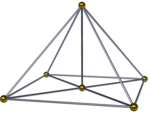 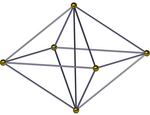 Диаграммы Шлегеля | ||
| Тип | Многогранная пирамида | |
| Символ Шлефли | ( ) ∨ [( ) ∨ {4}] [( )∨( )] ∨ {4} = { } ∨ {4} { } ∨ [{ } × { }] { } ∨ [{ } + { }] | |
| Клетки | 6 | 2 { } ∨ {4} 4 { } ∨ {3} |
| Лица | 12 {3} 1 {4} | |
| Края | 13 | |
| Вершины | 6 | |
| Двойной | Самодвойственный | |
| Группа симметрии | [4,1,1], порядок 8 [4,2,1], порядок 16 [2,2,1], порядок 8 | |
| Характеристики | выпуклый, правильное лицо | |
В квадратно-пирамидальная пирамида, () ∨ [() ∨ {4}], является пополам октаэдрической пирамидой. Оно имеет квадратная пирамида база и 4 тетраэдры вместе с еще одной квадратной пирамидой, сходящейся на вершине. Его также можно увидеть в проекции с центрированием по краям как квадратная бипирамида с четырьмя тетраэдрами, обернутыми вокруг общего ребра. Если высота двух вершин одинакова, ему можно присвоить имя более высокой симметрии [() ∨ ()] ∨ {4} = {} ∨ {4}, соединяющее ребро с перпендикулярным квадратом.[3]
В квадратно-пирамидальная пирамида можно превратить в прямоугольно-пирамидальная пирамида, {} ∨ [{} × {}] или ромбовидно-пирамидальная пирамида, {} ∨ [{} + {}] или другие формы более низкой симметрии.
В квадратно-пирамидальная пирамида существует как фигура вершины в однородных многогранниках вида ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , в том числе усеченный по битам 5-ортоплекс и усеченные тессерактические соты.
, в том числе усеченный по битам 5-ортоплекс и усеченные тессерактические соты.
Рекомендации
- ^ Клитцинг, Ричард. "3D выпуклые равномерные многогранники x3o4o - oct". 1 / sqrt (2) = 0,707 · 107
- ^ Глинены, Петр (2010), «20 лет гипотезе Негами о плоском покрытии» (PDF), Графы и комбинаторика, 26 (4): 525–536, CiteSeerX 10.1.1.605.4932, Дои:10.1007 / s00373-010-0934-9, МИСТЕР 2669457, S2CID 121645
- ^ Клитцинг, Ричард. «Сегментотоп скваск, К-4,4».
внешняя ссылка
- Ольшевский, Георгий. "Пирамида". Глоссарий по гиперпространству. Архивировано из оригинал 4 февраля 2007 г.
- Клитцинг, Ричард. «Сегментотопы 4D».
- Клитцинг, Ричард. «Сегментотоп октпий, К-4,3».
- Ричард Клитцинг, Осесимметричные грани равномерных многогранников.
| Этот 4-многогранник статья - это заглушка. Вы можете помочь Википедии расширяя это. |