Принцип ортогональности - Orthogonality principle

В статистика и обработка сигналов, то принцип ортогональности является необходимым и достаточным условием оптимальности Байесовская оценка. В общих чертах принцип ортогональности говорит, что вектор ошибок оптимальной оценки (в среднеквадратичная ошибка смысл) ортогонален любой возможной оценке. Принцип ортогональности чаще всего формулируется для линейных оценок, но возможны и более общие формулировки. Поскольку принцип является необходимым и достаточным условием оптимальности, его можно использовать для нахождения минимальная среднеквадратичная ошибка оценщик.

Принцип ортогональности для линейных оценок

Принцип ортогональности чаще всего используется при линейной оценке.^[1] В этом контексте пусть Икс быть неизвестным случайный вектор который должен быть оценен на основе вектора наблюдения у. Хочется построить линейную оценку ${displaystyle {hat {x}} = Hy + c}$ для какой-то матрицы ЧАС и вектор c. Тогда принцип ортогональности гласит, что оценка ${displaystyle {hat {x}}}$ достигает минимальная среднеквадратичная ошибка если и только если

${displaystyle operatorname {E} {({hat {x}} - x) y ^ {T}} = 0,}$ и
${displaystyle operatorname {E} {{hat {x}} - x} = 0.}$

Если Икс и у имеют нулевое среднее значение, тогда достаточно потребовать первого условия.

Пример

Предполагать Икс это Гауссовская случайная величина со средним м и дисперсия ${displaystyle sigma _ {x} ^ {2}.}$ Также предположим, что мы наблюдаем значение ${displaystyle y = x + w,}$ куда ш гауссов шум, не зависящий от Икс и имеет среднее значение 0 и дисперсию ${displaystyle sigma _ {w} ^ {2}.}$ Мы хотим найти линейную оценку ${displaystyle {hat {x}} = hy + c}$ минимизация MSE. Подставляя выражение ${displaystyle {hat {x}} = hy + c}$ в два требования принципа ортогональности, получаем

{displaystyle 0 = operatorname {E} {({hat {x}} - x) y}}

{displaystyle 0 = operatorname {E} {(hx + hw + c-x) (x + w)}}

{displaystyle 0 = h (sigma _ {x} ^ {2} + sigma _ {w} ^ {2}) + hm ^ {2} + cm-sigma _ {x} ^ {2} -m ^ {2} }

и

{displaystyle 0 = operatorname {E} {{hat {x}} - x}}

{displaystyle 0 = operatorname {E} {hx + hw + c-x}}

{displaystyle 0 = (h-1) m + c.}

Решая эти два линейных уравнения относительно час и c приводит к

{displaystyle h = {frac {sigma _ {x} ^ {2}} {sigma _ {x} ^ {2} + sigma _ {w} ^ {2}}}, quad c = {frac {sigma _ {w } ^ {2}} {сигма _ {x} ^ {2} + сигма _ {w} ^ {2}}} м,}

так что линейная оценка минимальной среднеквадратичной ошибки задается

{displaystyle {hat {x}} = {frac {sigma _ {x} ^ {2}} {sigma _ {x} ^ {2} + sigma _ {w} ^ {2}}} y + {frac {sigma _ {w} ^ {2}} {sigma _ {x} ^ {2} + sigma _ {w} ^ {2}}} m.}

Эту оценку можно интерпретировать как средневзвешенное значение измерений зашумленных измерений. у и предыдущее ожидаемое значение м. Если дисперсия шума ${displaystyle sigma _ {w} ^ {2}}$ низка по сравнению с дисперсией предыдущего ${displaystyle sigma _ {x} ^ {2}}$ (соответствует высокому SNR ), то большая часть веса приходится на измерения у, которые считаются более надежными, чем предыдущая информация. И наоборот, если дисперсия шума относительно выше, то оценка будет близка к м, поскольку измерения недостаточно надежны, чтобы перевесить предварительную информацию.

Наконец, обратите внимание, что поскольку переменные Икс и у вместе являются гауссовыми, оценка минимальной MSE линейна.^[2] Следовательно, в этом случае описанный выше оценщик минимизирует MSE среди всех оценщиков, а не только для линейных оценщиков.

Общая формулировка

Позволять ${displaystyle V}$ быть Гильбертово пространство случайных величин с внутренний продукт определяется ${displaystyle langle x, yangle = имя оператора {E} {x ^ {H} y}}$ . Предполагать ${displaystyle W}$ это закрыто подпространство ${displaystyle V}$ , представляющий пространство всех возможных оценок. Хочется найти вектор ${displaystyle {hat {x}} на W}$ который аппроксимирует вектор ${displaystyle xin V}$ . Точнее, хотелось бы минимизировать среднеквадратичную ошибку (MSE). ${displaystyle operatorname {E} | x- {шляпа {x}} | ^ {2}}$ между ${displaystyle {hat {x}}}$ и ${displaystyle x}$ .

В частном случае линейных оценок, описанном выше, пространство ${displaystyle V}$ это набор всех функций ${displaystyle x}$ и ${displaystyle y}$ , пока ${displaystyle W}$ - множество линейных оценок, т. е. линейных функций от ${displaystyle y}$ Только. Другие параметры, которые можно сформулировать таким образом, включают подпространство причинный линейные фильтры и подпространство всех (возможно, нелинейных) оценок.

Геометрически мы можем увидеть эту проблему в следующем простом случае, когда ${displaystyle W}$ это одномерный подпространство:

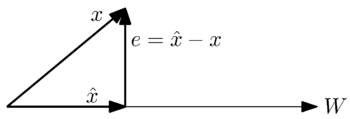
Мы хотим найти наиболее близкое приближение к вектору ${displaystyle x}$ вектором ${displaystyle {hat {x}}}$ в пространстве ${displaystyle W}$ . Из геометрической интерпретации интуитивно понятно, что наилучшее приближение или наименьшая ошибка возникает, когда вектор ошибки ${displaystyle e}$ , ортогональна векторам в пространстве ${displaystyle W}$ .

Точнее, общий принцип ортогональности утверждает следующее: для замкнутого подпространства ${displaystyle W}$ оценок в гильбертовом пространстве ${displaystyle V}$ и элемент ${displaystyle x}$ в ${displaystyle V}$ , элемент ${displaystyle {hat {x}} на W}$ достигает минимальной MSE среди всех элементов в ${displaystyle W}$ если и только если ${displaystyle operatorname {E} {(x- {hat {x}}) y ^ {T}} = 0}$ для всех ${displaystyle yin W.}$

Сформулированный таким образом, этот принцип является просто утверждением Теорема проекции Гильберта. Тем не менее, широкое использование этого результата в обработке сигналов привело к названию «принцип ортогональности».

Решение проблем минимизации ошибок

Ниже приводится один из способов найти минимальная среднеквадратичная ошибка оценка с использованием принципа ортогональности.

Мы хотим иметь возможность аппроксимировать вектор ${displaystyle x}$ к

{displaystyle x = {hat {x}} + e,}

куда

{displaystyle {hat {x}} = sum _ {i} c_ {i} p_ {i}}

это приближение ${displaystyle x}$ как линейная комбинация векторов из подпространства ${displaystyle W}$ охватывает ${displaystyle p_ {1}, p_ {2}, ldots.}$ Поэтому мы хотим иметь возможность найти коэффициенты, ${displaystyle c_ {i}}$ , так что мы можем записать наше приближение в известных терминах.