Лемма восходящего солнца - Википедия - Rising sun lemma

Иллюстрация, объясняющая, почему эта лемма называется «леммой о восходящем солнце».

В математический анализ, то лемма восходящего солнца это лемма из-за Фриджес Рис, использованный в доказательстве Максимальная теорема Харди – Литтлвуда.. Лемма была предвестником в одном измерении Лемма Кальдерона – Зигмунда..^[1]

Лемма формулируется следующим образом.^[2]

Предполагать грамм - вещественнозначная непрерывная функция на интервале [а,б] и S это набор Икс в [а,б] такое, что существует y∈(Икс,б] с грамм(y) > грамм(Икс). (Обратите внимание, что б не может быть в S, хотя а может быть.) Определить E = S ∩ (а,б).

потом E является открытым множеством, и его можно записать как счетное объединение непересекающихся интервалов

${ displaystyle E = bigcup _ {k} (a_ {k}, b_ {k})}$

такой, что грамм(а_k) = грамм(б_k), пока не а_k = а ∈ S для некоторых k, в таком случае грамм(а) < грамм(б_k) для этого k. Кроме того, если Икс ∈ (а_k,б_k), тогда грамм(Икс) < грамм(б_k).

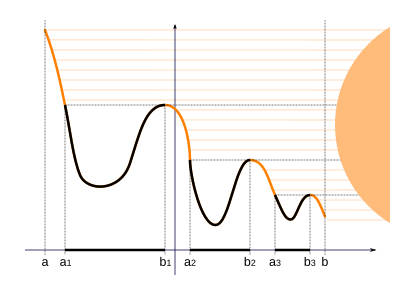
Красочное название леммы связано с представлением графика функции грамм как горный пейзаж, где солнце светит горизонтально справа. Набор E состоят из точек, находящихся в тени.

Доказательство

Нам понадобится лемма: предположим [c,d) ⊂ S, но d ∉ S. потом грамм(c) < грамм(d). Для доказательства предположим грамм(c) ≥ грамм(d).Потом грамм достигает максимума на [c,d] в какой-то момент z < d.С z ∈ S, Существует y в (z,б] с грамм(z) < грамм(y). Если y ≤ d, тогда грамм не достигнет максимума на [c,d] в z.Таким образом, y ∈ (d,б], и грамм(d) ≤ грамм(z) < грамм(y).Это означает, что d ∈ SПротиворечие, доказывающее лемму.

Набор E открыто, поэтому состоит из счетного объединения непересекающихся интервалов (а_k,б_k).

Из леммы сразу следует, что грамм(Икс) < грамм(б_k) за Икс в (а_k,б_k).С грамм непрерывно, мы также должны иметь грамм(а_k) ≤ грамм(б_k).

Если а_k ≠ а или же а ∉ S, тогда а_k ∉ S, так грамм(а_k) ≥ грамм(б_k), иначе а_k ∈ S. Таким образом, грамм(а_k) = грамм(б_k) в этих случаях.

Наконец, если а_k = а ∈ S, лемма говорит нам, что грамм(а) < грамм(б_k).

Примечания

Рекомендации

• Дурен, Питер Л. (2000), Теория H^п Пространства, Нью-Йорк: Dover Publications, ISBN  0-486-41184-2
• Гарлинг, Д.Дж. (2007), Неравенства: путь к линейному анализу, Издательство Кембриджского университета, ISBN  978-0-521-69973-0
• Кореновский, А. А .; А. К. Лернер; А. М. Стоколос (ноябрь 2004 г.), «О многомерной форме леммы Ф. Рисса о« восходящем солнце »», Труды Американского математического общества, 133 (5): 1437–1440, Дои:10.1090 / S0002-9939-04-07653-1
• Рис, Фредерик (1932), "Sur un Théorème de Maximum de Mm. Hardy et Littlewood", Журнал Лондонского математического общества, 7 (1): 10–13, Дои:10.1112 / jlms / s1-7.1.10, получено 2008-07-21
• Штейн, Элиас (1998), «Сингулярные интегралы: роль Кальдерона и Зигмунда» (PDF), Уведомления Американского математического общества, 45 (9): 1130–1140.
• Тао, Теренс (2011), Введение в теорию меры, Аспирантура по математике, 126, Американское математическое общество, ISBN  978-0821869192
• Зигмунд, Антони (1977), Тригонометрический ряд. Vol. I, II (2-е изд.), Cambridge University Press, ISBN  0-521-07477-0