Чувствительность (системы управления) - Sensitivity (control systems)

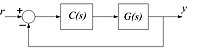
Базовая система управления с обратной связью, использующая единичную отрицательную обратную связь. C (s) и G (s) обозначают передаточные функции компенсатора и объекта соответственно.

Параметры контроллера обычно соответствуют процесс характеристики и поскольку процесс может измениться, важно, чтобы параметры регулятора были выбраны таким образом, чтобы замкнутый цикл Система нечувствительна к изменениям в динамике процесса. Один из способов охарактеризовать чувствительность - через номинальный пик чувствительности. ${ displaystyle M_ {s}}$ :^[1]

${ displaystyle M_ {s} = max _ {0 leq omega < infty} left | S (j omega) right | = max _ {0 leq omega < infty} left | { frac {1} {1 + G (j omega) C (j omega)}} right |}$

куда ${ Displaystyle G (s)}$ и ${ Displaystyle C (s)}$ обозначают передаточную функцию объекта и контроллера в базовой системе управления с обратной связью с использованием единичной отрицательной обратной связи.

Функция чувствительности ${ displaystyle S}$ , которая появляется в приведенной выше формуле, также описывает передаточную функцию от внешнего возмущения к выходу процесса. Фактически, если допустить аддитивное возмущение п после вывода

Блок-схема системы управления с возмущением

установки передаточные функции замкнутой системы задаются выражением

${ Displaystyle Y (s) = { гидроразрыва {C (s) G (s)} {1 + C (s) G (s)}} R (s) + { frac {1} {1 + C ( s) G (s)}} N (s)}$

Следовательно, более низкие значения ${ displaystyle | S |}$ предложить дальнейшее ослабление внешнего возмущения. Функция чувствительности сообщает нам, как обратная связь влияет на помехи. Помехи с такими частотами, что ${ displaystyle | S (j omega) |}$ меньше единицы уменьшаются на величину, равную расстоянию до критической точки ${ displaystyle -1}$ и возмущения с такими частотами, что ${ displaystyle | S (j omega) |}$ больше единицы, усиливаются обратной связью.^[2]

Важно, чтобы максимальное значение функции чувствительности было ограничено для системы управления, и обычно требуется, чтобы максимальное значение функции чувствительности, ${ displaystyle M_ {s}}$ , быть в диапазоне от 1,3 до 2.

Круг чувствительности

Количество ${ displaystyle M_ {s}}$ является обратной величиной кратчайшего расстояния от Кривая Найквиста передаточной функции петли до критической точки ${ displaystyle -1}$ . Чувствительность ${ displaystyle M_ {s}}$ гарантирует, что расстояние от критической точки до кривой Найквиста всегда больше, чем ${ displaystyle { frac {1} {M_ {s}}}}$ а кривая Найквиста петлевой передаточной функции всегда находится вне круга вокруг критической точки ${ displaystyle -1 + 0j}$ с радиусом ${ displaystyle { frac {1} {M_ {s}}}}$ , известный как круг чувствительности. ${ displaystyle M_ {s}}$ определяет максимальное значение функции чувствительности и инверсию ${ displaystyle M_ {s}}$ дает вам кратчайшее расстояние от передаточной функции без обратной связи ${ displaystyle L (j omega)}$ до критической точки ${ displaystyle -1 + 0j}$ .^[3]^[4]