ПИД-регулятор - PID controller
А пропорционально-интегрально-производный регулятор (ПИД-регулятор или же трехчленный контролер) это контур управления механизм, использующий Обратная связь который широко используется в системы промышленного управления и множество других приложений, требующих непрерывно модулируемого управления. ПИД-регулятор постоянно вычисляет значение ошибки как разница между желаемым уставка (SP) и измеренная переменная процесса (PV) и применяет поправку на основе пропорциональный, интеграл, и производная термины (обозначены п, я, и D соответственно), отсюда и название.
На практике он автоматически применяет точную и отзывчивую коррекцию к функции управления. Повседневный пример - это круиз-контроль на автомобиле, где подъем на холм снизит скорость, если будет применяться только постоянная мощность двигателя. Алгоритм ПИД-регулятора восстанавливает измеренную скорость до желаемой скорости с минимальной задержкой и выбросом за счет увеличения выходной мощности двигателя.
Первый теоретический анализ и практическое применение были в области систем автоматического рулевого управления для судов, разработанных с начала 1920-х годов. Затем он использовался для автоматического управления процессами в обрабатывающей промышленности, где он широко применялся в пневматике, а затем в электронике, контроллеры. Сегодня концепция PID повсеместно используется в приложениях, требующих точного и оптимизированного автоматического управления.
Фундаментальная операция

Отличительной особенностью ПИД-регулятора является возможность использования трех условия контроля пропорционального, интегрального и производного воздействия на выход контроллера для обеспечения точного и оптимального управления. На блок-схеме справа показаны принципы создания и применения этих терминов. Он показывает ПИД-регулятор, который непрерывно вычисляет значение ошибки как разница между желаемым уставка и размеренный переменная процесса : , и применяет поправку на основе пропорциональный, интеграл, и производная термины. Контроллер пытается минимизировать ошибку с течением времени, регулируя управляющая переменная , например, открытие регулирующий вентиль, к новому значению, определяемому взвешенная сумма условий контроля.
В этой модели:
- Срок п пропорциональна текущему значению ошибки SP - PV . Например, если ошибка большая и положительная, управляющий выходной сигнал будет пропорционально большим и положительным с учетом коэффициента усиления «K». Использование одного только пропорционального управления приведет к ошибке между заданным значением и фактическим значением процесса, потому что для создания пропорционального отклика требуется ошибка. Если ошибки нет, нет и корректирующего ответа.
- Срок я учитывает прошлые значения ошибки SP - PV и интегрирует их с течением времени для получения я срок. Например, если есть остаточная ошибка SP - PV после применения пропорционального управления, интегральный член стремится устранить остаточную ошибку, добавляя управляющий эффект из-за исторического кумулятивного значения ошибки. Когда ошибка будет устранена, интегральный член перестанет расти. Это приведет к уменьшению пропорционального эффекта по мере уменьшения ошибки, но это компенсируется растущим интегральным эффектом.
- Срок D является наилучшей оценкой будущей тенденции ошибки SP - PV, основанной на ее текущей скорости изменения. Иногда его называют «упреждающим контролем», поскольку он эффективно направлен на уменьшение влияния ошибки SP - PV путем оказания управляющего воздействия, создаваемого скоростью изменения ошибки. Чем быстрее изменение, тем больше регулирующий или демпфирующий эффект.[1]
Тюнинг - Баланс этих эффектов достигается за счет настройка петли для получения оптимальной функции управления. Константы настройки показаны ниже как «K» и должны быть получены для каждого приложения управления, поскольку они зависят от характеристик отклика всего контура, внешнего по отношению к контроллеру. Они зависят от поведения измерительного датчика, конечного элемента управления (например, регулирующего клапана), любых задержек управляющего сигнала и самого процесса. Приблизительные значения констант обычно могут быть изначально введены, зная тип приложения, но обычно они уточняются или настраиваются путем «ускорения» процесса на практике путем введения изменения уставки и наблюдения за реакцией системы.
Управляющее действие - Математическая модель и практический цикл, описанные выше, используют «прямое» управляющее воздействие для всех членов, что означает, что увеличение положительной ошибки приводит к увеличению выходного положительного управляющего сигнала для суммированных членов для применения коррекции. Однако выход называется «обратным» действием, если необходимо применить отрицательное корректирующее действие. Например, если клапан в контуре потока открывался на 100–0% для управляющего выхода 0–100% - это означает, что действие контроллера должно быть отменено. Некоторые схемы управления технологическим процессом и конечные элементы управления требуют этого обратного действия. Примером может служить клапан для охлаждающей воды, где безотказный режим, в случае потери сигнала, будет 100% открытие клапана; поэтому 0% выходного сигнала контроллера должен вызвать 100% открытие клапана.
Математическая форма
Общая функция контроля
куда , , и , все неотрицательные, обозначим коэффициенты при пропорциональный, интеграл, и производная термины соответственно (иногда обозначаются п, я, и D).
в стандартная форма уравнения (см. далее в статье), и соответственно заменяются на и ; Преимущество этого в том, что и имеют некоторый понятный физический смысл, поскольку представляют время интегрирования и время производной соответственно.
Выборочное использование контрольных терминов
Хотя у ПИД-регулятора есть три элемента управления, в некоторых приложениях требуется только один или два элемента для обеспечения соответствующего управления. Это достигается установкой неиспользуемых параметров на ноль и называется контроллером PI, PD, P или I при отсутствии других управляющих воздействий. ПИ-регуляторы довольно распространены в приложениях, в которых действие по производной будет чувствительно к шуму измерения, но интегральный член часто необходим для того, чтобы система достигла целевого значения.
Применимость
Использование алгоритма PID не гарантирует оптимальный контроль системы или ее стабильность управления . Могут возникнуть ситуации, когда возникают чрезмерные задержки: измерение значения процесса задерживается или управляющее воздействие применяется недостаточно быстро. В этих случаях компенсация опережения и запаздывания требуется, чтобы быть эффективным. Реакцию контроллера можно описать с точки зрения его реакции на ошибку, степени, в которой система промахи уставка и степень любой системы колебание. Но ПИД-регулятор широко применим, поскольку он полагается только на реакцию измеряемой переменной процесса, а не на знания или модель базового процесса.
История


Происхождение
Непрерывное управление до того, как ПИД-регуляторы были полностью поняты и реализованы, одним из источников является центробежный регулятор, который использует вращающиеся веса для управления процессом. Это было изобретено Кристиан Гюйгенс в 17 веке, чтобы урегулировать разрыв между жернова в ветряные мельницы в зависимости от скорости вращения, и тем самым компенсировать переменную скорость подачи зерна.[2][3]
С изобретением стационарного парового двигателя низкого давления возникла необходимость в автоматическом регулировании скорости, и Джеймс Ватт Самостоятельно спроектированный регулятор «конического маятника», набор вращающихся стальных шариков, прикрепленных к вертикальному шпинделю с помощью рычагов, стал промышленным стандартом. Это было основано на концепции контроля зазора между жерновами.[4]
Однако регулирование скорости вращения с помощью регулятора скорости оставалось переменным в условиях изменяющейся нагрузки, где был очевиден недостаток того, что сейчас известно как пропорциональное регулирование. Ошибка между желаемой скоростью и фактической скоростью будет увеличиваться с увеличением нагрузки. В XIX веке теоретические основы деятельности губернаторов впервые описал Джеймс Клерк Максвелл в 1868 г. в своей теперь известной работе О губернаторах. Он исследовал математические основы устойчивости управления и продвинулся в поисках решения, но призвал математиков изучить проблему.[5][4] Проблема была дополнительно исследована в 1874 г. Эдвард Раут, Чарльз Штурм, а в 1895 г. Адольф Гурвиц все они внесли свой вклад в установление критериев устойчивости управления.[4]В последующих приложениях регуляторы скорости были доработаны, в частности, американскими учеными. Уиллард Гиббс, который в 1872 году теоретически проанализировал конический маятниковый регулятор Ватта.
Примерно в это время изобретение Торпеда Уайтхеда возникла проблема управления, требующая точного контроля глубины спуска. Использование только датчика давления глубины оказалось недостаточным, и маятник, который измерял продольный и поперечный наклон торпеды, был объединен с измерением глубины, чтобы стать маятниково-гидростатическое управление. Регулирование давления обеспечивало только пропорциональное регулирование, которое при слишком высоком усилении регулирования становилось нестабильным и выходило за пределы допустимого диапазона. нестабильность глубины удержания. Маятник добавил то, что теперь известно как производное управление, которое гасит колебания, определяя угол пикирования / набора высоты торпеды и тем самым скорость изменения глубины.[6] Эта разработка (названная Уайтхедом «Секретом», чтобы не объяснить ее действия) произошла примерно в 1868 году.[7]
Другой ранний пример ПИД-регулятора был разработан Элмер Сперри в 1911 году для управления кораблем, хотя его работа была интуитивной, а не математической.[8]
Однако только в 1922 году формальный закон управления для того, что мы сейчас называем ПИД-регулятором, или трехчленным управлением, был впервые разработан с использованием теоретического анализа. Русский американец инженер Николас Минорский.[9] Минорский занимался исследованиями и проектированием системы автоматического управления кораблем для ВМС США и основывал свой анализ на наблюдениях за рулевой. Он отметил, что рулевой управлял кораблем, основываясь не только на текущей ошибке курса, но и на прошлой ошибке, а также на текущей скорости изменения;[10] Затем Минорский дал ему математическую трактовку.[4]Его целью была стабильность, а не общий контроль, что значительно упростило задачу. Хотя пропорциональное управление обеспечивало устойчивость к небольшим возмущениям, его было недостаточно для борьбы с устойчивыми возмущениями, особенно с сильным штормом (из-за установившаяся ошибка ), что потребовало добавления интегрального члена. Наконец, для улучшения стабильности и контроля был добавлен производный член.
Испытания проводились на USS Нью-Мексико, с контроллерами, управляющими угловая скорость (не угол) руля направления. ПИ-регулирование давало устойчивый рыскание (угловая погрешность) ± 2 °. Добавление элемента D дало ошибку по рысканью ± 1/6 °, что лучше, чем может достичь большинство рулевых.[11]
В конечном итоге ВМС не приняли эту систему из-за сопротивления личного состава. Аналогичная работа была проведена и опубликована несколькими другими в 1930-х годах.
Промышленный контроль
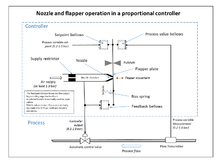
Широкое использование контроллеров обратной связи не стало возможным до тех пор, пока не были разработаны широкополосные усилители с высоким коэффициентом усиления, использующие концепцию отрицательной обратной связи. Это было разработано в телефонной инженерной электронике Гарольд Блэк в конце 1920-х, но не публиковался до 1934 года.[4] Независимо, Клессон Э. Мейсон из компании Foxboro в 1930 году изобрел широкополосный пневматический контроллер, объединив сопло и заслонка Пневматический усилитель с высоким коэффициентом усиления, изобретенный в 1914 году, с отрицательной обратной связью с выхода контроллера. Это резко увеличило линейный диапазон работы усилителя сопла и заслонки, а также можно было бы добавить интегральное управление за счет использования прецизионного спускного клапана и сильфона, генерирующего интегральный член. Результатом стал контроллер «Stabilog», который давал как пропорциональные, так и интегральные функции с помощью сильфона обратной связи.[4] Интегральный член был назван Перезагрузить.[12] Позже к производному члену добавился дополнительный сильфон и регулируемое отверстие.
Примерно с 1932 года использование широкополосных пневматических контроллеров быстро увеличивалось в различных приложениях управления. Давление воздуха использовалось для генерации выходного сигнала контроллера, а также для питания устройств регулирования процесса, таких как диафрагменные. регулирующие клапаны. Это были простые устройства, не требующие особого обслуживания, которые хорошо работали в суровых промышленных условиях и не представляли опасности взрыва в опасные места. Они были отраслевым стандартом на протяжении многих десятилетий до появления дискретных электронных контроллеров и распределенные системы управления.
Для этих контроллеров был установлен стандарт пневматической промышленной сигнализации 3–15 фунтов на кв. Дюйм (0,2–1,0 бар), который имел повышенный ноль, чтобы гарантировать, что устройства работают в пределах своей линейной характеристики, и представлял собой диапазон регулирования 0–100%.
В 1950-х годах, когда электронные усилители с высоким коэффициентом усиления стали дешевыми и надежными, стали популярны электронные ПИД-регуляторы, и пневматический стандарт был эмулирован 10-50 мА и 4-20 мА. токовая петля сигналы (последний стал отраслевым стандартом). Пневматические приводы поля до сих пор широко используются из-за преимуществ пневматической энергии для регулирующие клапаны в производственных условиях.
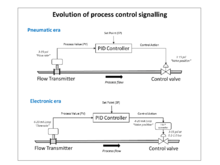
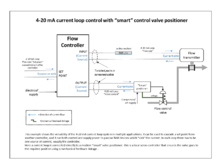
Большинство современных ПИД-регуляторов в промышленности реализованы как компьютерное программное обеспечение в распределенные системы управления (DCS), программируемые логические контроллеры (ПЛК) или дискретные компактные контроллеры.
Электронные аналоговые контроллеры
Электронные аналоговые контуры ПИД-регулирования часто встречаются в более сложных электронных системах, например, при позиционировании головки дисковод, силовое кондиционирование источник питания, или даже схема обнаружения движения современного сейсмометр. Дискретные электронные аналоговые контроллеры были в значительной степени заменены цифровыми контроллерами, использующими микроконтроллеры или же ПЛИС для реализации алгоритмов PID. Тем не менее, дискретные аналоговые ПИД-регуляторы все еще используются в нишевых приложениях, требующих высокой пропускной способности и низкого уровня шума, таких как контроллеры лазерных диодов.[13]
Пример контура управления
Рассмотрим роботизированная рука[14] которые можно перемещать и позиционировать с помощью контура управления. An электрический двигатель может поднимать или опускать руку, в зависимости от приложенной прямой или обратной мощности, но мощность не может быть простой функцией положения из-за инертная масса руки, силы, обусловленные гравитацией, внешние силы на руке, такие как груз, который нужно поднять, или работа, которую необходимо выполнить с внешним объектом.
- Ощущаемая позиция - это переменная процесса (PV).
- Желаемое положение называется уставкой (SP).
- Разница между PV и SP - это ошибка (e), которая количественно определяет, является ли плечо слишком низким или слишком высоким и насколько.
- Вход в процесс ( электрический ток в двигателе) - это выходной сигнал ПИД-регулятора. Она называется либо управляемой переменной (MV), либо управляющей переменной (CV).
Путем измерения положения (PV) и вычитания его из заданного значения (SP) определяется ошибка (e), по которой контроллер вычисляет, какой электрический ток необходимо подать на двигатель (MV).
Пропорциональный
Очевидный метод пропорциональный управление: ток двигателя устанавливается пропорционально имеющейся ошибке. Однако этот метод не работает, если, например, рука должна поднимать другой вес: больший вес требует большей силы, приложенной для той же ошибки на нижней стороне, но меньшей силы, если ошибка находится на верхней стороне. Здесь свою роль играют интегральные и производные члены.
интеграл
An интеграл Срок действия увеличивает действие не только в отношении ошибки, но и времени, в течение которого она сохраняется. Таким образом, если приложенной силы недостаточно, чтобы свести ошибку к нулю, эта сила будет увеличиваться с течением времени. Чистый I-контроллер может свести ошибку к нулю, но он будет как медленным, реагируя вначале (потому что действие будет небольшим вначале, потребуется время, чтобы стать значительным), так и жестким (действие увеличивается, пока ошибка положительный, даже если ошибка начала приближаться к нулю).
Производная
А производная Этот термин учитывает не ошибку (то есть, он не может привести ее к нулю: чистый D-контроллер не может привести систему к ее заданному значению), а скорость изменения ошибки, пытаясь свести эту скорость к нулю. Он направлен на выравнивание траектории ошибки до горизонтальной линии, гашение приложенной силы и, таким образом, уменьшение перерегулирования (ошибка с другой стороны из-за слишком большой приложенной силы). Применение слишком большого импульса при небольшой и уменьшающейся ошибке приведет к перерегулированию. Если после перерегулирования контроллер применит большую коррекцию в противоположном направлении и неоднократно перескакивает желаемое положение, выходной сигнал будет колебаться около заданного значения при постоянном, растущем или убывающем синусоида. Если амплитуда колебаний увеличивается со временем, система нестабильна. Если они уменьшаются, система стабильна. Если колебания остаются на постоянной величине, система незначительно стабильный.
Управление демпфированием
В интересах своевременного и точного достижения контролируемого прибытия в желаемую позицию (SP) управляемая система должна быть критически затухающий. Хорошо настроенная система управления положением также будет подавать необходимые токи на управляемый двигатель, так что рычаг толкает и тянет по мере необходимости, чтобы противостоять внешним силам, пытающимся переместить его из требуемого положения. Само заданное значение может быть создано внешней системой, такой как ПЛК или другой компьютерной системы, поэтому он постоянно меняется в зависимости от работы, которую должен выполнять роботизированный манипулятор. Хорошо настроенная система ПИД-регулирования позволит руке максимально соответствовать этим меняющимся требованиям.
Ответ на беспорядки
Если контроллер запускается из стабильного состояния с нулевой ошибкой (PV = SP), то дальнейшие изменения контроллера будут происходить в ответ на изменения в других измеренных или неизмеренных входных данных процесса, которые влияют на процесс, и, следовательно, на PV. Переменные, которые влияют на процесс, кроме MV, известны как возмущения. Как правило, контроллеры используются для отклонения нарушений и для изменения уставки. Изменение нагрузки на руку представляет собой нарушение процесса управления рукой робота.
Приложения
Теоретически контроллер можно использовать для управления любым процессом, имеющим измеримый выход (PV), известное идеальное значение для этого выхода (SP) и вход процесса (MV), который влияет на соответствующий PV. Контроллеры используются в промышленности для регулирования температура, давление, сила, скорость подачи,[15] скорость потока, химический состав (компонент концентрации ), масса, позиция, скорость, и практически все другие переменные, для которых существует измерение.
Теория регулятора
- В этом разделе описывается параллельная или невзаимодействующая форма ПИД-регулятора. Остальные формы смотрите в разделе Альтернативная номенклатура и формы PID.
Схема управления PID названа в честь трех ее корректирующих членов, сумма которых составляет управляемую переменную (MV). Пропорциональный, интегральный и производный члены суммируются для расчета выходного сигнала ПИД-регулятора. Определение в качестве выхода контроллера окончательная форма алгоритма PID
куда
- - пропорциональное усиление, параметр настройки,
- - интегральный коэффициент усиления, параметр настройки,
- - производное усиление, параметр настройки,
- - ошибка (SP - уставка, а PV (т) - переменная процесса),
- время или мгновенное время (настоящее),
- - переменная интегрирования (принимает значения от времени 0 до настоящего момента ).
Эквивалентно функция передачи в Домен Лапласа ПИД-регулятора
куда - комплексная частота.
Пропорциональный срок

Пропорциональный член дает выходное значение, пропорциональное текущему значению ошибки. Пропорциональный отклик можно отрегулировать, умножив ошибку на постоянную Kп, называемая константой пропорционального усиления.
Пропорциональный член определяется выражением
Высокое пропорциональное усиление приводит к большому изменению выходного сигнала при заданном изменении ошибки. Если пропорциональное усиление слишком велико, система может стать нестабильной (см. раздел о настройке петли ). Напротив, небольшое усиление приводит к небольшому выходному отклику на большую ошибку ввода и к менее отзывчивому или менее чувствительному контроллеру. Если пропорциональное усиление слишком низкое, управляющее воздействие может быть слишком маленьким при реагировании на помехи в системе. Теория настройки и производственная практика указывают на то, что пропорциональный член должен вносить основную часть изменения выпуска.[нужна цитата ]
Постоянная ошибка
В установившаяся ошибка - это разница между желаемым конечным результатом и фактическим.[16] Поскольку для его управления требуется ненулевая ошибка, пропорциональный контроллер обычно работает с установившейся ошибкой.[а] Установившаяся ошибка (SSE) пропорциональна технологическому усилению и обратно пропорциональна пропорциональному усилению. SSE можно уменьшить, добавив компенсирующий термин смещения к заданному значению И выходу или динамически корректируется путем добавления интегрального члена.
Интегральный член
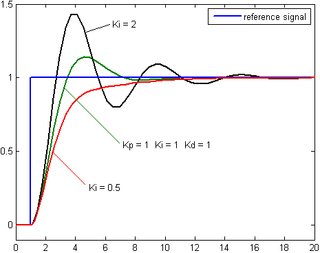
Вклад интегрального члена пропорционален как величине ошибки, так и продолжительности ошибки. В интеграл в ПИД-регуляторе представляет собой сумму мгновенной ошибки во времени и дает накопленное смещение, которое должно было быть скорректировано ранее. Затем накопленная ошибка умножается на интегральный коэффициент усиления (Kя) и добавлен к выходу контроллера.
Интегральный член дается выражением
Интегральный член ускоряет движение процесса к заданному значению и устраняет остаточную установившуюся ошибку, которая возникает при использовании чистого пропорционального регулятора. Однако, поскольку интегральный член является ответом на накопленные ошибки прошлого, он может привести к тому, что текущая стоимость превышение значение уставки (см. раздел о настройке петли ).
Производный термин
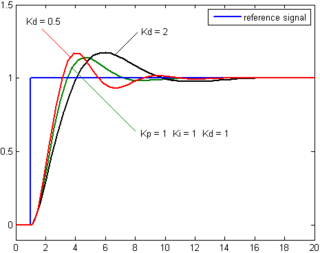
Производная ошибки процесса вычисляется путем определения крутизны ошибки во времени и умножения этой скорости изменения на коэффициент усиления производной. Kd. Величина вклада производного члена в общее управляющее воздействие называется производным усилением, Kd.
Член производной дается формулой
Производное действие предсказывает поведение системы и, таким образом, улучшает время установления и стабильность системы.[17][18] Идеальная производная не причинный, так что реализации ПИД-контроллеров включают дополнительную фильтрацию нижних частот для производной, чтобы ограничить высокочастотное усиление и шум. Однако производное действие на практике используется редко - по одной оценке только в 25% развернутых контроллеров.[нужна цитата ] - из-за его переменного влияния на стабильность системы в реальных приложениях.
Настройка петли
Тюнинг Контур управления - это регулировка его параметров управления (диапазон пропорциональности / усиление, интегральное усиление / сброс, производное усиление / скорость) до оптимальных значений для желаемой реакции управления. Стабильность (отсутствие неограниченных колебаний) является основным требованием, но помимо этого, разные системы имеют разное поведение, разные приложения имеют разные требования, и требования могут конфликтовать друг с другом.
Настройка ПИД-регулятора - сложная проблема, несмотря на то, что существует всего три параметра и в принципе ее просто описать, поскольку она должна удовлетворять сложным критериям в пределах ограничения ПИД-регулирования. Соответственно, существуют различные методы настройки контура, и более сложные методы являются предметом патентов; В этом разделе описаны некоторые традиционные ручные методы настройки контура.
Проектирование и настройка ПИД-регулятора кажутся концептуально интуитивно понятными, но могут быть трудными на практике, если необходимо достичь нескольких (и часто противоречащих друг другу) целей, таких как короткие переходные процессы и высокая стабильность. ПИД-регуляторы часто обеспечивают приемлемое управление с использованием настроек по умолчанию, но производительность обычно может быть улучшена путем тщательной настройки, а производительность может быть неприемлемой при плохой настройке. Обычно первоначальные конструкции необходимо многократно корректировать посредством компьютерного моделирования, пока система с обратной связью не сработает или не откажется от желаемого.
Некоторые процессы имеют степень нелинейность и поэтому параметры, которые хорошо работают в условиях полной нагрузки, не работают, когда процесс запускается без нагрузки; это можно исправить планирование усиления (с разными параметрами в разных регионах).
Стабильность
Если параметры ПИД-регулятора (коэффициенты усиления пропорционального, интегрального и производного членов) выбраны неправильно, вход управляемого процесса может быть нестабильным, т.е. его выход расходится, с или без колебание, и ограничивается только насыщением или механическим разрушением. Нестабильность вызвана избыток усиление, особенно при наличии значительного лага.
Как правило, требуется стабилизация реакции, и процесс не должен колебаться при любой комбинации условий процесса и уставок, хотя иногда предельная стабильность (ограниченное колебание) приемлемо или желательно.[нужна цитата ]
Математически истоки нестабильности можно увидеть в Домен Лапласа.[19]
Полная передаточная функция контура:
куда
- - передаточная функция ПИД-регулятора и
- передаточная функция растения
Система называется нестабильной, если передаточная функция замкнутого контура расходится при некоторых .[19] Это происходит в ситуациях, когда . Обычно это происходит, когда с фазовым сдвигом 180 градусов. Стабильность гарантирована, когда для частот с большим фазовым сдвигом. Более общий формализм этого эффекта известен как Критерий устойчивости Найквиста.
Оптимальное поведение
Оптимальное поведение при изменении процесса или изменении уставки зависит от приложения.
Два основных требования: регулирование (подавление помех - сохранение заданного значения) и отслеживание команд (реализация изменений уставки) - они относятся к тому, насколько хорошо регулируемая переменная отслеживает желаемое значение. Конкретные критерии для отслеживания команд включают: время нарастания и время установления. Некоторые процессы не должны допускать превышения переменной процесса за пределы уставки, если, например, это было бы небезопасно. Другие процессы должны минимизировать энергию, затрачиваемую на достижение новой уставки.
Обзор методов настройки
Существует несколько методов настройки контура ПИД-регулирования. Наиболее эффективные методы обычно включают разработку какой-либо модели процесса с последующим выбором P, I и D на основе параметров динамической модели. Методы ручной настройки могут занять относительно много времени, особенно для систем с большим временем цикла.
Выбор метода будет во многом зависеть от того, можно ли отключить цикл для настройки, а также от времени отклика системы. Если систему можно перевести в автономный режим, лучший метод настройки часто включает в себя пошаговое изменение входных данных, измерение выхода как функции времени и использование этого отклика для определения параметров управления.[нужна цитата ]
| Метод | Преимущества | Недостатки |
|---|---|---|
| Ручная настройка | Математика не требуется; онлайн. | Требуется опытный персонал.[нужна цитата ] |
| Зиглер-Николс [b] | Проверенный метод; онлайн. | Расстройство процесса, несколько проб и ошибок, очень агрессивная настройка.[нужна цитата ] |
| Тайреус Люибен | Проверенный метод; онлайн. | Расстройство процесса, несколько проб и ошибок, очень агрессивная настройка.[нужна цитата ] |
| Программные инструменты | Последовательный тюнинг; онлайн или офлайн - может использовать компьютерно-автоматизированную систему управления (CAutoD ) техники; может включать анализ клапана и датчика; позволяет моделировать перед загрузкой; может поддерживать нестационарную настройку (NSS). | Требуются некоторые затраты или обучение.[21] |
| Коэн-Кун | Хорошие модели процессов. | Немного математики; не в сети; подходит только для процессов первого порядка.[нужна цитата ] |
| Остром-Хэгглунд | Может использоваться для автонастройки; амплитуда минимальна, поэтому этот метод имеет наименьшее нарушение технологического процесса | Сам процесс по своей природе является колебательным.[нужна цитата ] |
Ручная настройка
Если система должна оставаться в сети, один из методов настройки - сначала установить и значения к нулю. Увеличить пока выход петли не будет колебаться, тогда должен быть установлен примерно на половину этого значения для ответа типа «затухание четверти амплитуды». Затем увеличивайте до тех пор, пока любое смещение не будет исправлено за достаточное время для процесса. Однако слишком много вызовет нестабильность. Наконец, увеличьте , если требуется, до тех пор, пока контур не станет достаточно быстро для достижения своей ссылки после нарушения нагрузки. Однако слишком много вызовет чрезмерную реакцию и перерегулирование. При быстрой настройке контура ПИД-регулятора обычно наблюдается небольшой перерегулирование, чтобы быстрее достичь уставки; однако некоторые системы не могут принять перерегулирование, и в этом случае чрезмерно демпфированный требуется замкнутая система, которая потребует установка значительно меньше, чем половина настройка, вызывающая колебания.[нужна цитата ]
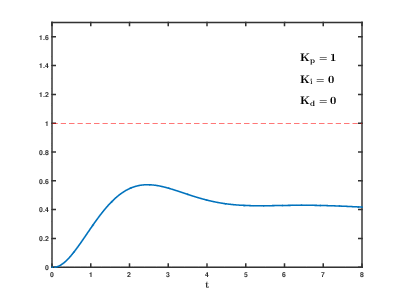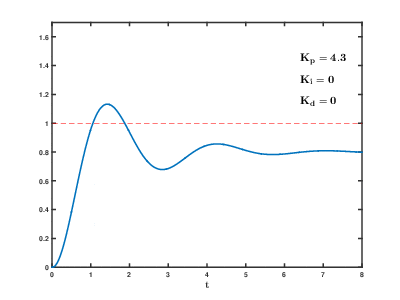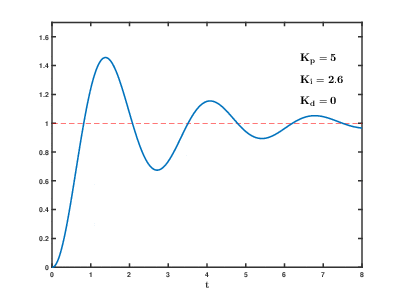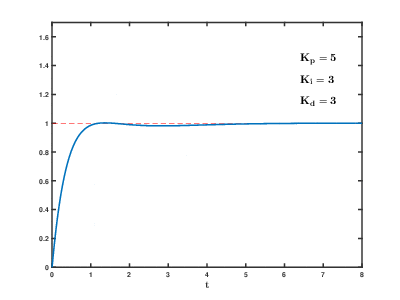
| Параметр | Время нарастания | Перескок | Время установления | Постоянная ошибка | Стабильность |
|---|---|---|---|---|---|
| Снижаться | Увеличивать | Небольшой изменение | Снижаться | Деградировать | |
| Снижаться | Увеличивать | Увеличивать | Устранять | Деградировать | |
| Незначительное изменение | Снижаться | Снижаться | Теоретически нет эффекта | Улучшение, если маленький |
Метод Циглера – Николса
Другой метод эвристической настройки известен как Метод Циглера – Николса, представлен Джон Г. Зиглер и Натаниэль Б. Николс в 1940-е гг. Как и в методе выше, и сначала устанавливаются нулевые коэффициенты усиления. Пропорциональное усиление увеличивается, пока не будет достигнуто окончательное усиление, , при котором выход контура начинает постоянно колебаться. и период колебаний используются для установки следующих коэффициентов усиления:
| Тип управления | |||
|---|---|---|---|
| п | — | — | |
| ЧИСЛО ПИ | — | ||
| PID |
Эти преимущества применимы к идеальной параллельной форме ПИД-регулятора. Применительно к стандартной форме ПИД-регулятора только интегральный и производный коэффициенты усиления и зависят от периода колебаний .
Параметры Коэна – Куна
Этот метод был разработан в 1953 году и основан на модели первого порядка + временная задержка. Подобно Метод Циглера – Николса был разработан набор параметров настройки для получения отклика с обратной связью с коэффициентом затухания 1/4. Возможно, самая большая проблема с этими параметрами заключается в том, что небольшое изменение параметров процесса потенциально может привести к нестабильности замкнутой системы.
Релейный (Åström – Hägglund) метод
Опубликовано в 1984 г. Карл Йохан Остром и Торе Хэгглунд,[24] the relay method temporarily operates the process using взрывной контроль and measures the resultant oscillations. The output is switched (as if by a реле, hence the name) between two values of the control variable. The values must be chosen so the process will cross the setpoint, but need not be 0% and 100%; by choosing suitable values, dangerous oscillations can be avoided.
As long as the process variable is below the setpoint, the control output is set to the higher value. As soon as it rises above the setpoint, the control output is set to the lower value. Ideally, the output waveform is nearly square, spending equal time above and below the setpoint. The period and amplitude of the resultant oscillations are measured, and used to compute the ultimate gain and period, which are then fed into the Ziegler–Nichols method.
Specifically, the ultimate period is assumed to be equal to the observed period, and the ultimate gain is computed as куда а is the amplitude of the process variable oscillation, and б is the amplitude of the control output change which caused it.
There are numerous variants on the relay method.[25]
First with dead time model
The transfer function for a first-order process, with dead time, is:
where kп is the process gain, τп is the time constant, θ is the dead time, and u(s) is a step change input. Converting this transfer function to the time domain results in:
using the same parameters found above.
It is important when using this method to apply a large enough step change input that the output can be measured; however, too large of a step change can affect the process stability. Additionally, a larger step change will ensure that the output is not changing due to a disturbance (for best results, try to minimize disturbances when performing the step test).
One way to determine the parameters for the first-order process is using the 63.2% method. In this method, the process gain (kп) is equal to the change in output divided by the change in input. The dead time (θ) is the amount of time between when the step change occurred and when the output first changed. The time constant (τп) is the amount of time it takes for the output to reach 63.2% of the new steady-state value after the step change. One downside to using this method is that the time to reach a new steady-state value can take a while if the process has a large time constants. [26]
Tuning software
Most modern industrial facilities no longer tune loops using the manual calculation methods shown above. Instead, PID tuning and loop optimization software are used to ensure consistent results. These software packages will gather the data, develop process models, and suggest optimal tuning. Some software packages can even develop tuning by gathering data from reference changes.
Mathematical PID loop tuning induces an impulse in the system, and then uses the controlled system's frequency response to design the PID loop values. In loops with response times of several minutes, mathematical loop tuning is recommended, because trial and error can take days just to find a stable set of loop values. Optimal values are harder to find. Some digital loop controllers offer a self-tuning feature in which very small setpoint changes are sent to the process, allowing the controller itself to calculate optimal tuning values.
Another approach calculates initial values via the Ziegler–Nichols method, and uses a numerical optimization technique to find better PID coefficients.[27]
Other formulas are available to tune the loop according to different performance criteria. Many patented formulas are now embedded within PID tuning software and hardware modules.[28]
Advances in automated PID loop tuning software also deliver algorithms for tuning PID Loops in a dynamic or non-steady state (NSS) scenario. The software will model the dynamics of a process, through a disturbance, and calculate PID control parameters in response.[29]
Ограничения
While PID controllers are applicable to many control problems, and often perform satisfactorily without any improvements or only coarse tuning, they can perform poorly in some applications, and do not in general provide оптимальный control. The fundamental difficulty with PID control is that it is a feedback control system, with постоянный parameters, and no direct knowledge of the process, and thus overall performance is reactive and a compromise. While PID control is the best controller in an наблюдатель without a model of the process, better performance can be obtained by overtly modeling the actor of the process without resorting to an observer.
PID controllers, when used alone, can give poor performance when the PID loop gains must be reduced so that the control system does not overshoot, oscillate or охота about the control setpoint value. They also have difficulties in the presence of non-linearities, may trade-off regulation versus response time, do not react to changing process behavior (say, the process changes after it has warmed up), and have lag in responding to large disturbances.
The most significant improvement is to incorporate feed-forward control with knowledge about the system, and using the PID only to control error. Alternatively, PIDs can be modified in more minor ways, such as by changing the parameters (either gain scheduling in different use cases or adaptively modifying them based on performance), improving measurement (higher sampling rate, precision, and accuracy, and low-pass filtering if necessary), or cascading multiple PID controllers.
Линейность
Another problem faced with PID controllers is that they are linear, and in particular symmetric. Thus, performance of PID controllers in non-linear systems (such as Системы HVAC ) is variable. For example, in temperature control, a common use case is active heating (via a heating element) but passive cooling (heating off, but no cooling), so overshoot can only be corrected slowly – it cannot be forced downward. In this case the PID should be tuned to be overdamped, to prevent or reduce overshoot, though this reduces performance (it increases settling time).
Noise in derivative
A problem with the derivative term is that it amplifies higher frequency measurement or process шум that can cause large amounts of change in the output. It is often helpful to filter the measurements with a фильтр нижних частот in order to remove higher-frequency noise components. As low-pass filtering and derivative control can cancel each other out, the amount of filtering is limited. Therefore, low noise instrumentation can be important. A nonlinear median filter may be used, which improves the filtering efficiency and practical performance.[30] In some cases, the differential band can be turned off with little loss of control. This is equivalent to using the PID controller as a ПИ-регулятор.
Modifications to the algorithm
The basic PID algorithm presents some challenges in control applications that have been addressed by minor modifications to the PID form.
Integral windup
One common problem resulting from the ideal PID implementations is integral windup. Following a large change in setpoint the integral term can accumulate an error larger than the maximal value for the regulation variable (windup), thus the system overshoots and continues to increase until this accumulated error is unwound. This problem can be addressed by:
- Disabling the integration until the PV has entered the controllable region
- Preventing the integral term from accumulating above or below pre-determined bounds
- Back-calculating the integral term to constrain the regulator output within feasible bounds.[31]
Overshooting from known disturbances
For example, a PID loop is used to control the temperature of an electric resistance furnace where the system has stabilized. Now when the door is opened and something cold is put into the furnace the temperature drops below the setpoint. The integral function of the controller tends to compensate for error by introducing another error in the positive direction. This overshoot can be avoided by freezing of the integral function after the opening of the door for the time the control loop typically needs to reheat the furnace.
ПИ-регулятор

А ПИ-регулятор (proportional-integral controller) is a special case of the PID controller in which the derivative (D) of the error is not used.
The controller output is given by
куда is the error or deviation of actual measured value (PV) from the setpoint (SP).
A PI controller can be modelled easily in software such as Simulink или же Xcos using a "flow chart" box involving Лаплас операторы:
куда
- = proportional gain
- = integral gain
Setting a value for is often a trade off between decreasing overshoot and increasing settling time.
The lack of derivative action may make the system more steady in the steady state in the case of noisy data. This is because derivative action is more sensitive to higher-frequency terms in the inputs.
Without derivative action, a PI-controlled system is less responsive to real (non-noise) and relatively fast alterations in state and so the system will be slower to reach setpoint and slower to respond to perturbations than a well-tuned PID system may be.
Зона нечувствительности
Many PID loops control a mechanical device (for example, a valve). Mechanical maintenance can be a major cost and wear leads to control degradation in the form of either прикол или же люфт in the mechanical response to an input signal. The rate of mechanical wear is mainly a function of how often a device is activated to make a change. Where wear is a significant concern, the PID loop may have an output deadband to reduce the frequency of activation of the output (valve). This is accomplished by modifying the controller to hold its output steady if the change would be small (within the defined deadband range). The calculated output must leave the deadband before the actual output will change.
Setpoint step change
The proportional and derivative terms can produce excessive movement in the output when a system is subjected to an instantaneous step increase in the error, such as a large setpoint change. In the case of the derivative term, this is due to taking the derivative of the error, which is very large in the case of an instantaneous step change. As a result, some PID algorithms incorporate some of the following modifications:
- Setpoint ramping
- In this modification, the setpoint is gradually moved from its old value to a newly specified value using a linear or first order differential ramp function. Это позволяет избежать прерывность present in a simple step change.
- Derivative of the process variable
- In this case the PID controller measures the derivative of the measured переменная процесса (PV), rather than the derivative of the error. This quantity is always continuous (i.e., never has a step change as a result of changed setpoint). This modification is a simple case of setpoint weighting.
- Setpoint weighting
- Setpoint weighting adds adjustable factors (usually between 0 and 1) to the setpoint in the error in the proportional and derivative element of the controller. The error in the integral term must be the true control error to avoid steady-state control errors. These two extra parameters do not affect the response to load disturbances and measurement noise and can be tuned to improve the controller's setpoint response.
Прямая связь
The control system performance can be improved by combining the Обратная связь (or closed-loop) control of a PID controller with feed-forward (or open-loop) control. Knowledge about the system (such as the desired acceleration and inertia) can be fed forward and combined with the PID output to improve the overall system performance. The feed-forward value alone can often provide the major portion of the controller output. The PID controller primarily has to compensate whatever difference or ошибка remains between the setpoint (SP) and the system response to the open-loop control. Since the feed-forward output is not affected by the process feedback, it can never cause the control system to oscillate, thus improving the system response without affecting stability. Feed forward can be based on the setpoint and on extra measured disturbances. Setpoint weighting is a simple form of feed forward.
For example, in most motion control systems, in order to accelerate a mechanical load under control, more force is required from the actuator. If a velocity loop PID controller is being used to control the speed of the load and command the force being applied by the actuator, then it is beneficial to take the desired instantaneous acceleration, scale that value appropriately and add it to the output of the PID velocity loop controller. This means that whenever the load is being accelerated or decelerated, a proportional amount of force is commanded from the actuator regardless of the feedback value. The PID loop in this situation uses the feedback information to change the combined output to reduce the remaining difference between the process setpoint and the feedback value. Working together, the combined open-loop feed-forward controller and closed-loop PID controller can provide a more responsive control system.
Bumpless operation
PID controllers are often implemented with a "bumpless" initialization feature that recalculates the integral accumulator term to maintain a consistent process output through parameter changes.[32] A partial implementation is to store the integral gain times the error rather than storing the error and postmultiplying by the integral gain, which prevents discontinuous output when the I gain is changed, but not the P or D gains.
Прочие улучшения
In addition to feed-forward, PID controllers are often enhanced through methods such as PID gain scheduling (changing parameters in different operating conditions), нечеткая логика, или же вычислительная глагольная логика.[33][34] Further practical application issues can arise from instrumentation connected to the controller. A high enough sampling rate, measurement precision, and measurement accuracy are required to achieve adequate control performance. Another new method for improvement of PID controller is to increase the degree of freedom by using fractional order. The order of the integrator and differentiator add increased flexibility to the controller.[35]
Cascade control
One distinctive advantage of PID controllers is that two PID controllers can be used together to yield better dynamic performance. This is called cascaded PID control. Two controllers are in cascade when they are arranged so that one regulates the set point of the other. A PID controller acts as outer loop controller, which controls the primary physical parameter, such as fluid level or velocity. The other controller acts as inner loop controller, which reads the output of outer loop controller as setpoint, usually controlling a more rapid changing parameter, flowrate or acceleration. It can be mathematically proven[нужна цитата ] that the working frequency of the controller is increased and the time constant of the object is reduced by using cascaded PID controllers.[нечеткий ].
For example, a temperature-controlled circulating bath has two PID controllers in cascade, each with its own thermocouple temperature sensor. The outer controller controls the temperature of the water using a thermocouple located far from the heater, where it accurately reads the temperature of the bulk of the water. The error term of this PID controller is the difference between the desired bath temperature and measured temperature. Instead of controlling the heater directly, the outer PID controller sets a heater temperature goal for the inner PID controller. The inner PID controller controls the temperature of the heater using a thermocouple attached to the heater. The inner controller's error term is the difference between this heater temperature setpoint and the measured temperature of the heater. Its output controls the actual heater to stay near this setpoint.
The proportional, integral, and differential terms of the two controllers will be very different. The outer PID controller has a long time constant – all the water in the tank needs to heat up or cool down. The inner loop responds much more quickly. Each controller can be tuned to match the physics of the system Это controls – heat transfer and thermal mass of the whole tank or of just the heater – giving better total response.
Alternative nomenclature and forms
Standard versus parallel (ideal) form
The form of the PID controller most often encountered in industry, and the one most relevant to tuning algorithms is the стандартная форма. In this form the gain is applied to the , и terms, yielding:
куда
- это интегральное время
- это производное время
In this standard form, the parameters have a clear physical meaning. In particular, the inner summation produces a new single error value which is compensated for future and past errors. The proportional error term is the current error. The derivative components term attempts to predict the error value at seconds (or samples) in the future, assuming that the loop control remains unchanged. The integral component adjusts the error value to compensate for the sum of all past errors, with the intention of completely eliminating them in seconds (or samples). The resulting compensated single error value is then scaled by the single gain to compute the control variable.
In the parallel form, shown in the controller theory section
the gain parameters are related to the parameters of the standard form through и . This parallel form, where the parameters are treated as simple gains, is the most general and flexible form. However, it is also the form where the parameters have the least physical interpretation and is generally reserved for theoretical treatment of the PID controller. The standard form, despite being slightly more complex mathematically, is more common in industry.
Reciprocal gain, a.k.a. proportional band
In many cases, the manipulated variable output by the PID controller is a dimensionless fraction between 0 and 100% of some maximum possible value, and the translation into real units (such as pumping rate or watts of heater power) is outside the PID controller. The process variable, however, is in dimensioned units such as temperature. It is common in this case to express the gain not as "output per degree", but rather in the reciprocal form of a полоса пропорциональности , which is "degrees per full output": the range over which the output changes from 0 to 1 (0% to 100%). Beyond this range, the output is saturated, full-off or full-on. The narrower this band, the higher the proportional gain.
Basing derivative action on PV
In most commercial control systems, derivative action is based on process variable rather than error. That is, a change in the setpoint does not affect the derivative action. This is because the digitized version of the algorithm produces a large unwanted spike when the setpoint is changed. If the setpoint is constant then changes in the PV will be the same as changes in error. Therefore, this modification makes no difference to the way the controller responds to process disturbances.
Basing proportional action on PV
Most commercial control systems offer the вариант of also basing the proportional action solely on the process variable. This means that only the integral action responds to changes in the setpoint. The modification to the algorithm does not affect the way the controller responds to process disturbances.Basing proportional action on PV eliminates the instant and possibly very large change in output caused by a sudden change to the setpoint. Depending on the process and tuning this may be beneficial to the response to a setpoint step.
король[36] describes an effective chart-based method.
Laplace form
Sometimes it is useful to write the PID regulator in Преобразование Лапласа форма:
Having the PID controller written in Laplace form and having the transfer function of the controlled system makes it easy to determine the closed-loop transfer function of the system.
Series/interacting form
Another representation of the PID controller is the series, or interacting форма
where the parameters are related to the parameters of the standard form through
- , , и
с
- .
This form essentially consists of a PD and PI controller in series, and it made early (analog) controllers easier to build. When the controllers later became digital, many kept using the interacting form.
Discrete implementation
The analysis for designing a digital implementation of a PID controller in a микроконтроллер (MCU) или FPGA device requires the standard form of the PID controller to be дискретизированный.[37] Approximations for first-order derivatives are made by backward конечные разности. The integral term is discretized, with a sampling time , as follows,
The derivative term is approximated as,
Таким образом, velocity algorithm for implementation of the discretized PID controller in a MCU is obtained by differentiating , using the numerical definitions of the first and second derivative and solving for and finally obtaining:
s.t.
Псевдокод
Here is a simple software loop that implements a PID algorithm:[38]
previous_error := 0integral := 0loop: error := setpoint − measured_value integral := integral + error × dt derivative := (error − previous_error) / dt output := Kp × error + Ki × integral + Kd × derivative previous_error := error wait(dt) goto loop
In this example, two variables that will be maintained within the loop are инициализирован to zero, then the loop begins. Электрический ток ошибка is calculated by subtracting the measured_value (the process variable, or PV) from the current уставка (SP). Потом, интеграл и производная values are calculated, and these and the ошибка are combined with three preset gain terms – the proportional gain, the integral gain and the derivative gain – to derive an выход ценить.
In the real world, this is D-to-A converted and passed into the process under control as the manipulated variable (MV). The current error is stored elsewhere for re-use in the next differentiation, the program then waits until dt seconds have passed since start, and the loop begins again, reading in new values for the PV and the setpoint and calculating a new value for the error.[38]
Note that for real code, the use of "wait(dt)" might be inappropriate because it doesn't account for time taken by the algorithm itself during the loop, or more importantly, any preemption delaying the algorithm.
Смотрите также
Примечания
- ^ The only exception is where the target value is the same as the value obtained when the controller output is zero.
- ^ A common assumption often made for Proportional-Integral-Derivative (PID) control design, as done by Ziegler and Nichols, is to take the integral time constant to be four times the derivative time constant. Although this choice is reasonable, selecting the integral time constant to have this value may have had something to do with the fact that, for the ideal case with a derivative term with no filter, the PID transfer function consists of two real and equal zeros in the numerator.[20]
Рекомендации
- ^ Araki, M. "PID Control" (PDF).
- ^ Hills, Richard L (1996), Сила ветра, Издательство Кембриджского университета
- ^ Richard E. Bellman (December 8, 2015). Adaptive Control Processes: A Guided Tour. Издательство Принстонского университета. ISBN 9781400874668.
- ^ а б c d е ж Bennett, Stuart (1996). "A brief history of automatic control" (PDF). Журнал IEEE Control Systems. 16 (3): 17–25. Дои:10.1109/37.506394. Архивировано из оригинал (PDF) on 2016-08-09. Получено 2014-08-21.
- ^ Maxwell, J. C. (1868). «О губернаторах» (PDF). Труды Королевского общества. 100.
- ^ Newpower, Anthony (2006). Iron Men and Tin Fish: The Race to Build a Better Torpedo during World War II. Praeger Security International. ISBN 978-0-275-99032-9. п. цитируя Gray, Edwyn (1991), The Devil's Device: Robert Whitehead and the History of the Torpedo, Annapolis, MD: U.S. Naval Institute, p. 33.
- ^ Sleeman, C. W. (1880), Torpedoes and Torpedo Warfare, Portsmouth: Griffin & Co., pp. 137–138,
which constitutes what is termed as the secret of the fish torpedo.
- ^ "A Brief Building Automation History". Архивировано из оригинал на 2011-07-08. Получено 2011-04-04.
- ^ Минорский, Николай (1922). «Курсовая устойчивость автоматически управляемых кузовов». J. Amer. Soc. Naval Eng. 34 (2): 280–309. Дои:10.1111 / j.1559-3584.1922.tb04958.x.
- ^ Bennett 1993, п. 67
- ^ Bennett, Stuart (June 1986). A history of control engineering, 1800-1930. ИЭПП. стр.142–148. ISBN 978-0-86341-047-5.
- ^ Shinskey, F Greg (2004), The power of external-reset feedback (PDF), Control Global
- ^ Neuhaus, Rudolf. "Diode Laser Locking and Linewidth Narrowing" (PDF). Получено 8 июня, 2015.
- ^ "Position control system" (PDF). Hacettepe University Department of Electrical and Electronics Engineering.
- ^ Kebriaei, Reza; Frischkorn, Jan; Reese, Stefanie; Husmann, Tobias; Meier, Horst; Moll, Heiko; Theisen, Werner (2013). "Numerical modelling of powder metallurgical coatings on ring-shaped parts integrated with ring rolling". Material Processing Technology. 213 (1): 2015–2032. Дои:10.1016/j.jmatprotec.2013.05.023.
- ^ Lipták, Béla G. (2003). Instrument Engineers' Handbook: Process control and optimization (4-е изд.). CRC Press. п. 108. ISBN 0-8493-1081-4.
- ^ "Introduction: PID Controller Design". Университет Мичигана.
- ^ Tim Wescott (October 2000). "PID without a PhD" (PDF). EE Times-India. Цитировать журнал требует
| журнал =(помощь) - ^ а б Бечхофер, Джон (2005). «Обратная связь для физиков: учебное эссе по управлению». Обзоры современной физики. 77 (3): 783–835. Bibcode:2005РвМП ... 77..783Б. CiteSeerX 10.1.1.124.7043. Дои:10.1103 / revmodphys.77.783.
- ^ Atherton, Drek P (December 2014). "Almost Six Decades in Control Engineering". Журнал IEEE Control Systems. 34 (6): 103–110. Дои:10.1109/MCS.2014.2359588. S2CID 20233207.
- ^ Li, Y., et al. (2004) CAutoCSD - Evolutionary search and optimisation enabled computer automated control system design, Int J Automation and Computing, vol. 1, No. 1, pp. 76-88. ISSN 1751-8520.
- ^ Kiam Heong Ang; Чонг, G .; Yun Li (2005). "PID control system analysis, design, and technology" (PDF). IEEE Transactions по технологии систем управления. 13 (4): 559–576. Дои:10.1109/TCST.2005.847331. S2CID 921620.
- ^ Jinghua Zhong (Spring 2006). "PID Controller Tuning: A Short Tutorial" (PDF). Архивировано из оригинал (PDF) на 2015-04-21. Получено 2011-04-04. Цитировать журнал требует
| журнал =(помощь) - ^ Åström, K.J.; Hägglund, T. (July 1984). "Automatic Tuning of Simple Regulators". Объемы разбирательств МФБ. 17 (2): 1867–1872. Дои:10.1016/S1474-6670(17)61248-5.
- ^ Hornsey, Stephen (29 October 2012). "A Review of Relay Auto-tuning Methods for the Tuning of PID-type Controllers". Новое изобретение. 5 (2).
- ^ Bequette, B. Wayne (2003). Управление процессами: моделирование, проектирование и симуляция. Upper Saddle River, New Jersey: Prentice Hall. п. 129. ISBN 978-0-13-353640-9.
- ^ Хейнянен, Ээро (октябрь 2018 г.). Метод автоматической настройки ПИД-регулятора после оптимизации Лууса-Яаколы (PDF) (Магистерская диссертация под ред.). Тампере, Финляндия: Технологический университет Тампере. Получено 1 февраля, 2019.
- ^ Ли, Юнь; Анг, Киам Хеонг; Чонг, Грегори С.Й. (Февраль 2006 г.). «Патенты, программное обеспечение и оборудование для ПИД-регулирования: обзор и анализ современного уровня техники» (PDF). Журнал IEEE Control Systems. 26 (1): 42–54. Дои:10.1109 / MCS.2006.1580153. S2CID 18461921.
- ^ Солтес, Кристиан (январь 2012 г.). Об автоматизации процедуры настройки ПИД-регулятора (PDF) (Лиценциат это). Лундский университет. 847ca38e-93e8-4188-b3d5-8ec6c23f2132.
- ^ Ли, Ю. и Анг, К.Х. и Чонг, G.C.Y. (2006) Анализ и проектирование системы ПИД-регулирования - Проблемы, решения и будущие направления. Журнал IEEE Control Systems, 26 (1). С. 32-41. ISSN 0272-1708
- ^ Купер, Дуглас. «Интегральное (сброс) закручивание, логика оболочки и форма PI Velocity». Получено 2014-02-18.
- ^ Купер, Дуглас. «ПИ-регулирование теплообменника». Практическое управление процессом от Control Guru. Получено 2014-02-27.
- ^ Ян Т. (июнь 2005 г.). «Архитектуры вычислительных контроллеров глагола: к новой парадигме интеллектуального управления». Международный журнал вычислительного познания. 3 (2): 74–101. CiteSeerX 10.1.1.152.9564.
- ^ Лян, Илун; Ян, Дао (2009). «Управление устройством отжига топлива с помощью вычислительных глагольных ПИД-регуляторов». Материалы 3-й Международной конференции по борьбе с контрафакцией, безопасности и идентификации в коммуникации: 417–420.
- ^ Tenreiro Machado JA и др. (2009). «Некоторые приложения дробного исчисления в технике». Математические проблемы в инженерии. 2010: 1–34. Дои:10.1155/2010/639801. HDL:10400.22/4306.
- ^ Король, Майк (2011). Управление процессами: практический подход. Вайли. С. 52–78. ISBN 978-0-470-97587-9.
- ^ «Разработка и анализ дискретных ПИ и ПИД-регуляторов для цифровой реализации». Scribd.com. Получено 2011-04-04.
- ^ а б «ПИД-регулирование процесса, пример« Круиз-контроля »». CodeProject. 2009 г.. Получено 4 ноября 2012.
- Бекетт, Б. Уэйн (2006). Управление процессами: моделирование, проектирование и симуляция. Prentice Hall PTR. ISBN 9789861544779.
дальнейшее чтение
- Липтак, Бела (1995). Справочник инженеров по КИП: управление процессом. Рэднор, Пенсильвания: Книжная компания Чилтона. С. 20–29. ISBN 978-0-8019-8242-2.
- Тан, Кок Кионг; Ван Цин-Го; Ханг Чанг Чи (1999). Достижения в ПИД-регулировании. Лондон, Великобритания: Springer-Verlag. ISBN 978-1-85233-138-2.
- Король, Майк (2010). Управление процессами: практический подход. Чичестер, Великобритания: John Wiley & Sons Ltd. ISBN 978-0-470-97587-9.
- Ван Дорен, Вэнс Дж. (1 июля 2003 г.). "Основы настройки петли". Техника управления.
- Продавцы, Дэвид. «Обзор пропорционального, интегрального и производного управления и предложения по его успешному применению и внедрению» (PDF). Архивировано из оригинал (PDF) 7 марта 2007 г.. Получено 2007-05-05.
- Грэм, Рон; Майк МакХью (2005-10-03). «FAQ по настройке ПИД-регулятора». Майк Макхью. Архивировано из оригинал 6 февраля 2005 г.. Получено 2009-01-05.
- Эйдан О'Дуайер (2009). Справочник правил настройки ПИ- и ПИД-регуляторов (PDF) (3-е изд.). Imperial College Press. ISBN 978-1-84816-242-6.
внешняя ссылка
- Настройка ПИД-регулятора с помощью Mathematica
- Настройка PID с использованием Python
- Принципы ПИД-регулирования и настройки
- Введение в ключевые термины, связанные с ПИД-регулированием температуры
Учебники по PID
- ПИД-регулирование в MATLAB / Simulink и Python с TCLab
- Во всяком случае, что это все за P-I-D? Статья в электронном дизайне
- Показывает, как построить ПИД-регулятор с основными электронными компонентами. (стр.22)
- ПИД без докторской степени
- ПИД-регулирование с помощью MATLAB и Simulink
- ПИД-регулятор с одним операционным усилителем
- Проверенные методы и передовая практика для ПИД-регулирования
- Принципы ПИД-регулирования и настройки
- Руководство по настройке ПИД-регулятора: передовой подход к пониманию и настройке ПИД-регуляторов
- Майкл Барр (30 июля 2002 г.), Введение в управление с обратной связью, Программирование встраиваемых систем, заархивировано оригинал на 2010-02-09
- Цзинхуа Чжун, Машиностроение, Университет Пердью (весна 2006 г.). «Настройка ПИД-регулятора: краткое руководство» (PDF). Архивировано из оригинал (PDF) на 2015-04-21. Получено 2013-12-04.CS1 maint: несколько имен: список авторов (связь)
- Введение в контроллер P, PI, PD и PID с MATLAB







































































![{ displaystyle u (t_ {k}) = u (t_ {k-1}) + K_ {p} left [ left (1 + { dfrac { Delta t} {T_ {i}}} + { dfrac {T_ {d}} { Delta t}} right) e (t_ {k}) + left (-1 - { dfrac {2T_ {d}} { Delta t}} right) e (t_ {k-1}) + { dfrac {T_ {d}} { Delta t}} e (t_ {k-2}) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e71fa41e1c58fcef6f2a3a4118577458ce29c659)
