Таблица перехода состояний - State-transition table
В теория автоматов и последовательная логика, а таблица переходов между состояниями таблица, показывающая, в каком состоянии (или состояниях в случае недетерминированный конечный автомат ) а конечный автомат перейдет в зависимости от текущего состояния и других входных данных. По сути, это таблица истинности в котором входы включают текущее состояние вместе с другими входами, а выходы включают следующее состояние вместе с другими выходами.
Таблица переходов состояний - один из многих способов указать конечный автомат. Другие способы включают диаграмма состояний.
Общие формы
Одномерный
Таблицы перехода состояний иногда представляют собой одномерные таблицы, также называемые таблицы характеристик. Они больше похожи на таблицы истинности, чем на их двумерную форму. Одно измерение указывает входы, текущие состояния, следующие состояния и (необязательно) выходы, связанные с переходами между состояниями.
| Вход | Текущее состояние | Следующее состояние | Выход |
|---|---|---|---|
| я1 | S1 | Sя | ОИкс |
| я2 | S1 | Sj | Оу |
| … | … | … | … |
| яп | S1 | Sk | Оz |
| я1 | S2 | Sя' | ОИкс' |
| я2 | S2 | Sj ′ | Оy ′ |
| … | … | … | … |
| яп | S2 | Sk ′ | Оz ′ |
| … | … | … | … |
| я1 | Sм | Sя" | ОИкс" |
| я2 | Sм | Sj ″ | Оу ″ |
| … | … | … | … |
| яп | Sм | Sk ″ | Оz ″ |
Двухмерный
Таблицы переходов между состояниями обычно представляют собой двумерные таблицы. Есть два распространенных способа их размещения.
В первом случае одно из измерений указывает текущее состояние, а другое - входные данные. Пересечения строк / столбцов указывают следующие состояния и (необязательно) выходы, связанные с переходами состояний.
Вход Текущее состояние | я1 | я2 | … | яп |
|---|---|---|---|---|
| S1 | Sя/ OИкс | Sj/ Oу | … | Sk/ Oz |
| S2 | Sя'/ OИкс' | Sj ′/ Oy ′ | … | Sk ′/ Oz ′ |
| … | … | … | … | … |
| Sм | Sя"/ OИкс" | Sj ″/ Oz ″ | … | Sk ″/ Oz ″ |
Во втором случае одно из измерений указывает текущие состояния, а другое - следующие состояния. Пересечения строк / столбцов обозначают входы и (необязательно) выходы, связанные с переходами состояний.
Следующее состояние Текущее состояние | S1 | S2 | … | Sм |
|---|---|---|---|---|
| S1 | яя/ OИкс | — | … | — |
| S2 | — | — | … | яj/ Oу |
| … | … | … | … | … |
| Sм | — | яk/ Oz | … | — |
Другие формы
Одновременные переходы в нескольких конечных автоматах могут быть показаны в том, что по сути является n-мерной таблицей переходов состояний, в которой пары строк отображают (наборы) текущие состояния на следующие состояния.[1] Это альтернатива представлению связи между отдельными, взаимозависимыми конечными автоматами.
С другой стороны, отдельные таблицы использовались для каждого из переходов в одном конечном автомате: «таблицы И / ИЛИ»[2] похожи на неполные таблицы решений в котором решение для присутствующих правил неявно является активацией соответствующего перехода.
Пример
Пример таблицы переходов состояний вместе с соответствующими диаграмма состояний для конечного автомата приведено ниже:
Вход Текущее состояние | 0 | 1 |
|---|---|---|
| S1 | S2 | S1 |
| S2 | S1 | S2 |
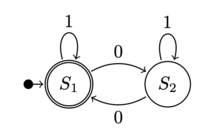 |
В таблице перехода состояний все возможные входные данные для конечного автомата перечислены по столбцам таблицы, а все возможные состояния перечислены по строкам. Если автомат находится в состоянии S1 (первая строка) и получает на входе 1 (второй столбец), автомат останется в состоянии S1. Теперь, если автомат находится в состоянии S1 и получит на входе 0 (первый столбец), автомат перейдет в состояние S2.
На диаграмме состояний первое обозначено стрелкой, идущей от S1 к S1 помечены цифрой 1, а последняя обозначена стрелкой от S1 к S2 с цифрой 0. Этот процесс можно описать статистически с помощью Цепи Маркова.
Для недетерминированный конечный автомат, ввод может привести к тому, что машина будет находиться более чем в одном состоянии, следовательно, ее недетерминизм. Это обозначается в таблице переходов состояний набором всех целевых состояний, заключенных в пару фигурных скобок {}. Пример таблицы переходов состояний вместе с соответствующей диаграммой состояний для недетерминированного конечного автомата приведен ниже:
Вход Текущее состояние | 0 | 1 |
|---|---|---|
| S1 | S2 | S1 |
| S2 | {S1, S2} | S2 |
 |
Если автомат находится в состоянии S2 и получает на входе 0, машина будет в двух состояниях одновременно, состояния S1 и S2.
Преобразования из / в диаграмму состояний
Можно нарисовать диаграмма состояний из таблицы переходов состояний. Ниже приводится последовательность простых шагов:
- Нарисуйте круги, чтобы обозначить данные состояния.
- Для каждого состояния просканируйте соответствующую строку и нарисуйте стрелку к целевому состоянию (ям). Если конечный автомат недетерминирован, для входного символа может быть несколько стрелок.
- Обозначьте состояние как начальное состояние. Начальное состояние дано в формальном определении конечного автомата.
- Обозначьте одно или несколько состояний как принимающее государство. Это также дается в формальном определении конечного автомата.
Смотрите также
Рекомендации
- ^ Брин, Майкл (2005), «Опыт использования упрощенного метода формальной спецификации для линейки коммерческих встроенных систем» (PDF), Журнал разработки требований, 10 (2): 161–172, CiteSeerX 10.1.1.60.5228, Дои:10.1007 / s00766-004-0209-1
- ^ Левесон, Нэнси; Хеймдал, Матс Пер Эрик; Хилдрет, Холли; Риз, Джон Дэймон (1994), «Технические требования к системам управления процессами» (PDF), IEEE Transactions по разработке программного обеспечения, 20 (9): 684–707, CiteSeerX 10.1.1.72.8657, Дои:10.1109/32.317428
дальнейшее чтение
- Майкл Сипсер: Введение в теорию вычислений. PWS Publishing Co., Бостон, 1997 г. ISBN 0-534-94728-X
