Конечный автомат - Википедия - Finite-state machine


А конечный автомат (FSM) или же конечный автомат (FSA, множественное число: автоматы), конечный автомат, или просто Государственный аппарат, является математическим модель вычисления. Это абстрактная машина который может быть ровно одним из конечного числа состояния в любой момент времени. FSM может переходить из одного состояния в другое в ответ на некоторые входы; переход из одного состояния в другое называется переход.[1] Конечный автомат определяется списком его состояний, его начального состояния и входов, запускающих каждый переход. Конечные автоматы бывают двух типов:детерминированные конечные автоматы и недетерминированные конечные автоматы.[2] Детерминированный конечный автомат может быть сконструирован эквивалентным любому недетерминированному.
Поведение конечных автоматов можно наблюдать на многих устройствах современного общества, которые выполняют заранее определенную последовательность действий в зависимости от последовательности событий, с которыми они представлены. Простые примеры торговые автоматы, которые выдают продукты при внесении правильной комбинации монет, лифты, чья последовательность остановок определяется этажами, запрошенными гонщиками, светофор, которые изменяют последовательность, когда машины ждут, и кодовые замки, которые требуют ввода последовательности чисел в правильном порядке.
Конечный автомат имеет меньшую вычислительную мощность, чем некоторые другие модели вычислений, такие как Машина Тьюринга.[3] Различие в вычислительной мощности означает, что есть вычислительные задачи, которые машина Тьюринга может выполнять, а конечный автомат - нет. Это потому, что конечный автомат объем памяти ограничено количеством состояний, которые у него есть. Конечные автоматы изучаются в более общей области: теория автоматов.
Пример: монетный турникет


Примером простого механизма, который можно смоделировать с помощью конечного автомата, является турникет.[4][5] Турникет, используемый для контроля доступа к метро и аттракционам, представляет собой ворота с тремя вращающимися рычагами на уровне пояса, одна из которых находится напротив входа. Первоначально руки заблокированы, блокируя вход, не позволяя посетителям пройти. Внесение монеты или жетон в прорези на турникете открывает рычаги, позволяя одному клиенту протолкнуться. После того, как покупатель проходит, рычаги снова блокируются, пока не будет вставлена другая монета.
Турникет, рассматриваемый как конечный автомат, имеет два возможных состояния: Заблокировано и Разблокирован.[4] Есть два возможных входа, которые влияют на его состояние: вставка монеты в слот (монета) и толкнув руку (толкать). В заблокированном состоянии нажатие на руку не имеет никакого эффекта; независимо от того, сколько раз ввод толкать дан, он остается в заблокированном состоянии. Положить монету - то есть дать машине монета input - сдвигает состояние с Заблокировано к Разблокирован. В разблокированном состоянии добавление дополнительных монет не имеет никакого эффекта; то есть, давая дополнительные монета input не меняет состояние. Однако покупатель проталкивает руки, давая понять толкать ввод, возвращает состояние к Заблокировано.
Конечный автомат турникета можно представить в виде таблица переходов между состояниями, показывая для каждого возможного состояния переходы между ними (на основе входных данных, данных машине) и выходы, возникающие в результате каждого входа:
Текущее состояние Вход Следующее состояние Выход Заблокировано монета Разблокирован Разблокирует турникет, чтобы клиент мог пройти. толкать Заблокировано Никто Разблокирован монета Разблокирован Никто толкать Заблокировано Когда клиент протолкнется, турникет запирается.
Конечный автомат турникета также можно представить в виде ориентированный граф называется диаграмма состояний (над). Каждое состояние представлено узел (круг). Края (стрелки) показывают переходы из одного состояния в другое. Каждая стрелка помечена входом, который запускает этот переход. Вход, который не вызывает изменения состояния (например, монета вклад в Разблокирован состояние) отображается круговой стрелкой, возвращающейся в исходное состояние. Стрелка в Заблокировано узел из черной точки указывает, что это начальное состояние.
Понятия и терминология
А государственный - это описание состояния системы, ожидающей выполнения переход. Переход - это набор действий, которые должны быть выполнены при выполнении условия или при получении события. Например, при использовании аудиосистемы для прослушивания радио (система находится в состоянии «радио») получение сообщения " следующий «стимул» приводит к переходу к следующей станции. Когда система находится в состоянии «CD», «следующий» стимул приводит к переходу к следующей дорожке. Одинаковые стимулы запускают разные действия в зависимости от текущего состояния.
В некоторых представлениях конечных автоматов также можно связать действия с состоянием:
- действие входа: выполнено при входе государство, и
- действие выхода: выполнено при выходе штат.
Представления

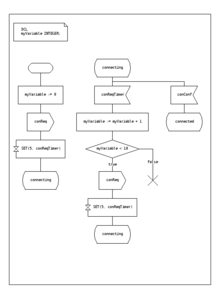
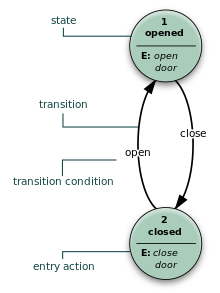
Таблица состояний / событий
Несколько таблица переходов между состояниями используются типы. Наиболее распространенное представление показано ниже: комбинация текущего состояния (например, B) и ввода (например, Y) показывает следующее состояние (например, C). Полная информация о действии не описана в таблице напрямую и может быть добавлена только с помощью сносок. Определение конечного автомата, включая полную информацию о действиях, возможно с использованием таблицы состояний (смотрите также виртуальный конечный автомат ).
Текущий государственный Вход | Состояние А | Состояние B | Состояние C |
|---|---|---|---|
| Вход X | ... | ... | ... |
| Вход Y | ... | Состояние C | ... |
| Вход Z | ... | ... | ... |
Конечные автоматы UML
В Единый язык моделирования имеет обозначение для описания конечных автоматов. Конечные автоматы UML преодолеть ограничения традиционных конечных автоматов, сохранив при этом их основные преимущества. Конечные автоматы UML представляют новые концепции иерархически вложенные состояния и ортогональные области, расширяя понятие действия. Конечные автоматы UML обладают характеристиками как Мучные машины и Машины Мура. Они поддерживают действия которые зависят как от состояния системы, так и от срабатывания мероприятие, как в машинах Мили, а также входные и выходные действия, которые связаны с состояниями, а не переходами, как в машинах Мура.[нужна цитата ]
Конечные автоматы SDL
В Спецификация и язык описания это стандарт от ITU который включает графические символы для описания действий при переходе:
- отправить событие
- получить событие
- запустить таймер
- отменить таймер
- запустить другой параллельный конечный автомат
- решение
SDL включает базовые типы данных, называемые «абстрактными типами данных», язык действий и семантику выполнения, чтобы сделать конечный автомат исполняемым.[нужна цитата ]
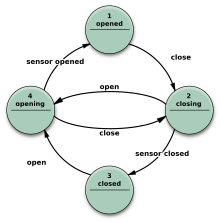
Диаграммы других состояний
Существует большое количество вариантов представления конечного автомата, такого как показанный на рисунке 3.
использование
В дополнение к их использованию в моделировании реактивных систем, представленных здесь, конечные автоматы важны во многих различных областях, включая электротехника, лингвистика, Информатика, философия, биология, математика, программирование видеоигр, и логика. Конечные автоматы - это класс автоматов, изучаемый в теория автоматов и теория вычислений.В информатике конечные автоматы широко используются при моделировании поведения приложений, проектировании аппаратные цифровые системы, программная инженерия, компиляторы, сетевые протоколы, а также изучение вычислений и языков.
Классификация
Конечные машины можно разделить на акцепторы, классификаторы, преобразователи и секвенсоры.[6]
Акцепторы


Акцепторы (также называемый детекторы или же распознаватели) производят двоичный вывод, указывая, принят ли полученный ввод. Каждое состояние акцептора либо принимая или же не принимающий. После получения всех входных данных, если текущее состояние является состоянием приема, вход принимается; в противном случае он отклоняется. Как правило, ввод - это последовательность символов (символы); действия не используются. Начальное состояние также может быть состоянием принятия, и в этом случае акцептор принимает пустую строку. Пример на рисунке 4 показывает акцептор, который принимает строку "nice". В этом акцепторе единственное принимающее состояние - это состояние 7.
Набор (возможно бесконечный) последовательностей символов, называемый формальный язык, это обычный язык если есть акцептор, который принимает точно тот набор. Например, набор двоичных строк с четным числом нулей является обычным языком (см. Рис. 5), а набор всех строк, длина которых является простым числом, - нет.[7]:18,71
Акцептор также можно описать как определение языка, который будет содержать каждую строку, принимаемую акцептором, но ни одну из отклоненных; этот язык принято акцептором. По определению, языки, принятые акцепторами, являются обычные языки.
Проблема определения языка, принятого данным акцептором, является примером проблема алгебраического пути - само по себе обобщение проблема кратчайшего пути в графы с ребрами, взвешенными элементами произвольной (произвольной) полукольцо.[8][9][жаргон ]
Пример состояния приема показан на рис. 5: a детерминированный конечный автомат (DFA), который определяет, двоичный входная строка содержит четное количество нулей.
S1 (который также является начальным состоянием) указывает состояние, в котором было введено четное количество нулей. S1 поэтому является принимающим государством. Этот акцептор завершит работу в состоянии принятия, если двоичная строка содержит четное количество нулей (включая любую двоичную строку, не содержащую нулей). Примеры строк, принимаемых этим акцептором: ε (в пустой строкой ), 1, 11, 11 ..., 00, 010, 1010, 10110 и т. Д.
Классификаторы
Классификаторы являются обобщением акцепторов, производящих п-арный выход, где п строго больше двух.[нужна цитата ]
Преобразователи

Преобразователи производить вывод на основе заданного ввода и / или состояния, используя действия. Они используются для приложений управления и в области компьютерная лингвистика.
В управляющих приложениях различают два типа:
- Машина Мура
- Конечный автомат использует только действия входа, т.е. выход зависит только от состояния. Преимущество модели Мура - упрощение поведения. Рассмотрим дверь лифта. Конечный автомат распознает две команды: «command_open» и «command_close», которые запускают изменение состояния. Действие входа (E :) в состоянии «Открытие» запускает двигатель, открывающий дверь, действие входа в состоянии «Закрытие» запускает двигатель в другом направлении, закрывая дверь. Состояния «Открыто» и «Закрыто» останавливают двигатель при полном открытии или закрытии. Они сигнализируют внешнему миру (например, другим конечным автоматам) о ситуации: «дверь открыта» или «дверь закрыта».
- Мучная машина
- Автомат также использует входные действия, т.е. выход зависит от входа и состояния. Использование автомата Мили часто приводит к уменьшению количества состояний. В примере на рисунке 7 показан автомат Мили, реализующий то же поведение, что и в примере Мура (поведение зависит от реализованной модели выполнения конечного автомата и будет работать, например, для виртуальный автомат но не для управляемый событиями автомат ). Есть два действия ввода (I :): «запустить двигатель, чтобы закрыть дверь, если приходит command_close» и «запустить двигатель в другом направлении, чтобы открыть дверь, если приходит command_open». Промежуточные состояния «открытие» и «закрытие» не показаны.
Секвенсоры
Секвенсоры (также называемый генераторы) являются подклассом акцепторов и преобразователей, которые имеют однобуквенный входной алфавит. Они производят только одну последовательность, которую можно рассматривать как выходную последовательность выходных сигналов приемника или преобразователя.[6]
Детерминизм
Еще одно различие между детерминированный (DFA ) и недетерминированный (NFA, GNFA ) автоматы. В детерминированном автомате каждое состояние имеет ровно один переход для каждого возможного входа. В недетерминированном автомате вход может привести к одному, более чем одному или отсутствию перехода для данного состояния. В конструкция электростанции Алгоритм может преобразовать любой недетерминированный автомат в (обычно более сложный) детерминированный автомат с идентичной функциональностью.
Конечный автомат только с одним состоянием называется «комбинаторным автоматом». Он разрешает действия только при переходе в Штат. Эта концепция полезна в тех случаях, когда требуется несколько конечных автоматов для совместной работы, и когда удобно рассматривать чисто комбинаторную часть как форму конечного автомата, подходящую для инструментов проектирования.[10]
Альтернативная семантика
Доступны и другие наборы семантики для представления конечных автоматов. Например, есть инструменты для моделирования и проектирования логики для встроенных контроллеров.[11] Они сочетаются иерархические машины состояний (которые обычно имеют более одного текущего состояния), потоковые графы и таблицы истинности на один язык, что приводит к другому формализму и набору семантики.[12] Эти диаграммы, как и оригинальные конечные автоматы Харела,[13] поддерживать иерархически вложенные состояния, ортогональные области, действия состояния и действия перехода.[14]
Математическая модель
В соответствии с общей классификацией найдены следующие формальные определения.
А детерминированный конечный автомат или же детерминированный конечный акцептор это пятиместный , куда:
- это вход алфавит (конечный непустой набор символов);
- - конечное непустое множество состояний;
- начальное состояние, элемент ;
- это функция перехода между состояниями: (в недетерминированный конечный автомат это было бы , т.е. вернет набор состояний);
- - множество конечных состояний, (возможно, пустое) подмножество .
Как для детерминированных, так и для недетерминированных автоматов принято допускать быть частичная функция, т.е. необязательно определять для каждой комбинации и . Если автомат находится в состоянии , следующий символ и не определено, то может объявить об ошибке (т.е. отклонить ввод). Это полезно в определениях общих конечных автоматов, но менее полезно при преобразовании машины. Некоторые алгоритмы в их стандартной форме могут потребовать общих функций.
Конечный автомат имеет ту же вычислительную мощность, что и Машина Тьюринга который ограничен таким образом, что его голова может выполнять только операции «чтения» и всегда должна двигаться слева направо. То есть каждый формальный язык, принятый конечным автоматом, принимается такой ограниченной машиной Тьюринга, и наоборот.[15]
А конечный преобразователь это шестерка , куда:
- это вход алфавит (конечный непустой набор символов);
- - выходной алфавит (конечный непустой набор символов);
- - конечное непустое множество состояний;
- начальное состояние, элемент ;
- это функция перехода между состояниями: ;
- - функция вывода.
Если функция вывода зависит от состояния и символа ввода () это определение соответствует Мили модель, и может быть смоделирована как Мучная машина. Если функция вывода зависит только от состояния () это определение соответствует Модель Мура, и может быть смоделирована как Машина Мура. Конечный автомат без функции вывода вообще известен как полуавтомат или же переходная система.
Если не принимать во внимание первый выходной символ машины Мура, , то его можно легко преобразовать в эквивалентную по выходу машину Мили, установив функцию вывода каждого перехода Мили (т. е. пометив каждый край) выходным символом, заданным для целевого состояния Мура. Обратное преобразование менее прямолинейно, поскольку состояние машины Мили может иметь разные выходные метки на входящих переходах (краях). Каждое такое состояние необходимо разделить на несколько состояний машины Мура, по одному для каждого выходного символа инцидента.[16]
Оптимизация
Оптимизация конечного автомата означает поиск машины с минимальным количеством состояний, выполняющей ту же функцию. Самый быстрый известный алгоритм, делающий это, - это Алгоритм минимизации Хопкрофта.[17][18] Другие методы включают использование таблица импликации, или Процедура редукции Мура. Кроме того, ациклические FSA можно минимизировать за линейное время.[19]
Выполнение
Аппаратные приложения

В цифровая схема, конечный автомат может быть построен с использованием программируемое логическое устройство, а Программируемый логический контроллер, логические ворота и шлепки или же реле. В частности, для аппаратной реализации требуется регистр для хранения переменных состояния, блок комбинационная логика который определяет переход состояния, и второй блок комбинационной логики, который определяет вывод конечного автомата. Одна из классических аппаратных реализаций - это Контроллер Richards.
В Машина Медведева, выход напрямую подключен к триггерам состояния, что минимизирует временную задержку между триггерами и выходом.[20][21]
Через кодирование состояния для малой мощности конечные автоматы могут быть оптимизированы для минимизации энергопотребления.
Программные приложения
Следующие концепции обычно используются для создания программных приложений с конечными автоматами:
- Программирование на основе автоматов
- Конечный автомат, управляемый событиями
- Виртуальный конечный автомат
- Паттерн государственного проектирования
Конечные машины и компиляторы
Конечные автоматы часто используются в внешний интерфейс компиляторов языков программирования. Такой интерфейс может включать в себя несколько конечных автоматов, реализующих лексический анализатор и синтаксический анализатор. Начиная с последовательности символов, лексический анализатор строит последовательность языковых токенов (таких как зарезервированные слова, литералы и идентификаторы), из которых синтаксический анализатор строит синтаксическое дерево. Лексический анализатор и парсер обрабатывают обычные и контекстно-свободные части грамматики языка программирования.[22]
Смотрите также
- Абстрактные машины состояний (КАК М)
- Искусственный интеллект (AI)
- Абстрактный язык конечных автоматов (AsmL)
- Модель поведения
- Коммуникационный конечный автомат
- Система контроля
- Контрольный стол
- Таблицы решений
- DEVS: Спецификация системы дискретных событий
- Расширенный конечный автомат (EFSM)
- Конечный автомат с каналом данных
- Скрытая марковская модель
- Маломощный синтез конечных автоматов
- Сеть Петри
- Выталкивающий автомат
- Квантовые конечные автоматы (QFA)
- Узнаваемый язык
- Полуавтомат
- Полугрупповое действие
- Последовательная логика
- Спецификация и язык описания
- Диаграмма состояний
- Государственный образец
- SCXML
- Моноид преобразования
- Переходный моноид
- Система перехода
- Дерево-автомат
- Машина Тьюринга
- Конечный автомат UML
- Инструменты диаграммы состояний YAKINDU
Рекомендации
- ^ Ван, Цзяцунь (2019). Формальные методы в компьютерных науках. CRC Press. п. 34. ISBN 978-1-4987-7532-8.
- ^ "Конечные машины - блестящая вики по математике и науке". brilliant.org. Получено 2018-04-14.
- ^ Белзер, Джек; Хольцман, Альберт Джордж; Кент, Аллен (1975). Энциклопедия компьютерных наук и технологий. 25. США: CRC Press. п. 73. ISBN 978-0-8247-2275-3.
- ^ а б Коши, Томас (2004). Дискретная математика с приложениями. Академическая пресса. п. 762. ISBN 978-0-12-421180-3.
- ^ Райт, Дэвид Р. (2005). «Конечные автоматы» (PDF). Примечания к классу CSC215. Веб-сайт Дэвида Р. Райта, Государственный университет Н. Каролины. Архивировано из оригинал (PDF) на 2014-03-27. Получено 2012-07-14.
- ^ а б Келлер, Роберт М. (2001). «Классификаторы, акцепторы, преобразователи и секвенсоры» (PDF). Информатика: от абстракции к реализации (PDF). Колледж Харви Мадда. п. 480.
- ^ Джон Э. Хопкрофт и Джеффри Д. Уллман (1979). Введение в теорию автоматов, языки и вычисления. Ридинг / Массачусетс: Эддисон-Уэсли. ISBN 978-0-201-02988-8.
- ^ Пули, Марк; Колас, Юрг (2011). Общий вывод: объединяющая теория автоматизированных рассуждений. Джон Вили и сыновья. Глава 6. Алгебры оценок для задач о путях, с. 223 в частности. ISBN 978-1-118-01086-0.
- ^ Яцек Йончи (июнь 2008 г.). «Алгебраические задачи о путях» (PDF). Архивировано из оригинал (PDF) на 2014-08-21. Получено 2014-08-20., п. 34
- ^ Брутчек, М., Бергер, С., Франке, М., Шварцбахер, А., Беккер, С .: Процедура структурного разделения для эффективного анализа ИС. IET IrishSignals and Systems Conference, (ISSC 2008), стр. 18–23. Голуэй, Ирландия, 18–19 июня 2008 г. [1]
- ^ "Тивари, А. (2002). Формальная семантика и методы анализа для моделей Simulink Stateflow" (PDF). sri.com. Получено 2018-04-14.
- ^ Хамон, Г. (2005). Денотационная семантика для Stateflow. Международная конференция по встроенному ПО. Джерси-Сити, Нью-Джерси: ACM. С. 164–172. CiteSeerX 10.1.1.89.8817.
- ^ "Харел, Д. (1987). Визуальный формализм для сложных систем. Наука компьютерного программирования, 231–274" (PDF). Архивировано из оригинал (PDF) на 2011-07-15. Получено 2011-06-07.
- ^ Алур Р., Канаде А., Рамеш С. и Шашидхар К. С. (2008). Символьный анализ для улучшения покрытия симуляцией моделей Simulink / Stateflow. Международная конференция по встроенному программному обеспечению (стр. 89–98). Атланта, Джорджия: ACM.
- ^ Блэк, Пол Э (12 мая 2008 г.). «Конечный автомат». Словарь алгоритмов и структур данных. НАС. Национальный институт стандартов и технологий. Архивировано из оригинал 13 октября 2018 г.. Получено 2 ноября 2016.
- ^ Андерсон, Джеймс Эндрю; Голова, Томас Дж. (2006). Теория автоматов в современных приложениях. Издательство Кембриджского университета. С. 105–108. ISBN 978-0-521-84887-9.
- ^ Хопкрофт, Джон Э. (1971). An п бревно п алгоритм минимизации состояний в конечном автомате (PDF) (Технический отчет). CS-TR-71-190. Stanford Univ.[постоянная мертвая ссылка ]
- ^ Алмейда, Марко; Морейра, Нельма; Рейс, Роджерио (2007). О производительности алгоритмов минимизации автоматов (PDF) (Технический отчет). DCC-2007-03. Porto Univ. Архивировано из оригинал (PDF) 17 января 2009 г.. Получено 25 июн 2008.
- ^ Ревуз, Д. (1992). «Минимизация ациклических автоматов в линейное время». Теоретическая информатика. 92: 181–189. Дои:10.1016/0304-3975(92)90142-3.
- ^ Кэслин, Хуберт (2008). "Биты Мили, Мура, Медведева и комбинаторные выходные биты". Проектирование цифровых интегральных схем: от архитектур СБИС до изготовления КМОП. Издательство Кембриджского университета. п. 787. ISBN 978-0-521-88267-5.
- ^ Слайды В архиве 18 января 2017 г. Wayback Machine, Синхронные конечные автоматы; Дизайн и поведение, Гамбургский университет прикладных наук, стр.18
- ^ Ахо, Альфред В.; Сетхи, Рави; Ульман, Джеффри Д. (1986). Компиляторы: принципы, методы и инструменты (1-е изд.). Эддисон-Уэсли. ISBN 978-0-201-10088-4.
дальнейшее чтение
Общий
- Сакарович, Жак (2009). Элементы теории автоматов. Перевод с французского Рувима Томаса. Издательство Кембриджского университета. ISBN 978-0-521-84425-3. Zbl 1188.68177.
- Вагнер, Ф., "Программное обеспечение для моделирования с помощью конечных автоматов: практический подход", Auerbach Publications, 2006 г., ISBN 0-8493-8086-3.
- МСЭ-Т, Рекомендация Z.100 Язык спецификации и описания (SDL)
- Самек, М., Практические диаграммы состояний на C / C ++, CMP Books, 2002, ISBN 1-57820-110-1.
- Самек, М., Практические диаграммы состояний UML на C / C ++, 2-е издание, Newnes, 2008, ISBN 0-7506-8706-1.
- Гарднер, Т., Расширенное управление состоянием, 2007
- Кассандрас, С., Лафортюн, С., "Введение в дискретные системы событий". Клювер, 1999 г., ISBN 0-7923-8609-4.
- Тимоти Кам, Синтез конечных автоматов: функциональная оптимизация. Kluwer Academic Publishers, Бостон, 1997 г., ISBN 0-7923-9842-4
- Вилла Тициано, Синтез конечных автоматов: логическая оптимизация. Kluwer Academic Publishers, Бостон, 1997 г., ISBN 0-7923-9892-0
- Кэрролл, Дж., Лонг, Д., Теория конечных автоматов с введением в формальные языки. Prentice Hall, Englewood Cliffs, 1989.
- Кохави, З., Теория переключений и конечных автоматов. Макгроу-Хилл, 1978.
- Гилл, А., Введение в теорию конечных автоматов. МакГроу-Хилл, 1962 год.
- Гинзбург, С., Введение в математическую теорию машин. Аддисон-Уэсли, 1962.
Конечные автоматы (теория автоматов) в теоретической информатике
- Арбиб, Майкл А. (1969). Теории абстрактных автоматов (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Prentice-Hall, Inc. ISBN 978-0-13-913368-8.
- Bobrow, Леонард S .; Арбиб, Майкл А. (1974). Дискретная математика: прикладная алгебра для компьютерных и информационных наук (1-е изд.). Филадельфия: W. B. Saunders Company, Inc. ISBN 978-0-7216-1768-8.
- Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc., Каталог карточек Библиотеки Конгресса, номер 67-25924.
- Булос, Джордж; Джеффри, Ричард (1999) [1989]. Вычислимость и логика (3-е изд.). Кембридж, Англия: Издательство Кембриджского университета. ISBN 978-0-521-20402-6.
- Брукшир, Дж. Гленн (1989). Теория вычислений: формальные языки, автоматы и сложность. Редвуд-Сити, Калифорния: Benjamin / Cummings Publish Company, Inc. ISBN 978-0-8053-0143-4.
- Дэвис, Мартин; Сигал, Рон; Вейкер, Элейн Дж. (1994). Вычислимость, сложность, языки и логика: основы теоретической информатики (2-е изд.). Сан-Диего: Academic Press, Harcourt, Brace & Company. ISBN 978-0-12-206382-4.
- Хопкрофт, Джон; Ульман, Джеффри (1979). Введение в теорию автоматов, языки и вычисления (1-е изд.). Месса для чтения: Эддисон-Уэсли. ISBN 978-0-201-02988-8.
- Хопкрофт, Джон Э .; Мотвани, Раджив; Ульман, Джеффри Д. (2001). Введение в теорию автоматов, языки и вычисления (2-е изд.). Месса для чтения: Эддисон-Уэсли. ISBN 978-0-201-44124-6.
- Хопкин, Дэвид; Мосс, Барбара (1976). Автоматы. Нью-Йорк: Эльзевир Северная Голландия. ISBN 978-0-444-00249-5.
- Козен, Декстер К. (1997). Автоматы и вычислимость (1-е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-94907-9.
- Льюис, Гарри Р.; Пападимитриу, Христос Х. (1998). Элементы теории вычислений (2-е изд.). Река Аппер Сэдл, Нью-Джерси: Прентис-Холл. ISBN 978-0-13-262478-7.
- Линц, Питер (2006). Формальные языки и автоматы (4-е изд.). Садбери, Массачусетс: Джонс и Бартлетт. ISBN 978-0-7637-3798-6.
- Минский, Марвин (1967). Вычисления: конечные и бесконечные машины (1-е изд.). Нью-Джерси: Прентис-Холл.
- Пападимитриу, Христос (1993). Вычислительная сложность (1-е изд.). Эддисон Уэсли. ISBN 978-0-201-53082-7.
- Пиппенгер, Николас (1997). Теории вычислимости (1-е изд.). Кембридж, Англия: Издательство Кембриджского университета. ISBN 978-0-521-55380-3.
- Роджер, Сьюзен; Финли, Томас (2006). JFLAP: пакет интерактивных формальных языков и автоматов (1-е изд.). Садбери, Массачусетс: Джонс и Бартлетт. ISBN 978-0-7637-3834-1.
- Сипсер, Майкл (2006). Введение в теорию вычислений (2-е изд.). Бостон Масса: технология курса Томсона. ISBN 978-0-534-95097-2.
- Вуд, Дерик (1987). Теория вычислений (1-е изд.). Нью-Йорк: Harper & Row, Publishers, Inc. ISBN 978-0-06-047208-5.
Абстрактные конечные автоматы в теоретической информатике
- Гуревич, Юрий (июль 2000 г.). "Последовательные абстрактные конечные автоматы захватывают последовательные алгоритмы" (PDF). Транзакции ACM по вычислительной логике. 1 (1): 77–111. CiteSeerX 10.1.1.146.3017. Дои:10.1145/343369.343384. S2CID 2031696.
Машинное обучение с использованием алгоритмов конечного состояния
- Митчелл, Том М. (1997). Машинное обучение (1-е изд.). Нью-Йорк: WCB / McGraw-Hill Corporation. ISBN 978-0-07-042807-2.
Аппаратная инженерия: минимизация состояний и синтез последовательных схем
- Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc., Каталог карточек Библиотеки Конгресса, номер 67-25924.
- Бут, Тейлор Л. (1971). Цифровые сети и компьютерные системы (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc. ISBN 978-0-471-08840-0.
- Маккласки, Э. Дж. (1965). Введение в теорию коммутационных схем (1-е изд.). Нью-Йорк: McGraw-Hill Book Company, Inc. Каталог карточек Библиотеки Конгресса № 65-17394.
- Хилл, Фредрик Дж .; Петерсон, Джеральд Р. (1965). Введение в теорию коммутационных схем (1-е изд.). Нью-Йорк: Книжная компания Макгроу-Хилл. Каталог карточек Библиотеки Конгресса, номер 65-17394.
Конечные цепные процессы Маркова
- "Мы можем придумать Цепь Маркова как процесс, который последовательно проходит через набор состояний s1, s2, …, sр. … Если он в состоянии sя он переходит к следующей остановке, чтобы указать sj с вероятностью пij. Эти вероятности могут быть представлены в виде матрицы перехода »(Кемени (1959), стр. 384).
Конечные цепные марковские процессы также известны как подсдвиги конечного типа.
- Бут, Тейлор Л. (1967). Последовательные машины и теория автоматов (1-е изд.). Нью-Йорк: John Wiley and Sons, Inc., Каталог карточек Библиотеки Конгресса, номер 67-25924.
- Кемени, Джон Дж .; Миркил, Хэзлтон; Снелл, Дж. Лори; Томпсон, Джеральд Л. (1959). Конечные математические структуры (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Прентис-Холл, Инк. Каталог карточек Библиотеки Конгресса, номер 59-12841. Глава 6 «Конечные цепи Маркова».
внешняя ссылка
- Конечные автоматы в Керли
- Моделирование поведения простого ИИ с помощью конечного автомата Пример использования в видеоиграх
- Бесплатный онлайн-словарь по вычислительной технике описание конечных автоматов
- Словарь алгоритмов и структур данных NIST описание конечных автоматов
- Краткий обзор типов конечных автоматов, сравнивая теоретические аспекты конечных автоматов Мили, Мура, Харела и UML.




















