Дерево-автомат - Tree automaton

Для другого понятия древовидного автомата см. автомат для прогулки по деревьям.

А древовидный автомат это тип Государственный аппарат. Древовидные автоматы имеют дело с древовидные структуры, а не струны более обычных конечных автоматов.

Следующая статья посвящена автоматам ветвящихся деревьев, которые соответствуют регулярные языки деревьев.

Как и классические автоматы, конечные древовидные автоматы (FTA) могут быть либо детерминированный автомат или нет. В зависимости от того, как автомат обрабатывает входное дерево, конечные древовидные автоматы могут быть двух типов: (а) снизу вверх, (б) сверху вниз. Это важный вопрос, поскольку, хотя недетерминированные (ND) нисходящие и восходящие древовидные автоматы ND эквивалентны по выразительной мощности, детерминированные нисходящие автоматы строго менее мощны, чем их детерминированные восходящие аналоги, поскольку свойства дерева определяемые детерминированными автоматами дерева сверху вниз, могут зависеть только от свойств пути. (Детерминированные восходящие древовидные автоматы так же мощны, как и ND-деревья.)

Определения

А восходящий конечный древовидный автомат над F определяется как кортеж (Q, F, Qж, Δ), где Q это набор состояний, F это ранжированный алфавит (т. е. алфавит, символы которого имеют связанный арность ), Qж ⊆ Q - набор конечных состояний, а Δ - набор правила перехода формы ж(q1(Икс1),...,qп(Иксп)) → q(ж(Икс1,...,Иксп)), для п-ари ж ∈ F, q, qя ∈ Q, и Икся переменные, обозначающие поддеревья. То есть члены Δ являются правилами перезаписи из узлов, чьи дочерние корни являются состояниями, в узлы, корнями которых являются состояния. Таким образом, состояние узла выводится из состояний его дочерних узлов.

Для п= 0, то есть для постоянного символа ж, приведенное выше определение правила перехода гласит ж() → q(ж()); часто пустые скобки опускаются для удобства: ж → q(жПоскольку эти правила перехода для константных символов (листьев) не требуют состояния, никаких явно определенных начальных состояний не требуется. Восходящий древовидный автомат запускается на основной срок над F, начиная со всех его листьев одновременно и двигаясь вверх, связывая состояние выполнения с Q с каждым подтермом. термин принимается, если его корень связан с принимающим состоянием из Qж.[1]

А нисходящий конечный древовидный автомат над F определяется как кортеж (Q, F, Qя, Δ), с двумя отличиями от автоматов дерева снизу вверх. Первый, Qя ⊆ Q, множество его начальных состояний заменяет Qж; во-вторых, его правила перехода ориентированы наоборот:q(ж(Икс1,...,Иксп)) → ж(q1(Икс1),...,qп(Иксп)), для п-ари ж ∈ F, q, qя ∈ Q, и Икся переменные, обозначающие поддеревья, то есть элементы Δ здесь представляют собой правила перезаписи от узлов, корни которых являются состояниями, до узлов, чьи дочерние корни являются состояниями. Нисходящий автомат запускается в некоторых из своих начальных состояний в корне и движется вниз по ветвям дерева. дерево, индуктивно ассоциируя состояние с каждым подтермом. Дерево принимается, если каждая ветвь может быть пройдена таким образом.[2]

Древовидный автомат называется детерминированный (сокращенно DFTA) если никакие два правила из Δ не имеют одинаковой левой части; иначе это называется недетерминированный (NFTA).[3] Недетерминированные древовидные автоматы сверху вниз обладают той же выразительной способностью, что и недетерминированные автоматы снизу вверх;[4] правила перехода просто меняются местами, и конечные состояния становятся начальными состояниями.

Напротив, детерминированный нисходящие древовидные автоматы[5] менее эффективны, чем их восходящие аналоги, потому что в детерминированном древовидном автомате нет двух правил перехода с одинаковой левой частью. Для древовидных автоматов правила перехода - это правила перезаписи; а для нисходящих узлов левая сторона будет родительскими узлами. Следовательно, детерминированный нисходящий древовидный автомат сможет проверять только те свойства дерева, которые истинны во всех ветвях, потому что выбор состояния для записи в каждую дочернюю ветвь определяется в родительском узле, не зная содержимого дочерних ветвей. .

Примеры

Автомат снизу вверх, принимающий булевы списки

Использование раскраски для различения членов F и Q, и используя ранжированный алфавит F={ ложный,правда,ноль,минусы(.,.) }, с участием минусы имеющий арность 2 и все остальные символы, имеющие арность 0, восходящий древовидный автомат, принимающий набор всех конечных списков логических значений, может быть определен как (Q, F, Qж, Δ) с Q={ Bool,BList }, Qж={ BList }, и Δ, состоящее из правил

ложный→Bool(ложный)(1),
правда→Bool(правда)(2),
ноль→BList(ноль)(3), и
минусы(Bool(Икс1),BList(Икс2))→BList(минусы(Икс1,Икс2))      (4).

В этом примере правила можно интуитивно понять как присвоение каждому термину его типа снизу вверх; например Правило (4) можно прочитать как «Термин минусы(Икс1,Икс2) имеет тип BList, предоставлена Икс1 и Икс2 имеет тип Bool и BListсоответственно ". Допустимый прогон примера

минусы(ложный,минусы(правда,ноль))
⇒минусы(ложный,минусы(правда,BList(ноль)))по (3)
⇒минусы(ложный,минусы(Bool(правда),BList(ноль)))по (2)
⇒минусы(ложный,BList(минусы(правда,ноль)))по (4)
⇒минусы(Bool(ложный),BList(минусы(правда,ноль)))по (1)
⇒BList(минусы(ложный,минусы(правда,ноль)))      по (4), принято.

Ср. вывод того же члена из регулярной древовидной грамматики, соответствующей автомату, показанной на Грамматика регулярных деревьев # Примеры.

Отклоняющий пример запуска

минусы(ложный,правда)
⇒минусы(ложный,Bool(правда))по (1)
⇒минусы(Bool(ложный),Bool(правда))      согласно (2), никакие другие правила не применяются.

Интуитивно это соответствует термину минусы(ложный,правда) не очень хорошо типизирован.

Нисходящий автомат, принимающий числа, кратные 3, в двоичной системе счисления

(А)(В)(С)(D)
Строка
грамматика
правила		Строка
автомат
переходы		Дерево
автомат
переходы		Дерево
грамматика
правила
0
1
2
3
4
5
6
S0→ε
S0→0 S0
S0→1 S1
S1→0 S2
S1→1 S0
S2→0 S1
S2→1 S2
 
δ (S0,0)= S0
δ (S0,1)= S1
δ (S1,0)= S2
δ (S1,1)= S0
δ (S2,0)= S1
δ (S2,1)= S2
S0(ноль)→ноль
S0(0(Икс))→0(S0(Икс))
S0(1(Икс))→1(S1(Икс))
S1(0(Икс))→0(S2(Икс))
S1(1(Икс))→1(S0(Икс))
S2(0(Икс))→0(S1(Икс))
S2(1(Икс))→1(S2(Икс))
S0→ноль
S0→0(S0)
S0→1(S1)
S1→0(S2)
S1→1(S0)
S2→0(S1)
S2→1(S2)
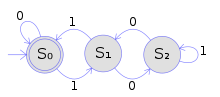Детерминированный конечный (струнный) автомат прием кратных 3 в двоичной системе счисления

Используя ту же раскраску, что и выше, этот пример показывает, как древовидные автоматы обобщают обычные строковые автоматы. Конечный детерминированный строковый автомат, показанный на рисунке, принимает все строки двоичных цифр, которые обозначают кратное 3. Детерминированный конечный автомат # Формальное определение, это определяется:

  • набор Q государств, являющихся { S0, S1, S2 },
  • входной алфавит - { 0, 1 },
  • начальное состояние S0,
  • набор конечных состояний { S0 }, и
  • переходы такие, как показано в столбце (B) таблицы.

В настройке древовидного автомата входной алфавит изменяется таким образом, что символы 0 и 1 являются унарными и нулевыми символами, скажем ноль используется для листьев дерева. Например, двоичная строка "110"в строковом автомате настройка соответствует термину"1(1(0(ноль))) "в настройке древовидного автомата; таким образом, строки могут быть обобщены до деревьев или терминов. Нисходящий конечный древовидный автомат, принимающий набор всех терминов, соответствующих кратным 3 в двоичной строковой нотации, определяется следующим образом:

  • набор Q штатов все еще { S0, S1, S2 },
  • ранжированный входной алфавит { 0, 1, ноль }, с участием Arity(0)=Arity(1) = 1 и Arity(ноль) = 0, как объяснялось,
  • набор начальных состояний { S0 }, и
  • переходы такие, как показано в столбце (C) таблицы.

Например, дерево "1(1(0(ноль))) "принимает следующий прогон древовидного автомата:

S0(1(1(0(ноль))))
⇒1(S1(1(0(ноль))))на 2
⇒1(1(S0(0(ноль))))по 4
⇒1(1(0(S0(ноль))))на 1
⇒1(1(0(ноль)))      0

Напротив, термин "1(0(ноль)) "приводит к следующему недопустимому запуску автомата:

⇒ S0(1(0(ноль)))
⇒1(S1(0(ноль))))на 2
⇒1(0(S2(ноль))))      на 3, дальнейшие правила не применяются

Поскольку нет других начальных состояний, кроме S0 чтобы запустить автомат, термин "1(0(ноль)) "не принимается древовидным автоматом.

Для сравнения в столбцах (A) и (D) таблицы приведены значения (справа) обычная (строковая) грамматика, а регулярная древовидная грамматика соответственно, каждый из которых принимает тот же язык, что и его автоматный аналог.

Свойства

Узнаваемость

Для восходящего автомата основной термин т (то есть дерево) считается принятым, если существует редукция, начинающаяся с т и заканчивается q(т), где q это конечное состояние. Для нисходящего автомата наземный термин т принимается, если существует сокращение, начинающееся с q(т) и заканчивается на т, где q это начальное состояние.

Язык дерева L(А) принято, или признанный, древовидным автоматом А это набор всех основных условий, принятых А. Набор основных условий узнаваемый если существует древовидный автомат, который его принимает.

Линейное (то есть сохраняющее арность) гомоморфизм деревьев сохраняет узнаваемость.[6]

Полнота и редукция

Недетерминированный конечный древовидный автомат - это полный если существует хотя бы одно правило перехода для каждой возможной комбинации состояний символа. q является доступный если существует основной термин т такое, что существует редукция от т к q(тNFTA - это уменьшенный если доступны все его состояния.[7]

Лемма о накачке

Каждый достаточно большой[8] основной срок т на узнаваемом древовидном языке L может быть вертикально трехчастным[9] такое, что произвольное повторение ("накачка") средней части сохраняет полученный член в L.[10][11]

Для языка всех конечных списков логических значений из приведенного выше примера все термины, превышающие предел высоты k= 2 можно прокачать, так как они должны содержать вхождение минусы. Например,

минусы(ложный,минусы(правда,ноль)),
минусы(ложный,минусы(ложный,минусы(правда,ноль))),
минусы(ложный,минусы(ложный,минусы(ложный,минусы(правда,ноль)))), ...

все принадлежат этому языку.

Закрытие

Класс распознаваемых древовидных языков замкнут относительно объединения, дополнения и пересечения.[12]

Теорема Майхилла – Нероде

Сравнение на множестве всех деревьев по ранжированному алфавиту F является отношение эквивалентности такой, что ты1 ≡ v1 и и тып ≡ vп подразумевает ж(ты1,...,тып) ≡ ж(v1,...,vп), для каждого ж ∈ FОн имеет конечный индекс, если число его классов эквивалентности конечно.

Для данного древовидного языка L, сравнение можно определить как ты ≡L v если C[ты] ∈ L ⇔ C[v] ∈ L для каждого контекста C.

В Теорема Майхилла – Нероде для древовидного автомата утверждает, что следующие три утверждения эквивалентны:[13]

  1. L это узнаваемый древовидный язык
  2. L является объединением некоторых классов эквивалентности конгруэнции конечного индекса
  3. отношение ≡L является конгруэнцией конечного индекса

Смотрите также

Заметки

  1. ^ Comon et al. 2008 г., разд. 1.1, п. 20.
  2. ^ Comon et al. 2008 г., разд. 1.6, п. 38.
  3. ^ Comon et al. 2008 г., разд. 1.1, п. 23.
  4. ^ Comon et al. 2008 г., разд. 1.6, теорема 1.6.1, с. 38.
  5. ^ В строгом смысле детерминированные нисходящие автоматы не определяются Comon et al. (2008) но они там используются (раздел 1.6, предложение 1.6.2, стр. 38). Они принимают класс языков деревьев с замкнутым путем (раздел 1.8, упражнение 1.6, стр. 43-44).
  6. ^ Понятие в Comon et al. (2008 г., разд. 1.4, теорема 1.4.3, с. 31-32) гомоморфизма деревьев является более общим, чем в статье "гомоморфизм деревьев ".
  7. ^ Comon et al. 2008 г., разд. 1.1, п. 23-24.
  8. ^ Формально: рост (т) > k, с участием k > 0 зависит только от L, не на т
  9. ^ Формально: контекст есть C[.], нетривиальный контекст C’[.], И основной термин ты такой, что т = C[C’[ты]]. "Контекст" C[.] - дерево с одной дырой (или, соответственно, терм с одним вхождением одной переменной). Контекст называется «тривиальным», если дерево состоит только из дырочного узла (или, соответственно, если термин является просто переменной). Обозначение C[т] означает результат вставки дерева т в дыру C[.] (или, соответственно, создание экземпляра переменная для т). Comon et al. 2008 г., п. 17 дает формальное определение.
  10. ^ Формально: C[C’п[ты]] ∈ L для всех п ≥ 0. Обозначения Cп[.] означает результат наложения п копии C[.] один в другой, ср. Comon et al. 2008 г., п. 17.
  11. ^ Comon et al. 2008 г., разд. 1.2, п. 29.
  12. ^ Comon et al. 2008 г., разд. 1.3, теорема 1.3.1, с. 30.
  13. ^ Comon et al. 2008 г., разд. 1.5, стр. 36.

использованная литература

  • Комон, Юбер; Дауше, Макс; Гиллерон, Реми; Жакемар, Флоран; Лужие, Денис; Лёдинг, Кристоф; Тисон, Софи; Томмази, Марк (ноябрь 2008 г.). Методы и приложения древовидных автоматов (PDF). Получено 11 февраля 2014.
  • Хосоя, Харуо (4 ноября 2010 г.). Основы обработки XML: подход древовидных автоматов. Издательство Кембриджского университета. ISBN  978-1-139-49236-2.CS1 maint: ref = harv (ссылка на сайт)

внешние ссылки

Реализации

  • Граппа - библиотеки ранговых и неранжированных древовидных автоматов (OCaml)
  • Тимбук - инструменты для анализа достижимости и расчетов древовидных автоматов (OCaml)
  • СМЕРТЕЛЬНЫЙ - библиотека для работы с конечными деревьями и хедж-автоматами (Java)
  • Библиотека автоматов дерева с машинной проверкой (Изабель [OCaml, SML, Haskell])
  • ВАТА - библиотека для эффективного управления недетерминированными древовидными автоматами (C ++)