Феномен Стокса - Stokes phenomenon

В комплексный анализ то Феномен Стокса, обнаруженный Г. Г. Стоукс (1847, 1858 ), заключается в том, что асимптотика функций может различаться в разных областях комплексной плоскости. Эти области ограничены Линия Стокса или же антистоксовы линии.

Линии Стокса и антистоксовы линии

Несколько сбивает с толку то, что математики и физики используют термины «линия Стокса» и «линия антистокса» по-разному. Линии, первоначально изученные Стоксом, - это то, что некоторые математики называют антистоксовыми линиями, а физики - линиями Стокса. (Эти термины также используются в оптике для несвязанных Линии Стокса и антистоксовы линии в Рамановское рассеяние ). В этой статье используется соглашение физиков, которое исторически является более точным и, похоже, становится все более распространенным среди математиков. Олвер (1997) рекомендует термин «главная кривая» для (физических) антистоксовых линий.

Неформально антистоксовы линии - это примерно то место, где какой-то член асимптотического разложения изменяется с возрастающего на убывающее (и, следовательно, может демонстрировать чисто колебательное поведение), а линии Стокса - это линии, вдоль которых какой-то член максимально быстро приближается к бесконечности или к нулю. Антистоксовы линии ограничивают области, в которых функция демонстрирует определенную асимптотику. Линии Стокса и антистоксовы линии не уникальны и на самом деле не имеют точного определения в целом, потому что область, в которой функция имеет заданное асимптотическое поведение, является несколько расплывчатым понятием. Однако линии обычно имеют четко определенные направления в существенных особенностях функции, и иногда существует естественный выбор этих линий следующим образом. Асимптотическое разложение функции часто задается линейной комбинацией функций вида ж(z) е^{±грамм(z)} для функций ж и грамм. Линии Стокса тогда можно принять за нули мнимой части грамм, а антистоксовы линии - нули действительной части грамм. (Это не совсем канонично, потому что к грамм, изменяя линии.) Если линии определены таким образом, то они ортогональны в местах пересечения, если только грамм имеет кратный ноль.

В качестве тривиального примера функция sinh (z) имеет две области Re (z)> 0 и Re (z) <0, где она асимптотична e^z/ 2 и −e^−z/ 2. Таким образом, антистоксова линия может быть принята за мнимую ось, а линия Стокса - за действительную ось. С равным успехом можно принять линию Стокса как любую линию данной мнимой части; эти варианты отличаются только вертикальным сдвигом, показывая, что для линии Стокса нет канонического выбора.

Пример: функция Эйри

В Функция Эйри Ай (Икс) является одним из двух решений простого дифференциального уравнения

{ Displaystyle у '' - ху = 0, ,}

которые часто бывает полезно аппроксимировать для многих значений Икс - в том числе комплексные значения. Для больших Икс данного аргумента решение можно аппроксимировать линейной комбинацией функций

{ displaystyle { frac {e ^ { pm { frac {2} {3}} x ^ {3/2}}} {x ^ {1/4}}}.}

Однако линейная комбинация должна измениться как аргумент Икс передает определенные значения, потому что эти приближения являются многозначными функциями, но функция Эйри однозначна. Например, если мы рассматриваем предел Икс как большие и реальные, и хотели бы аппроксимировать функцию Эйри как для положительных, так и для отрицательных значений, мы бы обнаружили, что

Сюжет Ай (Икс) красным цветом и Bi (Икс) в синем

{ displaystyle { begin {align} mathrm {Ai} (x) & {} sim { frac {e ^ {- { frac {2} {3}} x ^ {3/2}}} { 2 { sqrt { pi}} , x ^ {1/4}}} mathrm {Ai} (-x) & {} sim { frac { sin ({ frac {2} { 3}} x ^ {3/2} + { frac {1} {4}} pi)} {{ sqrt { pi}} , x ^ {1/4}}} end { выровнено}}}

Линии Стокса и антистоксовы линии для функции Эйри

которые представляют собой два очень разных выражения. Произошло то, что по мере того, как мы увеличили аргумент из Икс от 0 до пи (вращая его вокруг верхней полуплоскости комплекса) мы пересекли антистоксову линию, которая в данном случае находится на ${ displaystyle operatorname {arg} , x = pi / 3}$ . На этой антистоксовой линии коэффициент ${ displaystyle { frac {e ^ {- { frac {2} {3}} x ^ {3/2}}} {x ^ {1/4}}}}$ вынужден прыгнуть. Коэффициент ${ displaystyle { frac {e ^ {+ { frac {2} {3}} x ^ {3/2}}} {x ^ {1/4}}}}$ может прыгнуть на эту строку, но не вынужден; он может постепенно меняться как arg Икс изменяется от π / 3 до π, поскольку не определяется в этой области.

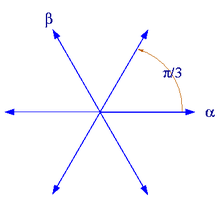
Имеются три антистоксовы линии с аргументами π / 3, π. –Π / 3 и три линии Стокса с аргументами 2π / 3, 0. –2π / 3.

Пример: линейные дифференциальные уравнения второго порядка

Пример функции Эйри может быть обобщен на широкий класс линейных дифференциальных уравнений второго порядка следующим образом. Стандартными заменами переменных уравнение второго порядка часто можно изменить к одному из следующих видов:

{ displaystyle { frac {d ^ {2} w} {dz ^ {2}}} = f (z) w}

куда ж голоморфна в односвязной области и ш является решением дифференциального уравнения. Тогда в некоторых случаях Метод ВКБ дает асимптотическое приближение для ш как линейная комбинация функций вида

{ displaystyle { frac { exp { pm int _ {a} ^ {z} { sqrt {f (z ')}} , dz'}} {f (z) ^ {1/4} }}}

для некоторой постоянной а. (Выбор разных значений а эквивалентно выбору различных коэффициентов в линейной комбинации.) Антистоксовы линии и линии Стокса тогда являются нулями действительной и мнимой частей соответственно

{ displaystyle int _ {a} ^ {z} { sqrt {f (z)}} , dz.}

Если а простой нуль ж затем локально ж похоже ${ Displaystyle F '(а) (г-а)}$ . Решения будут локально вести себя как функции Эйри; у них будет три линии Стокса и три линии антистокса, встречающиеся в а.

Феномен Стокса - Stokes phenomenon

Содержание

Линии Стокса и антистоксовы линии

Пример: функция Эйри

Пример: линейные дифференциальные уравнения второго порядка

Рекомендации