Тестовые функции для оптимизации - Test functions for optimization
В прикладной математике тестовые функции, известный как искусственные пейзажи, полезны для оценки характеристик алгоритмов оптимизации, таких как:
- Скорость сходимости.
- Точность.
- Надежность.
- Общая производительность.
Здесь представлены некоторые тестовые функции с целью дать представление о различных ситуациях, с которыми приходится сталкиваться алгоритмам оптимизации при решении подобных проблем. В первой части представлены некоторые целевые функции для случаев одноцелевой оптимизации. Во второй части тестовые функции с соответствующими фронтами Парето для многокритериальная оптимизация даны задачи (СС).
Искусственные ландшафты, представленные здесь для задач одноцелевой оптимизации, взяты из Bäck,[1] Haupt et al.[2] и из программного обеспечения Rody Oldenhuis.[3] Учитывая количество задач (всего 55), здесь представлены лишь некоторые. Полный список тестовых функций можно найти на сайте Mathworks.[4]
Тестовые функции, используемые для оценки алгоритмов MOP, были взяты из Deb,[5] Binh et al.[6] и Бинь.[7] Вы можете скачать программное обеспечение, разработанное Деб,[8] который реализует процедуру NSGA-II с ГА или программу, размещенную в Интернете,[9] который реализует процедуру NSGA-II с ES.
Приведены просто общий вид уравнения, график целевой функции, границы переменных объекта и координаты глобальных минимумов.
Тестовые функции для одноцелевой оптимизации
| имя | участок | Формула | Глобальный минимум | Поиск домена |
|---|---|---|---|---|
| Функция Растригина |  | |||
| Функция Экли | 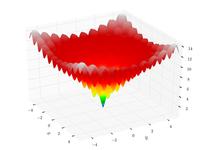 | |||
| Сфера функция | 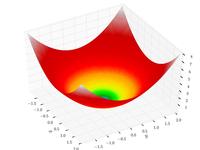 | , | ||
| Функция Розенброка | 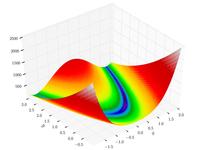 | , | ||
| Функция Била |  | |||
| Функция Гольдштейна – Прайса | 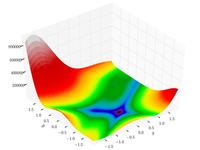 | |||
| Функция будки | 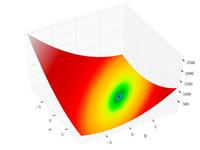 | |||
| Функция Букина N.6 | 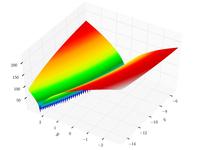 | , | ||
| Функция Матьяса | 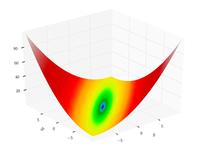 | |||
| Функция Леви N.13 | 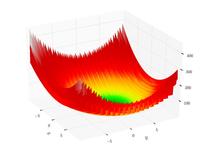 | |||
| Функция Химмельблау | 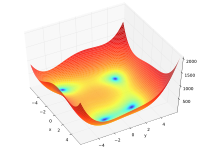 | |||
| Функция трехгорбого верблюда | 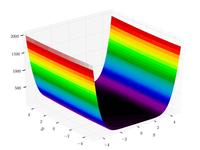 | |||
| Функция EASOM | 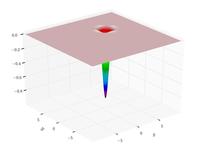 | |||
| Функция кросс-лотка | 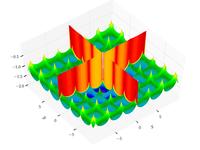 | |||
| Функция Eggholder [10] | 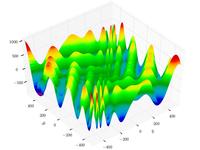 | |||
| Табличная функция Гёльдера | 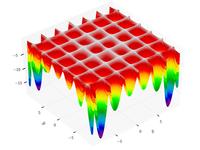 | |||
| Функция Маккормика | 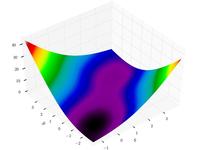 | , | ||
| Функция Шаффера N. 2 | 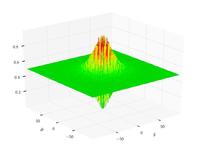 | |||
| Функция Шаффера N. 4 | 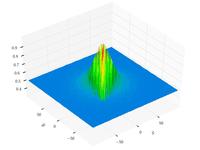 | |||
| Функция Стыблинского – Танга | 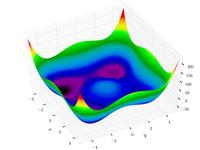 | , .. |
Тестовые функции для оптимизации с ограничениями
| имя | участок | Формула | Глобальный минимум | Поиск домена |
|---|---|---|---|---|
| Функция Розенброка с кубикой и линией[11] |  | , подвергается: | , | |
| Функция Розенброка, привязанная к диску[12] | 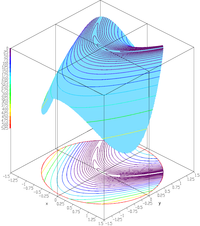 | , подвергается: | , | |
| Функция птицы Мишры - с ограничениями[13][14] | 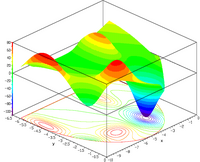 | , подвергается: | , | |
| Функция Таунсенда (измененная)[15] |  | , подвергается:где: т = Атан2 (х, у) | , | |
| Функция Симионеску[16] |  | , подвергается: |
Тестовые функции для многокритериальной оптимизации
[требуется дальнейшее объяснение ]
| имя | участок | Функции | Ограничения | Поиск домена |
|---|---|---|---|---|
| Функция Бина и Корна:[6] | 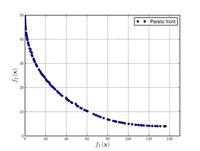 | , | ||
| Функция Чанконга и Хаймса:[17] |  | |||
| Функция Фонсека – Флеминга:[18] | 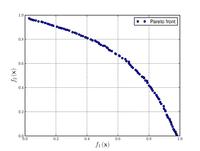 | , | ||
| Тестовая функция 4:[7] | ![Функция тестирования 4. [7]](http://upload.wikimedia.org/wikipedia/commons/thumb/3/3c/Test_function_4_-_Binh.pdf/page1-200px-Test_function_4_-_Binh.pdf.jpg) | |||
| Функция Курсаве:[19] | 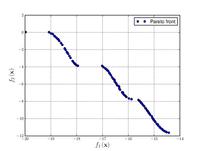 | , . | ||
| Функция Шаффера № 1:[20] | 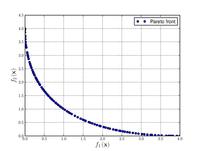 | . Ценности от к были успешно использованы. Более высокие значения увеличивают сложность проблемы. | ||
| Функция Шаффера № 2: |  | . | ||
| Две целевые функции Полони: | 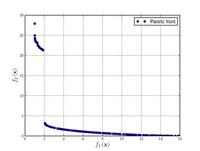 | |||
| Функция Цицлера – Деба – Тиле № 1:[21] |  | , . | ||
| Функция Цицлера – Деба – Тиле № 2:[21] | 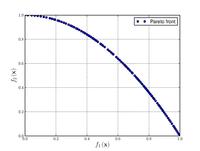 | , . | ||
| Функция Цицлера – Деба – Тиле № 3:[21] | 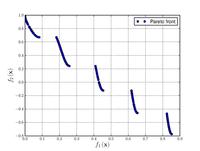 | , . | ||
| Функция Цицлера – Деба – Тиле № 4:[21] | 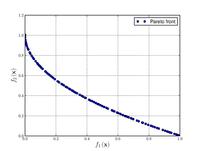 | , , | ||
| Функция Цицлера – Деба – Тиле № 6:[21] |  | , . | ||
| Функции Осички и Кунду:[22] | 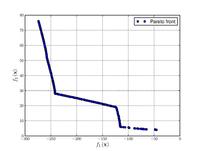 | , , . | ||
| Функция CTP1 (2 переменные):[5][23] | ![Функция CTP1 (2 переменные). [5]](http://upload.wikimedia.org/wikipedia/commons/thumb/d/d4/CTP1_function_%282_variables%29.pdf/page1-200px-CTP1_function_%282_variables%29.pdf.jpg) | . | ||
| Проблема с Constr-Ex:[5] | ![Проблема Constr-Ex. [5]](http://upload.wikimedia.org/wikipedia/commons/thumb/6/6f/Constr-Ex_problem.pdf/page1-200px-Constr-Ex_problem.pdf.jpg) | , | ||
| Функция Viennet: | 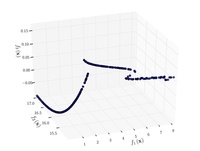 | . |
Смотрите также
использованная литература
- ^ Бэк, Томас (1995). Эволюционные алгоритмы в теории и практике: стратегии эволюции, эволюционное программирование, генетические алгоритмы. Оксфорд: Издательство Оксфордского университета. п. 328. ISBN 978-0-19-509971-3.
- ^ Хаупт, Рэнди Л. Хаупт, Сью Эллен (2004). Практические генетические алгоритмы с CD-Rom (2-е изд.). Нью-Йорк: Дж. Вили. ISBN 978-0-471-45565-3.
- ^ Oldenhuis, Роди. «Множество тестовых функций для глобальных оптимизаторов». Математические работы. Получено 1 ноября 2012.
- ^ Ортис, Жилберто А. "Стратегии эволюции (ES)". Математические работы. Получено 1 ноября 2012.
- ^ а б c d е Деб, Калянмой (2002) Многокритериальная оптимизация с использованием эволюционных алгоритмов (Repr. Ed.). Чичестер [u.a.]: Уайли. ISBN 0-471-87339-X.
- ^ а б Бинь Т. и Корн У. (1997) MOBES: стратегия многокритериальной эволюции для задач оптимизации с ограничениями. В: Труды Третьей международной конференции по генетическим алгоритмам. Чехия. стр. 176–182
- ^ а б c Бинь Т. (1999) Многокритериальный эволюционный алгоритм. Учебные кейсы. Технический отчет. Институт автоматики и связи. Барлебен, Германия
- ^ Деб К. (2011) Программное обеспечение для многоцелевого кода NSGA-II на C. Доступно по URL: https://www.iitk.ac.in/kangal/codes.shtml
- ^ Ортис, Жилберто А. «Многоцелевая оптимизация с использованием ЭС как эволюционного алгоритма». Математические работы. Получено 1 ноября 2012.
- ^ Ванарет К. (2015) Гибридизация интервальных методов и эволюционных алгоритмов для решения сложных оптимизационных задач. Кандидатская диссертация. Ecole Nationale de l'Aviation Civile. Национальный политехнический институт Тулузы, Франция.
- ^ Simionescu, P.A .; Бил, Д. (29 сентября - 2 октября 2002 г.). Новые концепции в графической визуализации целевых функций (PDF). ASME 2002 Международные конструкторские технические конференции и Конференция "Компьютеры и информация в машиностроении". Монреаль, Канада. стр. 891–897. Получено 7 января 2017.
- ^ «Решите ограниченную нелинейную задачу - MATLAB и Simulink». www.mathworks.com. Получено 2017-08-29.
- ^ "Проблема с птицами (с ограничениями) | Интеграция с Phoenix". Архивировано 29 декабря 2016 года.. Получено 2017-08-29.CS1 maint: BOT: статус исходного URL-адреса неизвестен (ссылка на сайт)
- ^ Мишра, Судханшу (2006). «Некоторые новые тестовые функции для глобальной оптимизации и производительности метода роя отталкивающих частиц». Бумага MPRA.
- ^ Таунсенд, Алекс (январь 2014). «Оптимизация с ограничениями в Chebfun». chebfun.org. Получено 2017-08-29.
- ^ Симионеску, П.А. (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.
- ^ Чанконг, Вира; Хаймс, Яков Ю. (1983). Принятие многокритериальных решений. Теория и методология. ISBN 0-444-00710-5.
- ^ Fonseca, C.M .; Флеминг, П. Дж. (1995). «Обзор эволюционных алгоритмов многокритериальной оптимизации». Evol Comput. 3 (1): 1–16. CiteSeerX 10.1.1.50.7779. Дои:10.1162 / evco.1995.3.1.1.
- ^ Ф. Курсаве, "Вариант эволюционных стратегий векторной оптимизации," в PPSN I, Vol 496 Lect Notes in Comput Sc. Springer-Verlag, 1991, стр. 193–197.
- ^ Шаффер, Дж. Дэвид (1984). Множественная объективная оптимизация с использованием генетических алгоритмов с векторной оценкой. Материалы Первой Междунар. Конференция по генетическим алгоритмам / Под ред. G.J.E Grefensette, J.J. Лоуренс Эрлбраум (Кандидат наук). Университет Вандербильта. OCLC 20004572.
- ^ а б c d е Деб, Калян; Thiele, L .; Лауманнс, Марко; Цитцлер, Эккарт (2002). «Масштабируемые тестовые задачи многокритериальной оптимизации». Proc. Конгресса IEEE 2002 г. по эволюционным вычислениям. 1: 825–830. Дои:10.1109 / CEC.2002.1007032. ISBN 0-7803-7282-4.
- ^ Osyczka, A .; Кунду, С. (1 октября 1995 г.). «Новый метод решения обобщенных задач многокритериальной оптимизации с использованием простого генетического алгоритма». Структурная оптимизация. 10 (2): 94–99. Дои:10.1007 / BF01743536. ISSN 1615-1488.
- ^ Jimenez, F .; Гомес-Скармета, А. Ф .; Sanchez, G .; Деб, К. (май 2002 г.). «Эволюционный алгоритм многоцелевой оптимизации с ограничениями». Труды Конгресса по эволюционным вычислениям 2002 г. CEC'02 (Кат. № 02TH8600). 2: 1133–1138. Дои:10.1109 / CEC.2002.1004402. ISBN 0-7803-7282-4.

![f ( mathbf {x}) = An + sum _ {i = 1} ^ {n} left [x_ {i} ^ {2} -A cos (2 pi x_ {i}) right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1aa1c38ee739ca9cf4582867d74d469df4676cbc)



![{ displaystyle f (x, y) = - 20 exp left [-0.2 { sqrt {0,5 left (x ^ {2} + y ^ {2} right)}} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f00d1325d65d088f8ae6a96137e62021107921d)
![{ Displaystyle - ехр влево [0,5 влево ( соз 2 пи х + соз 2 пи у вправо) вправо] + е + 20}](https://wikimedia.org/api/rest_v1/media/math/render/svg/565ef43958a50fb0ef473bdd46e30bfc725604a7)






![{ displaystyle f ({ boldsymbol {x}}) = sum _ {i = 1} ^ {n-1} left [100 left (x_ {i + 1} -x_ {i} ^ {2}) right) ^ {2} + left (1-x_ {i} right) ^ {2} right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/64863353dcdea2f0ed049cec3aea0a4284d4916a)





![{ displaystyle f (x, y) = left [1+ left (x + y + 1 right) ^ {2} left (19-14x + 3x ^ {2} -14y + 6xy + 3y ^ { 2} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d020ed324ff07759faf17591157771b0e2cdf07)
![{ displaystyle left [30+ left (2x-3y right) ^ {2} left (18-32x + 12x ^ {2} + 48y-36xy + 27y ^ {2} right) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/32e562da4f3219f9d66e059441c59e1d299e8557)



















![{ displaystyle f (x, y) = - 0,0001 left [ left | sin x sin y exp left ( left | 100 - { frac { sqrt {x ^ {2} + y ^ { 2}}} { pi}} right | right) right | +1 right] ^ {0.1}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d591ae9bcf2feae162cd00398d78bb6870c82946)










![{ displaystyle f (x, y) = 0,5 + { frac { sin ^ {2} left (x ^ {2} -y ^ {2} right) -0,5} { left [1 + 0,001 влево (x ^ {2} + y ^ {2} right) right] ^ {2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/995008c6f10a14b44dac568cc544efb7d5ddd631)
![{ Displaystyle е (х, у) = 0,5 + { гидроразрыва { соз ^ {2} влево [ грех влево ( влево | х ^ {2} -y ^ {2} вправо | вправо) right] -0.5} { left [1 + 0,001 left (x ^ {2} + y ^ {2} right) right] ^ {2}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2458c352c0c0524648d8ef713bcea4e80df32fd8)











![{ Displaystyle е (х, у) = грех (у) е ^ { влево [(1- соз х) ^ {2} вправо]} + соз (х) е ^ { влево [(1 - sin y) ^ {2} right]} + (xy) ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7987d4a794d861e7ccd0795265841d3ca172cfae)




![{ Displaystyle f (x, y) = - [ соз ((x-0,1) y)] ^ {2} -x sin (3x + y)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8dac25f97d0b720512d72c313000d5fb5c7d033a)
![{ displaystyle x ^ {2} + y ^ {2} < left [2 cos t - { frac {1} {2}} cos 2t - { frac {1} {4}} cos 3t - { frac {1} {8}} cos 4t right] ^ {2} + [2 sin t] ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57168b192e685c6144e3a9527b12087ac7cb11b4)




![{ displaystyle x ^ {2} + y ^ {2} leq left [r_ {T} + r_ {S} cos left (n arctan { frac {x} {y}} right) вправо] ^ {2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1fc42adcc2095ed0c0214a74799db7ee2fac9923)










![{ displaystyle { text {Minimize}} = { begin {case} f_ {1} left ({ boldsymbol {x}} right) = 1- exp left [- sum _ {i = 1 } ^ {n} left (x_ {i} - { frac {1} { sqrt {n}}} right) ^ {2} right] f_ {2} left ({ boldsymbol { x}} right) = 1- exp left [- sum _ {i = 1} ^ {n} left (x_ {i} + { frac {1} { sqrt {n}}} справа) ^ {2} right] end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3113203c5d455e0e1e6397d57094e80e527b34ba)




![{ displaystyle { text {Minimize}} = { begin {cases} f_ {1} left ({ boldsymbol {x}} right) = sum _ {i = 1} ^ {2} left [ -10 exp left (-0.2 { sqrt {x_ {i} ^ {2} + x_ {i + 1} ^ {2}}} right) right] & f_ {2} left ({ boldsymbol {x}} right) = sum _ {i = 1} ^ {3} left [ left | x_ {i} right | ^ {0.8} +5 sin left (x_ {i} ^ {3} right) right] end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/aeb9856144d9869aae4254892ece0fe894dfc152)








![{ displaystyle { text {Minimize}} = { begin {cases} f_ {1} left (x, y right) = left [1+ left (A_ {1} -B_ {1} left) (x, y right) right) ^ {2} + left (A_ {2} -B_ {2} left (x, y right) right) ^ {2} right] f_ { 2} left (x, y right) = left (x + 3 right) ^ {2} + left (y + 1 right) ^ {2} end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ee5df22af124899c1e268325017ea64e517b51e)










![{ displaystyle { text {Minimize}} = { begin {case} f_ {1} left ({ boldsymbol {x}} right) = 1- exp left (-4x_ {1} right) sin ^ {6} left (6 pi x_ {1} right) f_ {2} left ({ boldsymbol {x}} right) = g left ({ boldsymbol {x}} right) h left (f_ {1} left ({ boldsymbol {x}} right), g left ({ boldsymbol {x}} right) right) g left ({ boldsymbol {x}} right) = 1 + 9 left [{ frac { sum _ {i = 2} ^ {10} x_ {i}} {9}} right] ^ {0,25} h left (f_ {1} left ({ boldsymbol {x}} right), g left ({ boldsymbol {x}} right) right) = 1- left ({ frac {f_ { 1} left ({ boldsymbol {x}} right)} {g left ({ boldsymbol {x}} right)}} right) ^ {2} end {case}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f03bdd2b0c7a5af33b0a0fc385f9a9c021635d6e)














