В численные методы , уменьшение общей вариации (TVD) является собственностью определенных дискретизация схемы, используемые для решения гиперболические уравнения в частных производных . Наиболее заметное применение этого метода в вычислительная гидродинамика . Концепция TVD была представлена Ами Хартен .[1]
Уравнение модели В системах, описанных уравнения в частных производных , например следующие гиперболические уравнение переноса ,
∂ ты ∂ т + а ∂ ты ∂ Икс = 0 , {displaystyle {frac {partial u} {partial t}} + a {frac {partial u} {partial x}} = 0,} то полное изменение (ТВ) дается
Т V ( ты ( ⋅ , т ) ) = ∫ | ∂ ты ∂ Икс | d Икс , {displaystyle TV (u (cdot, t)) = int left | {frac {partial u} {partial x}} ight | mathrm {d} x,} а полное изменение для дискретного случая равно,
Т V ( ты п ) = Т V ( ты ( ⋅ , т п ) ) = ∑ j | ты j + 1 п − ты j п | . {displaystyle TV (u ^ {n}) = TV (u (cdot, t ^ {n})) = sum _ {j} left | u_ {j + 1} ^ {n} -u_ {j} ^ {n } право |.} куда ты j п = ты ( Икс j , т п ) {displaystyle u_ {j} ^ {n} = u (x_ {j}, t ^ {n})}
Численный метод называется общее уменьшение вариации (TVD) если,
Т V ( ты п + 1 ) ≤ Т V ( ты п ) . {displaystyle TVleft (u ^ {n + 1} ight) leq TVleft (u ^ {n} ight).} Характеристики Численная схема называется сохраняющей монотонность, если сохраняются следующие свойства:
Если ты п {displaystyle u ^ {n}} ты п + 1 {displaystyle u ^ {n + 1}} Хартен 1983 доказали следующие свойства численной схемы:
Применение в CFD В Вычислительная гидродинамика , TVD-схема используется для получения более точных прогнозов ударной волны без каких-либо вводящих в заблуждение колебаний при изменении переменной поля « ϕ {displaystyle phi} Δ Икс {displaystyle Delta x} центральная разностная схема , схема против ветра , гибридная разностная схема , и схема степенного закона дает ложные предсказания шока. Схема TVD позволяет более точно прогнозировать ударную нагрузку на грубых сетках, экономя время вычислений, а поскольку схема сохраняет монотонность, в решении отсутствуют паразитные колебания.
Дискретизация Рассмотрим стационарное одномерное уравнение диффузии конвекции,
∇ ⋅ ( ρ ты ϕ ) = ∇ ⋅ ( Γ ∇ ϕ ) + S ϕ {displaystyle abla cdot (ho mathbf {u} phi), = abla cdot (Gamma abla phi) + S_ {phi};} куда ρ {displaystyle ho} ты {displaystyle mathbf {u}} ϕ {displaystyle phi} Γ {displaystyle Gamma} S ϕ {displaystyle S_ {phi}} ϕ {displaystyle phi}
Выполняя баланс потока этого свойства относительно контрольного объема, мы получаем,
∫ А п ⋅ ( ρ ты ϕ ) d А = ∫ А п ⋅ ( Γ ∇ ϕ ) d А + ∫ C V S ϕ d V {displaystyle int _ {A} mathbf {n} cdot (ho mathbf {u} phi), mathrm {d} A = int _ {A} mathbf {n} cdot (Gamma abla phi), mathrm {d} A + int _ {CV} S_ {phi}, математика {d} V} {displaystyle;} Здесь п {displaystyle mathbf {n}}
Игнорируя исходный член, уравнение сводится к следующему:
( ρ ты ϕ А ) р − ( ρ ты ϕ А ) л = ( Γ А ∂ ϕ ∂ Икс ) р − ( Γ А ∂ ϕ ∂ Икс ) л {displaystyle (ho mathbf {u} phi A) _ {r} - (ho mathbf {u} phi A) _ {l} = left (Gamma A {frac {partial phi} {partial x}} ight) _ {r } -левый (Gamma A {frac {partial phi} {partial x}} ight) _ {l}} Картинка, показывающая контрольный объем со скоростями на гранях, узлах и расстоянии между ними, где «P» - узел в центре.
Предполагая
∂ ϕ ∂ Икс = δ ϕ δ Икс {displaystyle {frac {partial phi} {partial x}} = {frac {delta phi} {delta x}}} А р = А л , {displaystyle A_ {r} = A_ {l},} Уравнение сводится к
( ρ ты ϕ ) р − ( ρ ты ϕ ) л = ( Γ δ Икс δ ϕ ) р − ( Γ δ Икс δ ϕ ) л . {displaystyle (ho mathbf {u} phi) _ {r} - (ho mathbf {u} phi) _ {l}, = left ({frac {Gamma} {delta x}} delta phi ight) _ {r} - left ({frac {Gamma} {delta x}} delta phi ight) _ {l}.} Сказать,
F р = ( ρ ты ) р ; F л = ( ρ ты ) л ; {displaystyle F_ {r} = (ho mathbf {u}) _ {r}; qquad F_ {l} = (ho mathbf {u}) _ {l};} D л = ( Γ δ Икс ) л ; D р = ( Γ δ Икс ) р ; {displaystyle D_ {l} = left ({frac {Gamma} {delta x}} ight) _ {l}; qquad D_ {r} = left ({frac {Gamma} {delta x}} ight) _ {r}) ;} На рисунке:
δ ϕ р = ϕ р − ϕ п ; δ Икс р = Икс п р ; {displaystyle delta phi _ {r} = phi _ {R} -phi _ {P}; qquad delta x_ {r} = x_ {PR};} δ ϕ л = ϕ п − ϕ L ; δ Икс л = Икс L п ; {displaystyle delta phi _ {l} = phi _ {P} -phi _ {L}; qquad delta x_ {l} = x_ {LP};} Уравнение становится,
F р ϕ р − F л ϕ л = D р ( ϕ р − ϕ п ) − D л ( ϕ п − ϕ L ) ; {displaystyle F_ {r} phi _ {r} -F_ {l} phi _ {l} = D_ {r} (phi _ {R} -phi _ {P}) - D_ {l} (phi _ {P} -phi _ {L});} Так же
уравнение неразрывности должно быть выполнено в одной из эквивалентных ему форм для этой задачи:
( ρ ты ) р − ( ρ ты ) л = 0 ⟺ F р − F л = 0 ⟺ F р = F л = F . {displaystyle (ho mathbf {u}) _ {r} - (ho mathbf {u}) _ {l}, = 0 Longleftrightarrow F_ {r} -F_ {l} = 0 Longleftrightarrow F_ {r} = F_ {l} = F.} Предполагая диффузионность является однородным свойством и равным шагом сетки, можно сказать
Γ л = Γ р ; δ Икс L п = δ Икс п р = δ Икс , {displaystyle Gamma _ {l} = Gamma _ {r}; qquad delta x_ {LP} = delta x_ {PR} = delta x,} мы получили
D л = D р = D . {displaystyle D_ {l} = D_ {r} = D.} Далее уравнение сводится к
( ϕ р − ϕ л ) ⋅ F = D ⋅ ( ϕ р − 2 ϕ п + ϕ L ) . {displaystyle (phi _ {r} -phi _ {l}) cdot F = Dcdot (phi _ {R} -2phi _ {P} + phi _ {L}).} Вышеприведенное уравнение можно записать как
( ϕ р − ϕ л ) ⋅ п = ( ϕ р − 2 ϕ п + ϕ L ) {displaystyle (phi _ {r} -phi _ {l}) cdot P = (phi _ {R} -2phi _ {P} + phi _ {L})} куда
п {displaystyle P} это
Число Пекле п = F D = ρ ты δ Икс Γ . {displaystyle P = {frac {F} {D}} = {frac {ho mathbf {u} delta x} {Gamma}}.} Схема TVD Схема уменьшения общей вариации[2] [3] ϕ р {displaystyle phi _ {r}} ϕ л {displaystyle phi _ {l}}
ϕ р ⋅ п = 1 2 ( п + | п | ) [ ж р + ϕ р + ( 1 − ж р + ) ϕ L ] + 1 2 ( п − | п | ) [ ж р − ϕ п + ( 1 − ж р − ) ϕ р р ] {displaystyle phi _ {r} cdot P = {frac {1} {2}} (P + | P |) [f_ {r} ^ {+} phi _ {R} + (1-f_ {r} ^ {+ }) phi _ {L}] + {frac {1} {2}} (P- | P |) [f_ {r} ^ {-} phi _ {P} + (1-f_ {r} ^ {- }) phi _ {RR}]} ϕ л ⋅ п = 1 2 ( п + | п | ) [ ж л + ϕ п + ( 1 − ж л + ) ϕ L L ] + 1 2 ( п − | п | ) [ ж л − ϕ L + ( 1 − ж л − ) ϕ р ] {displaystyle phi _ {l} cdot P = {frac {1} {2}} (P + | P |) [f_ {l} ^ {+} phi _ {P} + (1-f_ {l} ^ {+ }) phi _ {LL}] + {frac {1} {2}} (P- | P |) [f_ {l} ^ {-} phi _ {L} + (1-f_ {l} ^ {- }) phi _ {R}]} Где п {displaystyle P} ж {displaystyle f}
ж = ж ( ϕ U − ϕ U U ϕ D − ϕ U U ) {displaystyle f = fleft ({frac {phi _ {U} -phi _ {UU}} {phi _ {D} -phi _ {UU}}} ight)} куда U {displaystyle U} U U {displaystyle UU} U {displaystyle U} D {displaystyle D}
Обратите внимание, что ж + {displaystyle f ^ {+}} ж − {displaystyle f ^ {-}}
ж р + является функцией ( ϕ п − ϕ L ϕ р − ϕ L ) , ж р − является функцией ( ϕ р − ϕ р р ϕ п − ϕ р р ) , ж л + является функцией ( ϕ L − ϕ L L ϕ п − ϕ L L ) , и ж л − является функцией ( ϕ п − ϕ р ϕ L − ϕ р ) . {displaystyle {egin {align} & f_ {r} ^ {+} {ext {является функцией}} left ({dfrac {phi _ {P} -phi _ {L}} {phi _ {R} -phi _ {L}}} ight), [10pt] & f_ {r} ^ {-} {ext {является функцией}} left ({dfrac {phi _ {R} -phi _ {RR}} {phi _ { P} -phi _ {RR}}} ight), [10pt] & f_ {l} ^ {+} {ext {является функцией}} left ({dfrac {phi _ {L} -phi _ {LL} } {phi _ {P} -phi _ {LL}}} ight), {ext {and}} [10pt] & f_ {l} ^ {-} {ext {является функцией}} left ({dfrac { phi _ {P} -phi _ {R}} {phi _ {L} -phi _ {R}}} ight) .end {выровнено}}} Если поток положительный, то число Пекле п {displaystyle P} ( п − | п | ) = 0 {displaystyle (P- | P |) = 0} ж − {displaystyle f ^ {-}} ϕ р {displaystyle phi _ {r}} ϕ л {displaystyle phi _ {l}} п {displaystyle P} ( п + | п | ) = 0 {displaystyle (P + | P |) = 0} ж + {displaystyle f ^ {+}} ϕ р {displaystyle phi _ {r}} ϕ р {displaystyle phi _ {r}}
Поэтому он учитывает значения свойств в зависимости от направления потока, а с помощью взвешенных функций пытается достичь монотонности решения, тем самым обеспечивая результаты без ложных ударов.
Ограничения Монотонные схемы привлекательны для решения инженерных и научных задач, потому что они не дают нефизических решений. Теорема Годунова доказывает, что линейные схемы, сохраняющие монотонность, имеют точность не более первого порядка. Линейные схемы более высокого порядка, хотя и более точны для гладких решений, не являются TVD и имеют тенденцию вносить паразитные колебания (покачивания) там, где возникают разрывы или удары. Чтобы преодолеть эти недостатки, различные высокое разрешение , нелинейный были разработаны методы, часто использующие ограничители потока / наклона .
Смотрите также Рекомендации ^ Хартен, Ами (1983), "Схемы высокого разрешения для гиперболических законов сохранения", J. Comput. Phys. , 49 (2): 357–393, Дои :10.1016/0021-9991(83)90136-5 , HDL :2060/19830002586 ^ Versteeg, H.K .; Малаласекера, В. (2007). Введение в вычислительную гидродинамику: метод конечных объемов (2-е изд.). Харлоу: Прентис Холл. ISBN 9780131274983 ^ Блазек, Иржи (2001). Вычислительная гидродинамика: принципы и приложения (1-е изд.). Лондон: Эльзевьер. ISBN 9780080430096 дальнейшее чтение Хирш, К. (1990), Численный расчет внутренних и внешних потоков , Том 2, Wiley. Лэйни, К. Б. (1998), Вычислительная газовая динамика , Cambridge University Press. Торо, Э. Ф. (1999), Решатели Римана и численные методы гидродинамики , Springer-Verlag. Таннехилл, Дж. К., Андерсон, Д.А. и Плетчер Р. Х. (1997), Вычислительная механика жидкости и теплопередача , 2-е изд., Тейлор и Фрэнсис. Весселинг, П. (2001), Принципы вычислительной гидродинамики , Springer-Verlag. Анил В. Дата Введение в вычислительную гидродинамику , Cambridge University Press. 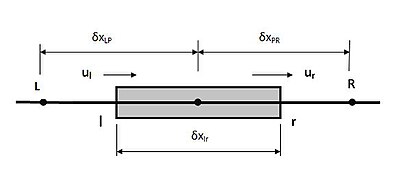




































![{displaystyle phi _ {r} cdot P = {frac {1} {2}} (P + | P |) [f_ {r} ^ {+} phi _ {R} + (1-f_ {r} ^ {+ }) phi _ {L}] + {frac {1} {2}} (P- | P |) [f_ {r} ^ {-} phi _ {P} + (1-f_ {r} ^ {- }) phi _ {RR}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dd8afd1eace057eb3b6452db18641aa87582a5b)
![{displaystyle phi _ {l} cdot P = {frac {1} {2}} (P + | P |) [f_ {l} ^ {+} phi _ {P} + (1-f_ {l} ^ {+ }) phi _ {LL}] + {frac {1} {2}} (P- | P |) [f_ {l} ^ {-} phi _ {L} + (1-f_ {l} ^ {- }) phi _ {R}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dec1cf62a6a6b4da1907d3d7aa52356efc4bf698)







![{displaystyle {egin {align} & f_ {r} ^ {+} {ext {является функцией}} left ({dfrac {phi _ {P} -phi _ {L}} {phi _ {R} -phi _ {L}}} ight), [10pt] & f_ {r} ^ {-} {ext {является функцией}} left ({dfrac {phi _ {R} -phi _ {RR}} {phi _ { P} -phi _ {RR}}} ight), [10pt] & f_ {l} ^ {+} {ext {является функцией}} left ({dfrac {phi _ {L} -phi _ {LL} } {phi _ {P} -phi _ {LL}}} ight), {ext {and}} [10pt] & f_ {l} ^ {-} {ext {является функцией}} left ({dfrac { phi _ {P} -phi _ {R}} {phi _ {L} -phi _ {R}}} ight) .end {выровнено}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/35ac4699e1448f23095b1a1c45899b99636aec7b)

