Нечеткие множества и системы типа 2 - Type-2 fuzzy sets and systems

Нечеткие множества и системы типа 2 обобщить стандарт Нечеткие множества типа 1 и системы так что можно справиться с большей неопределенностью. С самого начала создания нечетких множеств критика высказывалась по поводу того факта, что функция принадлежности нечеткого множества типа 1 не имеет связанной с ней неопределенности, что, кажется, противоречит слову нечеткий, поскольку это слово имеет оттенок неопределенности. Итак, что делать, когда есть неуверенность в значении функции принадлежности? Ответ на этот вопрос дал в 1975 году изобретатель нечетких множеств, Лотфи А. Заде[1], когда он предложил более сложные виды нечетких множеств, первое из которых он назвал «нечетким множеством типа 2». Нечеткое множество типа 2 позволяет нам включить неопределенность в отношении функции принадлежности в теорию нечетких множеств и является способом ответить на вышеупомянутую критику нечетких множеств типа 1. И, если нет неопределенности, то нечеткое множество типа 2 сокращается до нечеткого множества типа 1, что аналогично уменьшению вероятности до детерминизма, когда непредсказуемость исчезает.

Нечеткие системы типа 1 работают с фиксированным функция принадлежности, а в нечетких системах второго типа функция принадлежности колеблется. Нечеткое множество определяет, как входные значения преобразуются в нечеткие переменные.[2]

Обзор

Чтобы символически различать нечеткое множество типа 1 и нечеткое множество типа 2, над символом нечеткого множества помещается символ тильды; Итак, A обозначает нечеткое множество типа 1, тогда как Ã обозначает сопоставимое нечеткое множество типа 2. Когда последнее сделано, результирующее нечеткое множество типа 2 называется «общим нечетким множеством типа 2» (чтобы отличать его от специального интервального нечеткого множества типа 2).

Заде не остановился на нечетких множествах типа 2, потому что в той статье 1976 г.[1] он также обобщил все это на тип -п нечеткие множества. В данной статье рассматриваются только нечеткие множества типа 2, поскольку они являются следующий шаг в логической прогрессии от типа 1 к типуп нечеткие множества, где п = 1, 2,…. Хотя некоторые исследователи начинают исследовать нечеткие множества выше типа 2, по состоянию на начало 2009 года эта работа находится в зачаточном состоянии.

Рис. 1. Функция принадлежности общего нечеткого множества типа 2 трехмерна. Показано поперечное сечение одного среза третьего измерения. Это сечение, как и все другие, находится на FOU. Только граница сечения используется для описания функции принадлежности нечеткого множества общего типа 2. Показан заполненным в художественных целях.

Функция принадлежности общего нечеткого множества типа 2, Ã, является трехмерной (рис. 1), где третье измерение - это значение функции принадлежности в каждой точке ее двумерной области, которая называется ее "следом". неопределенности »(ФОУ).

Для нечеткого множества интервального типа 2 это значение третьего измерения везде одинаково (например, 1), что означает, что никакой новой информации не содержится в третьем измерении нечеткого множества интервального типа 2. Итак, для такого набора третье измерение игнорируется, и для его описания используется только FOU. Именно по этой причине интервальное нечеткое множество типа 2 иногда называют неопределенность первого порядка модель нечеткого множества, в то время как нечеткое множество общего типа 2 (с его полезным третьим измерением) иногда называют неопределенность второго порядка модель нечеткого множества.

Рис. 2. FOU для интервального нечеткого множества типа 2. Для FOU возможны многие другие формы.

FOU представляет собой размытие функции принадлежности типа 1 и полностью описывается двумя ее ограничивающими функциями (рис. 2), нижней функцией принадлежности (LMF) и верхней функцией принадлежности (UMF), обе из которых относятся к типу 1 нечеткие множества! Следовательно, можно использовать математику нечетких множеств типа 1 для описания и работы с интервальными нечеткими множествами типа 2. Это означает, что инженерам и ученым, которые уже знают нечеткие множества типа 1, не придется тратить много времени на изучение общей математики нечетких множеств типа 2, чтобы понять и использовать интервальные нечеткие множества типа 2.

Работа над нечеткими множествами типа 2 приостановилась в 1980-е и с начала до середины 1990-х годов, хотя о них было опубликовано небольшое количество статей. Люди все еще пытались выяснить, что делать с нечеткими множествами типа 1, поэтому, хотя Заде предложил нечеткие множества типа 2 в 1976 году, для исследователей было неподходящее время отказываться от того, что они делали с нечеткими множествами типа 1, чтобы сосредоточиться на нечетких множествах типа 2. Это изменилось во второй половине 1990-х годов в результате работ Джерри Менделя и его учеников по нечетким множествам и системам типа 2.[3] С тех пор все больше и больше исследователей во всем мире пишут статьи о нечетких множествах и системах типа 2.

Нечеткие множества с интервалом типа 2

Нечеткие множества с интервалом типа 2 привлекли наибольшее внимание, потому что математика, необходимая для таких множеств, в первую очередь Интервальная арифметика - намного проще, чем математика, необходимая для общих нечетких множеств типа 2. Итак, литературы об интервальных нечетких множествах типа 2 достаточно много, тогда как литературы об общих нечетких множествах типа 2 гораздо меньше. Оба вида нечетких множеств активно исследуются постоянно растущим числом исследователей по всему миру и привели к успешному применению в различных областях, таких как управление роботами.[4]

Для интервальных нечетких множеств типа 2 уже разработаны Formilleri для следующего:

  • Операции с нечеткими множествами: объединение, пересечение и дополнение[5][3]
  • Центроид (очень широко используемая практика таких наборов, а также важная мера неопределенности для них)[6][3][7]
  • Другие меры неопределенности [нечеткость, мощность, отклонение и перекос[8] и границы неопределенности[9]
  • Сходство[10][11][12]
  • Подмножество[13]
  • Встроенные нечеткие множества[14][15][16]
  • Рейтинг нечетких множеств[12]
  • Ранжирование и выбор нечетких правил[17]
  • Методы редукции типов[6][3]
  • Интервалы срабатывания системы нечеткой логики интервального типа 2[18][19][3]
  • Нечеткое средневзвешенное значение[20]
  • Лингвистическое средневзвешенное значение[21]
  • Синтез FOU из данных, собранных из группы субъектов[22]

Системы нечеткой логики с интервалом типа 2

Нечеткие множества типа 2 находят очень широкое применение в системах нечеткой логики (FLS), основанных на правилах, поскольку они позволяют моделировать неопределенности с их помощью, тогда как такие неопределенности не могут быть смоделированы нечеткими наборами типа 1. Блок-схема ДУТ типа 2 изображена на рис. 3. ДУТ такого типа используется в управлении нечеткой логикой, обработке сигналов нечеткой логики, классификации на основе правил и т. Д., И иногда его называют аппроксимация функции применение нечетких множеств, поскольку ДУТ призван минимизировать функцию ошибок.

Рис. 3. ДУТ типа 2

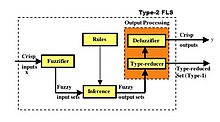
Следующие ниже обсуждения четырех компонентов на рис. 3 основанных на правилах ДУТ даны для интервального ДУТ 2 типа, поскольку на сегодняшний день они являются наиболее популярным типом ДУТ типа 2; тем не менее, большинство обсуждений применимо и к ДУТ второго типа.

Правила, которые либо предоставляются экспертами в данной области, либо извлечены из числовых данных, выражаются в виде набора операторов IF-THEN, например,

ЕСЛИ температура умеренный и давление высоко, затем поверните клапан немного правее.

Нечеткие множества связаны с терминами, которые появляются в антецедентах (IF-часть) или консеквентах (THEN-часть) правил, а также с входами и выходами FLS. Функции принадлежности используются для описания этих нечетких множеств, и в ДУТ типа 1 все они являются нечеткими множествами типа 1, тогда как в интервальном ДУТ типа 2 по крайней мере одна функция принадлежности является нечетким множеством интервала типа 2.

Интервальный ДУТ типа 2 позволяет количественно оценить один или все из следующих видов неопределенностей:

  1. Слова, которые используются в антецедентах и ​​следствиях правил, потому что слова могут означать разные вещи для разных людей.
  2. Неопределенные консеквенты - потому что, когда правила получены от группы экспертов, консеквенты часто будут разными для одного и того же правила, то есть эксперты не обязательно будут соглашаться.
  3. Параметры функции принадлежности - потому что, когда эти параметры оптимизируются с использованием неопределенных (зашумленных) обучающих данных, параметры становятся неопределенными.
  4. Шумные измерения - потому что очень часто именно такие измерения активируют ДУТ.

На рис. 3 измеренные (четкие) входные данные сначала преобразуются в нечеткие множества в Фаззификатор block, потому что это нечеткие множества, а не числа, которые активируют правила, описанные в терминах нечетких множеств, а не чисел. В интервальном ДУТ типа 2 возможны три типа фаззификаторов. Когда измерения бывают:

  • Идеально, они смоделированы как четкий набор;
  • Шумные, но шум стационарный, они моделируются нечетким множеством типа 1; и,
  • Шумные, но шум нестационарный, они моделируются как интервальное нечеткое множество типа 2 (этот последний вид фаззификации не может быть выполнен в ДУТ типа 1).

На рис. 3 после нечеткости измерений полученные входные нечеткие множества отображаются в нечеткие выходные наборы с помощью Вывод блокировать. Это достигается путем сначала количественной оценки каждого правила с использованием теории нечетких множеств, а затем использования математики нечетких множеств для установления результата каждого правила с помощью механизма вывода. Если есть M rules, то нечеткие входные наборы для блока вывода активируют только подмножество этих правил, где подмножество содержит по крайней мере одно правило и обычно намного меньше, чем M правила. Вывод делается по одному правилу за раз. Итак, на выходе блока Inference будет один или несколько нечеткие выходные наборы с установленным правилом.

В большинстве инженерных приложений ДУТ в качестве окончательного результата требуется число (а не нечеткое множество), например, следствием приведенного выше правила является «Поверните клапан немного вправо». Ни один автоматический клапан не узнает, что это означает, потому что «немного вправо» - это лингвистическое выражение, а клапан должен быть повернут на числовые значения, то есть на определенное количество градусов. Следовательно, выходные нечеткие множества сработавшего правила должны быть преобразованы в число, и это сделано на рис. Обработка вывода блокировать.

В ДУТ типа 1 обработка выходных данных называется "дефаззификация ", отображает нечеткое множество типа 1 в число. Есть много способов сделать это, например, вычислить объединение выходных нечетких наборов сработавшего правила (результат - еще один нечеткий набор типа 1), а затем вычислить центр силы тяжести функции принадлежности для этого набора; вычислить средневзвешенное значение центров тяжести каждой из последовательных функций принадлежности сработавшего правила и т. д.

Для интервального ДУТ типа 2 все несколько сложнее, потому что для перехода от нечеткого набора интервального типа 2 к числовому (обычно) требуется два шага (рис. 3). Первый шаг, называемый «редукцией типов», заключается в том, что интервальное нечеткое множество типа 2 сокращается до нечеткого множества типа 1 с интервалом. Существует столько же методов редукции типов, сколько существует методов дефаззификации типа 1. Алгоритм, разработанный Карником и Менделем[6][3] теперь известный как «алгоритм КМ» используется для редукции типов. Хотя этот алгоритм итеративный, он очень быстрый.

Второй этап обработки вывода, который происходит после редукции типов, по-прежнему называется «дефаззификацией». Поскольку приведенный к типу набор нечеткого множества интервального типа 2 всегда представляет собой конечный интервал чисел, дефаззифицированное значение является просто средним из двух конечных точек этого интервала.

Из рисунка 3 ясно, что может быть два выхода для интервального ДУТ 2-го типа - четкие числовые значения и набор с сокращенным типом. Последний обеспечивает меру неопределенностей, которые прошли через интервальный ДУТ типа 2, из-за (возможно) неопределенных входных измерений, которые активировали правила, антецеденты или следствия или и то и другое являются неопределенными. Подобно тому, как стандартное отклонение широко используется в вероятности и статистике для измерения непредсказуемой неопределенности относительно среднего значения, набор с уменьшенным типом может обеспечить меру неопределенности в отношении четких выходных данных интервального ДУТ 2 типа.

Вычисления со словами

Другое приложение для нечетких множеств также было вдохновлено Заде.[23][24][25] - «Вычисления со словами». Для слов «вычисления со словами» использовались разные акронимы, например CW и CWW. По словам Заде:

CWW - это методология, в которой объектами вычислений являются слова и предложения, взятые из естественного языка. [Он] вдохновлен замечательной способностью человека выполнять широкий спектр физических и умственных задач без каких-либо измерений и вычислений.

Конечно, он не имел в виду, что компьютеры на самом деле будут вычислять, используя слова - отдельные слова или фразы - а не числа. Он имел в виду, что компьютеры будут активироваться словами, которые будут преобразованы в математическое представление с использованием нечетких множеств, и что эти нечеткие множества будут отображены механизмом CWW в некоторый другой нечеткий набор, после чего последний будет преобразован обратно в слово. Возникает естественный вопрос: какой тип нечеткого набора - тип 1 или тип 2 - следует использовать в качестве модели для слова? Мендель[26][27] утверждал, на основании Карл Поппер концепция "фальсификационизм ",[28][25] что использование нечеткого множества типа 1 в качестве модели слова с научной точки зрения неверно. Нечеткое множество интервалов типа 2 следует использовать в качестве модели (неопределенности первого порядка) для слова. По CWW ведется много исследований.

Приложения

Нечеткие множества типа 2 применялись в следующих областях:

Программного обеспечения

Бесплатные реализации MATLAB, которые охватывают общие и интервальные нечеткие множества и системы типа 2, а также нечеткие системы типа 1, доступны по адресу: http://sipi.usc.edu/~mendel/software.
Программное обеспечение, поддерживающее дискретные интервальные системы нечеткой логики типа 2, доступно по адресу:
Набор инструментов DIT2FLS - http://dit2fls.com/projects/dit2fls-toolbox/
Пакет библиотеки DIT2FLS - http://dit2fls.com/projects/dit2fls-library-package/

Библиотеки Java, включая исходный код для нечетких систем типа 1, интервалов и общего типа 2, доступны по адресу: http://juzzy.wagnerweb.net/.

Библиотека Python для нечетких множеств типа 1 и типа 2 доступна по адресу: https://github.com/carmelgafa/type2fuzzy

Библиотека Python для нечетких множеств и систем интервального типа 2 доступна по адресу: https://github.com/Haghrah/PyIT2FLS

Набор инструментов Matlab / Simulink с открытым исходным кодом для систем нечеткой логики Interval Type-2 доступен по адресу: http://web.itu.edu.tr/kumbasart/type2fuzzy.htm

Смотрите также

Рекомендации

  1. ^ а б Л. А. Заде, "Понятие языковой переменной и ее применение к приближенному рассуждению – 1", Информационные науки, т. 8. С. 199–249, 1975.
  2. ^ Джерри Мендель; Хани Хаграс; Воэй-Ван Тан (16 июня 2014 г.). Введение в нечеткое логическое управление типа 2: теория и приложения. Вайли. ISBN  978-1-118-90144-1.
  3. ^ а б c d е ж Дж. М. Мендель, Нечеткие логические системы с неопределенными правилами: введение и новые направления, Прентис-Холл, Верхняя Седл-Ривер, Нью-Джерси, 2001.
  4. ^ Хасанзаде, Хамид Реза и др. «Интервальный нечеткий контроллер для сложных динамических систем с приложением к параллельному роботу 3-PSP». Нечеткие множества и системы 235 (2014): 83-100.
  5. ^ Карник Н. Н., Мендель Дж. М. Операции над нечеткими множествами типа 2. Нечеткие множества и системы, т. 122. С. 327–348, 2001.
  6. ^ а б c Карник Н. Н., Мендель Дж. М. Центроид нечеткого множества типа 2. Информационные науки, т. 132. С. 195–220, 2001.
  7. ^ О. Салазар, Дж. Сориано и Х. Серрано, «Краткое примечание о центроиде нечеткого множества интервального типа 2», в Proceedings of IEEE 2012 Workshop on Engineering Applications (WEA), Богота, Колумбия, май 2012 г., стр. 1–4
  8. ^ Д. Ву, Дж. М. Мендель, "Меры неопределенности для интервальных нечетких множеств типа 2", Информационные науки, т. 177, стр. 5378–5393, 2007.
  9. ^ Х. Ву и Дж. М. Мендель, "Границы неопределенности и их использование при проектировании интервальных систем нечеткой логики типа 2", IEEE Trans. по нечетким системам, т. 10. С. 622–639, октябрь 2002 г.
  10. ^ Х. Бустинс, "Индикатор степени включения для нечетких множеств с интервальными значениями: приложение для приближенного рассуждения на основе нечетких множеств с интервальными значениями", Международный журнал приблизительных рассуждений, т. 23. С. 137–209, 2000.
  11. ^ Д. Ву и Дж. М. Мендель, "Векторная мера подобия для интервальных нечетких множеств типа 2 и нечетких множеств типа 1", Информационные науки, т. 178. С. 381–402, 2008.
  12. ^ а б Д. Ву и Дж. М. Мендель, «Сравнительное исследование методов ранжирования, мер сходства и мер неопределенности для интервальных нечетких множеств типа 2», Информационные науки, чтобы появиться в 2009 году.
  13. ^ Дж. Т. Рикард, Дж. Эйсбетт, Дж. Гиббон ​​и Д. Моргенталер, «Нечеткое подмножество для нечетких множеств типа n», НАФИПС 2008, Документ № 60101, Нью-Йорк, май 2008 г.
  14. ^ О. Салазар и Дж. Сориано, «Генерация вложенных нечетких множеств типа 1 с помощью выпуклой комбинации», в материалах Ежегодного собрания NAFIPS Всемирного конгресса IFSA 2013 г., Эдмонтон, Канада, июнь 2013 г., стр. 51–56.
  15. ^ О. Салазар и Дж. Сориано, "Выпуклая комбинация и ее применение к нечетким множествам и интервальнозначным нечетким множествам I", Прикладные математические науки, т. 9, вып. 22. С. 1061–1068, 2015.
  16. ^ О. Салазар и Дж. Сориано, "Выпуклая комбинация и ее применение к нечетким множествам и интервальнозначным нечетким множествам II", Прикладные математические науки, т. 9, вып. 22. С. 1069–1076, 2015.
  17. ^ С. -М. Чжоу, Дж. М. Гарибальди, Р. И. Джон и Ф. Чиклана, «О построении экономных систем нечеткой логики типа 2 посредством выбора влиятельных правил», IEEE Trans. по нечетким системам, vol.17, no.3, pp. 654–667, 2009.
  18. ^ М. Б. Горзалчани, "Метод вывода в приближенном рассуждении, основанный на нечетких множествах с интервальными значениями", Нечеткие множества и системы, т. 21. С. 1–17, 1987.
  19. ^ К. Лян и Дж. М. Мендель, "Интервальные нечеткие логические системы типа 2: теория и дизайн", IEEE Trans. по нечетким системам, т. 8. С. 535–550, 2000.
  20. ^ Ф. Лю и Дж. М. Мендель, «Агрегация с использованием нечеткого взвешенного среднего, вычисленного с помощью алгоритмов КМ», IEEE Trans. по нечетким системам, т. 16, стр. 1–12, февраль 2008 г.
  21. ^ Д. Ву и Дж. М. Мендель, «Агрегация с использованием лингвистического взвешенного среднего и интервального нечетких множеств типа 2», IEEE Trans. по нечетким системам, т. 15. С. 1145–1161, декабрь 2007 г.
  22. ^ Ф. Лю и Дж. М. Мендель, «Кодирование слов в интервальные нечеткие множества типа 2 с использованием интервального подхода», IEEE Trans. по нечетким системам, т. 16, стр. 1503–1521, декабрь 2008 г.
  23. ^ Л. А. Заде, «Нечеткая логика = вычисления со словами», IEEE Trans. по нечетким системам, т. 4. С. 103–111, 1996.
  24. ^ Л. А. Заде, «От вычисления с числами к вычислению со словами - от манипулирования измерениями до манипуляции восприятием», IEEE Trans. по схемам и системам – 1, Фундаментальная теория и приложения, т. 4. С. 105–119, 1999.
  25. ^ а б Л. А. Заде, «К машинному интеллекту человеческого уровня - достижимо ли это? Необходимость смены новой парадигмы», Журнал IEEE Computational Intelligence Magazine, т. 3, стр. 11–22, август 2008 г.
  26. ^ Дж. М. Мендель, «Нечеткие множества слов: новое начало», Proc. Конференция IEEE FUZZ, Сент-Луис, Миссури, 26–28 мая 2003 г., стр. 37–42.
  27. ^ Дж. М. Мендель, "Вычисления со словами: Заде, Тьюринг, Поппер и Оккам", Журнал IEEE Computational Intelligence Magazine, т. 2, с. 10–17, ноябрь 2007 г.
  28. ^ К. Поппер, Логика научных открытий (перевод Logik der Forschung), Хатчинсон, Лондон, 1959.
  29. ^ Кастильо, Оскар и др. «Обзор последних приложений для обработки нечетких изображений типа 2». Информация 8.3 (2017): 97.
  30. ^ Zarandi, MH Fazel, et al. «Разработка общей нечеткой экспертной системы 2-го типа для диагностики депрессии». Прикладные мягкие вычисления 80 (2019): 329-341.
  31. ^ Дирик, Махмут, Оскар Кастильо и Аднан Фатих Кодамаз. «Глобальное планирование пути на основе визуального сервоуправления с использованием интервального управления нечеткой логикой типа 2». Аксиомы 8.2 (2019): 58.
  32. ^ Мо, Хун, Сюаньмин Чжао и Фей-Юэ Ван. «Применение интервальных нечетких множеств типа 2 в визуальном наведении беспилотных транспортных средств». Международный журнал нечетких систем 21.6 (2019): 1661-1668.
  33. ^ Chai K.C .; Тай К. М .; Lim C.P. (2016). «Основанный на перцепционных вычислениях метод определения приоритетов режимов отказа в режиме отказа и анализа последствий и его применение в выращивании съедобных птичьих гнезд» (PDF). Прикладные мягкие вычисления. 49: 734–747. Дои:10.1016 / j.asoc.2016.08.043.
  34. ^ Дарбан, Захра Заманзаде и Мохаммад Хади Валипур. «Интервальная локально-линейная нейро-нечеткая модель 2-го типа на основе локально-линейного модельного дерева». Международная конференция по искусственному интеллекту и мягким вычислениям. Спрингер, Чам, 2015.
  35. ^ Биби, Юсуф, Омар Бухали и Тарек Буктир. «Аппроксиматор нечетких нейронных сетей Петри типа 2 для адаптивного управления неопределенными нелинейными системами». IET Control Theory & Applications 11.17 (2017): 3130-3136.
  36. ^ Тай, Кевин и др. «Обзор последних приложений нечетких контроллеров типа 2». Алгоритмы 9.2 (2016): 39.

внешняя ссылка

Есть два Эксперт IEEE сейчас мультимедийные модули, к которым можно получить доступ из IEEE по адресу: http://www.ieee.org/web/education/Expert_Now_IEEE/Catalog/AI.html

  • "Введение в нечеткие множества и системы типа 2" Джерри Менделя, спонсируемое Обществом вычислительного интеллекта IEEE
  • "Контроллеры с нечеткой логикой типа 2: на пути к новому подходу к управлению неопределенностями в реальных средах" Хани Хаграс, спонсор IEEE Computational Intelligence Society