Амплитудная манипуляция - Amplitude-shift keying

Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: эта статья нуждается в нейтральной и лучшей формулировке Пожалуйста помоги улучшить эту статью если вы можете. (Ноябрь 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Амплитудная манипуляция (ПРОСИТЬ) является формой амплитудная модуляция что представляет цифровые данные как вариации в амплитуда из несущая волна.В системе ASK двоичный символ с d-амплитудой несущей и фиксированной частотой для длительности битов T секунд. Если значение сигнала равно 1, то будет передаваться несущий сигнал; в противном случае будет передано значение сигнала 0.

Любая схема цифровой модуляции использует конечный количество различных сигналов для представления цифровых данных. ASK использует конечное количество амплитуд, каждой из которых назначен уникальный образец двоичные цифры. Обычно каждая амплитуда кодирует равное количество битов. Каждая комбинация битов образует символ что представлено определенной амплитудой. В демодулятор, который разработан специально для набора символов, используемого модулятором, определяет амплитуду принятого сигнала и отображает ее обратно в символ, который он представляет, таким образом восстанавливая исходные данные. Частота и фаза перевозчика остаются постоянными.

Нравиться ЯВЛЯЮСЬ, ASK также линейен и чувствителен к атмосферному шуму, искажениям, условиям распространения на разных маршрутах в PSTN и т. д. Процессы модуляции ASK и демодуляции относительно недороги. Метод ASK также обычно используется для передачи цифровые данные по оптическому волокну. Для светодиодных передатчиков двоичная 1 представлена ​​коротким световым импульсом, а двоичная 0 - отсутствием света. Лазерные передатчики обычно имеют фиксированный ток «смещения», который заставляет устройство излучать слабый уровень света. Этот низкий уровень представляет двоичный 0, в то время как световая волна с более высокой амплитудой представляет двоичную 1.

Самая простая и наиболее распространенная форма ASK работает как переключатель, используя наличие несущей волны для обозначения двоичной единицы и ее отсутствие для обозначения двоичного нуля. Этот вид модуляции называется включение-выключение (OOK) и используется на радиочастотах для передачи кода Морзе (так называемый режим непрерывной волны),

Были разработаны более сложные схемы кодирования, которые представляют данные в группах с использованием дополнительных уровней амплитуды. Например, четырехуровневая схема кодирования может представлять два бита с каждым сдвигом по амплитуде; восьмиуровневая схема может представлять три бита; и так далее. Эти формы амплитудной манипуляции требуют высокого отношения сигнал / шум для их восстановления, поскольку по их природе большая часть сигнала передается с пониженной мощностью.

Диаграмма ASK

Систему ASK можно разделить на три блока. Первый представляет передатчик, второй - линейную модель эффектов канала, третий - структуру приемника. Используются следующие обозначения:

• час_т(f) - несущий сигнал для передачи
• час_c(е) - импульсная характеристика канала
• п(t) - шум, вносимый каналом
• час_р(f) - фильтр на приемнике
• L это количество уровней, которые используются для передачи
• Т_s это время между генерацией двух символов

Различные символы представлены с разными напряжениями. Если максимально допустимое значение напряжения равно A, тогда все возможные значения находятся в диапазоне [-A, A], и они определяются как:

${ displaystyle v_ {i} = { frac {2A} {L-1}} i-A; quad i = 0,1, dots, L-1}$

разница между одним напряжением и другим составляет:

${ displaystyle Delta = { frac {2A} {L-1}}}$

Рассматривая изображение, символы v [n] генерируются случайным образом источником S, затем генератор импульсов создает импульсы с площадью v [n]. Эти импульсы отправляются на фильтр ht для передачи по каналу. Другими словами, для каждого символа передается отдельная несущая волна с относительной амплитудой.

Вне передатчика сигнал s (t) можно выразить в виде:

${ displaystyle s (t) = sum _ {n = - infty} ^ { infty} v [n] cdot h_ {t} (t-nT_ {s})}$

В приемнике после фильтрации через hr (t) сигнал:

${ displaystyle z (t) = n_ {r} (t) + sum _ {n = - infty} ^ { infty} v [n] cdot g (t-nT_ {s})}$

где мы используем обозначения:

${ Displaystyle { begin {align} n_ {r} (t) & = n (t) * h_ {r} (t) g (t) & = h_ {t} (t) * h_ {c} (т) * ч_ {г} (т) конец {выровнено}}}$

где * указывает свертку между двумя сигналами. После аналого-цифрового преобразования сигнал z [k] можно выразить в виде:

${ Displaystyle г [к] = п_ {г} [к] + v [к] г [0] + сумма _ {п neq k} v [п] г [к-п]}$

В этой связи второй член представляет извлекаемый символ. Остальные нежелательны: первый - эффект шума, третий - межсимвольные помехи.

Если фильтры выбраны так, что g (t) удовлетворяет критерию ISI Найквиста, то межсимвольной интерференции не будет и значение суммы будет равно нулю, поэтому:

${ Displaystyle г [к] = п_ {г} [к] + v [к] г [0]}$

на передачу будет влиять только шум.

Вероятность ошибки

Функция плотности вероятности наличия ошибки заданного размера может быть смоделирована функцией Гаусса; среднее значение будет относительным отправленным значением, а его отклонение будет выражаться следующим образом:

${ displaystyle sigma _ {N} ^ {2} = int _ {- infty} ^ {+ infty} Phi _ {N} (f) cdot | H_ {r} (f) | ^ { 2} df}$

куда ${ Displaystyle Phi _ {N} (е)}$ - спектральная плотность шума внутри полосы, а Hr (f) - непрерывное преобразование Фурье импульсной характеристики фильтра hr (f).

Вероятность ошибки определяется по формуле:

${ displaystyle P_ {e} = P_ {e | H_ {0}} cdot P_ {H_ {0}} + P_ {e | H_ {1}} cdot P_ {H_ {1}} + cdots + P_ {e | H_ {L-1}} cdot P_ {H_ {L-1}} = sum _ {k = 0} ^ {L-1} P_ {e | H_ {k}} cdot P_ {H_ {k}}}$

где, например, ${ displaystyle P_ {e | H_ {0}}}$ это условная вероятность ошибки при условии, что символ v0 был отправлен и ${ displaystyle P_ {H_ {0}}}$ - вероятность отправки символа v0.

Если вероятность отправки любого символа одинакова, то:

${ displaystyle P_ {H_ {i}} = { frac {1} {L}}}$

Если мы представим все функции плотности вероятности на одном графике в зависимости от возможного значения передаваемого напряжения, мы получим такую ​​картину (частный случай ${ displaystyle L = 4}$ Показано):

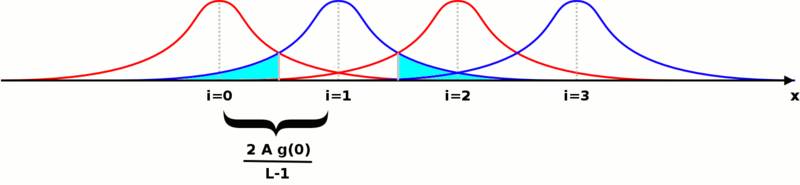
Вероятность ошибки после отправки одного символа - это область функции Гаусса, подпадающая под функции для других символов. Только для одного из них он отображается голубым цветом. Если мы позвоним ${ Displaystyle P ^ {+}}$ площадь под одной стороной гауссиана, сумма всех площадей будет: ${ displaystyle 2LP ^ {+} - 2P ^ {+}}$. Полная вероятность совершения ошибки может быть выражена в виде:

${ displaystyle P_ {e} = 2 left (1 - { frac {1} {L}} right) P ^ {+}}$

Теперь нам нужно вычислить значение ${ Displaystyle P ^ {+}}$. Для этого мы можем переместить исходную точку ссылки в любое место: область под функцией не изменится. Мы находимся в ситуации, подобной показанной на следующем рисунке:

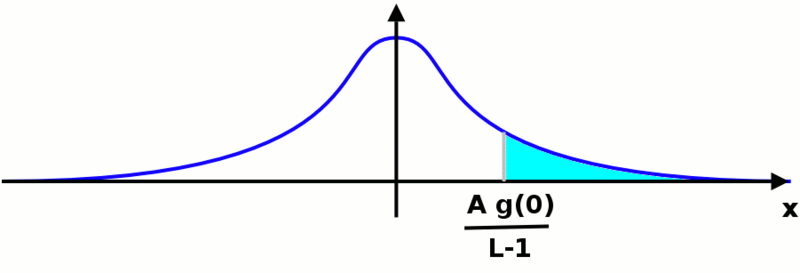
не имеет значения, какую функцию Гаусса мы рассматриваем, площадь, которую мы хотим вычислить, будет такой же. Искомое значение будет дано следующим интегралом:

${ Displaystyle P ^ {+} = int _ { frac {Ag (0)} {L-1}} ^ { infty} { frac {1} {{ sqrt {2 pi}} sigma _ {N}}} e ^ {- { frac {x ^ {2}} {2 sigma _ {N} ^ {2}}}} dx = { frac {1} {2}} operatorname { erfc} left ({ frac {Ag (0)} {{ sqrt {2}} (L-1) sigma _ {N}}} right)}$

куда ${ displaystyle operatorname {erfc} (x)}$ - дополнительная функция ошибок. Сложив все эти результаты вместе, вероятность ошибки составляет:

${ displaystyle P_ {e} = left (1 - { frac {1} {L}} right) operatorname {erfc} left ({ frac {Ag (0)} {{ sqrt {2}) } (L-1) sigma _ {N}}} right)}$

из этой формулы легко понять, что вероятность ошибки уменьшается, если максимальная амплитуда передаваемого сигнала или усиление системы становится больше; с другой стороны, он увеличивается, если количество уровней или мощность шума становится больше.

Это соотношение справедливо, когда нет межсимвольной интерференции, т.е. ${ displaystyle g (t)}$ это Функция Найквиста.

Смотрите также

• Частотная манипуляция (ФСК)

внешняя ссылка

• Расчет чувствительности приемника с амплитудной манипуляцией (ASK)