Дельта-сигма модуляция - Delta-sigma modulation
Дельта-сигма (ΔΣ; или же сигма-дельта, ΣΔ) модуляция - это метод кодирования аналоговые сигналы в цифровые сигналы как найдено в аналого-цифровой преобразователь (АЦП). Он также используется для преобразования низкочастотных цифровых сигналов с большим числом битов в цифровые сигналы с более низким числом битов и более высокой частотой как часть процесса преобразования цифровых сигналов в аналоговые как часть цифро-аналоговый преобразователь (ЦАП).
В обычном АЦП аналоговый сигнал отобранный с частотой дискретизации и впоследствии квантованный в многоуровневом квантователе в цифровой сигнал. Этот процесс вносит шум ошибки квантования. Первый шаг в дельта-сигма-модуляции - это дельта-модуляция. В дельта-модуляция кодируется изменение сигнала (его дельта), а не абсолютное значение. В результате получается поток импульсов, а не поток чисел, как в случае с импульсная кодовая модуляция (PCM). При дельта-сигма-модуляции точность модуляции повышается путем пропускания цифрового выхода через 1-битный ЦАП и добавления (сигма) результирующего аналогового сигнала к входному сигналу (сигнал до дельта-модуляции), тем самым уменьшая ошибку, вносимую дельта-модуляция.
И АЦП, и ЦАП могут использовать дельта-сигма модуляцию. Дельта-сигма АЦП сначала кодирует аналоговый сигнал, используя высокочастотную дельта-сигма модуляцию, а затем применяет цифровой фильтр для формирования цифрового выходного сигнала с более высоким разрешением, но с более низкой частотой дискретизации. Дельта-сигма ЦАП кодирует цифровой входной сигнал высокого разрешения в сигнал с более низким разрешением, но с более высокой частотой дискретизации, который отображается на напряжения, а затем сглаживается аналоговым фильтром. В обоих случаях временное использование сигнала с более низким разрешением упрощает конструкцию схемы и повышает эффективность.
В первую очередь из-за его экономической эффективности и меньшей сложности схемы, этот метод нашел все более широкое применение в современных электронных компонентах, таких как ЦАП, АЦП, синтезаторы частот, импульсные источники питания и контроллеры двигателей.[1] Грубо-квантованный выход дельта-сигма-модулятора иногда используется непосредственно при обработке сигналов или как представление для хранения сигнала. Например, Супер аудио компакт-диск (SACD) сохраняет выходной сигнал дельта-сигма-модулятора непосредственно на диске.
Мотивация
Дельта-сигма модуляция преобразует аналоговый сигнал напряжения в частоту импульсов или плотность импульсов, которую можно понимать как модуляция плотности импульса (ДПМ). Последовательность положительных и отрицательных импульсов, представляющих биты с известной фиксированной скоростью, очень легко сгенерировать, передать и точно регенерировать в приемнике, если только можно восстановить синхронизацию и знак импульсов. Учитывая такую последовательность импульсов от дельта-сигма модулятора, исходная форма волны может быть восстановлена с достаточной точностью. Напротив, без преобразования в поток импульсов, а просто передачи аналогового сигнала напрямую, все шум в системе будет добавлен аналоговый сигнал, что снизит его качество. Использование PDM в качестве представления сигнала является альтернативой импульсно-кодовая модуляция (PCM), выборка и квантование в многобитовый код на Курс Найквиста.
Аналого-цифровое преобразование
Описание
Дельта-сигма или другой модулятор плотности или частоты импульсов генерирует поток импульсов, в котором частота, ж, импульсов в потоке пропорционально входному аналоговому напряжению, v, так что ж = k · v, куда k является константой для конкретной реализации. Контур обратной связи контролирует интеграл v и когда этот интеграл увеличился на Δ, на что указывает пересечение интегральной формы сигнала порога, Т, это вычитает Δ из интеграла v так что комбинированные пилообразные формы волны между Т и Т - Δ. На каждом шаге к потоку импульсов добавляется импульс.
Счетчик суммирует количество импульсов, которые происходят в заранее определенный период, так что сумма, , является . В данной реализации выбирается таким образом, чтобы цифровое отображение счета, , это отображение с заданным коэффициентом масштабирования. Потому что может принимать любое расчетное значение, оно может быть достаточно большим, чтобы обеспечить любое желаемое разрешение или точность.
Анализ
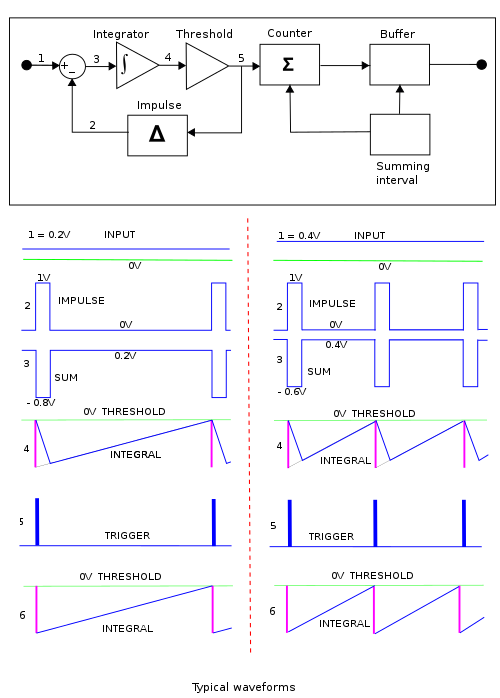

В целях введения на рисунке 1 показана концепция преобразования напряжения в частоту в несинхронизированной форме, которая напоминает дельта-сигма модуляцию и называется асинхронная модуляция,[2] асинхронная дельта-сигма модуляция,[3][4] или же автономные модуляторы.[5]
Ниже показаны формы сигналов в точках, обозначенных цифрами от 1 до 5, для входного напряжения 0,2 В в левом столбце и 0,4 В в правом столбце. Поток дельта-импульсов, генерируемых при каждом пересечении порога, показан в (2), а разница между (1) и (2) показана в (3). Эта разница интегрированный для создания сигнала (4). Детектор порога генерирует импульс (5), который начинается, когда форма волны (4) пересекает порог, и сохраняется до тех пор, пока форма волны (4) не упадет ниже порога. Порог (5) запускает генератор импульсов для создания импульса фиксированной силы.
Интеграл (4) в правом столбце пересекает порог вдвое быстрее, чем в левом столбце. Таким образом частота импульсов увеличивается вдвое. Следовательно, счетчик увеличивается в два раза быстрее, чем справа; это удвоение частоты следования импульсов соответствует удвоению входного напряжения.
Построению форм сигналов, показанных в (4), помогают концепции, связанные с Дельта-функция Дирака в том, что по определению все импульсы одинаковой силы производят один и тот же шаг при объединении. Затем (4) строится с использованием промежуточного шага (6), гипотетическая форма волны не в схеме, а в которой каждый интегрированный импульс идеальной дельта-функции интегрируется с шагом. Эффект конечной длительности фактического импульса построен в (4) путем проведения линии от основания импульсной ступени при нулевом напряжении до пересечения с линией затухания из (6) при полной длительности импульса.
В схеме за пределами цикла интервал суммирования - это заранее заданное фиксированное время, и по его истечении счет сохраняется, а буфер и счетчик сбрасываются. Затем буфер представляет последовательность цифровых значений, соответствующих квантованиям уровней аналогового сигнала в течение интервалов суммирования. Использование интервала суммирования - это способ (не обязательно идеальный способ) квантовать поток асинхронных импульсов в код; он будет иметь меньше ошибок квантования, если начало интервала синхронизировано с импульсом.
Преобразователи дельта-сигма дополнительно ограничивают работу генератора импульсов, так что начало импульса задерживается до следующего появления соответствующей границы тактового импульса. Эффект этой задержки показан на рисунке 1a для последовательности импульсов, которые возникают с номинальными интервалами 2,5 такта.
Практическая реализация


Принципиальная схема реализации дельта-сигма модулятора показана на рисунке 1b, а соответствующие формы сигналов - на рисунке 1c. Формы сигналов, показанные на Рисунке 1c, необычно сложны, потому что они предназначены для иллюстрации поведения контура в экстремальных условиях. Vв насыщенный при полной шкале 1,0 В и насыщенный при нуле. Также указывается промежуточное состояние, Vв при 0,4 В, что очень похоже на работу, показанную на Рисунке 1.
В верхней части рисунка 1c показаны формы сигналов, обозначенные так, как они есть на принципиальной схеме:
- Часы
- (а) Vв - это показано как изменяющееся от 0,4 В вначале до 1,0 В, а затем до нуля вольт, чтобы показать влияние на контур обратной связи.
- (б) Форма импульса, подаваемого на интегратор. Контролируется резкий поворот результат (f) ниже.
- (c) Ток в конденсаторе, яc, Является линейной суммой импульсов опорного напряжения разделены р и Vв деленное на р. Чтобы показать эту сумму в виде напряжения, произведение р × яc нанесен. Входной импеданс усилителя считается настолько высоким, что ток, потребляемый входом, не учитывается. Конденсатор подключается между отрицательной входной клеммой усилителя и его выходной клеммой. При таком подключении он обеспечивает отрицательную обратную связь вокруг усилителя. Изменение входного напряжения равно изменению выходного напряжения, деленному на коэффициент усиления усилителя. При очень высоком усилении усилителя изменением входного напряжения можно пренебречь, и поэтому входное напряжение поддерживается близким к напряжению на положительной входной клемме, которое в этом случае поддерживается на уровне 0 В. Поскольку напряжение на входной клемме равно 0 В, напряжение на р просто Vв так что ток в конденсаторе равен входному напряжению, деленному на сопротивление р.
- (d) Отрицательный интеграл от яc. Это отрицание стандартно для интегратор операционного усилителя и возникает потому, что ток в конденсаторе на входе усилителя - это ток из конденсатора на выходе усилителя, а напряжение является интегралом тока, деленного на емкость C.
- (e) Выход компаратора. Компаратор очень высокий усилитель усиления с его входным выводом подключенного для справки до 0,0 В. Каждый раз, когда отрицательный входной терминал принимается отрицательным по отношению к положительной клемме усилителя выходных насыщается положительно и, наоборот, отрицательное насыщение для положительного входа. Таким образом, выходные насыщается положительным всякий раз, когда интеграл (г) опускается ниже исходного уровня 0 В, а на выходе остается там до (г) идет положительным по отношению к опорному 0 V.
- (f) Импульсный таймер срабатывает по положительному фронту D-типа. резкий поворот. Входная информация, подаваемая в D, передается в Q при появлении положительного фронта тактового импульса. Таким образом, когда выход компаратора (e) положительный, Q становится положительным или остается положительным на следующем положительном фронте тактового сигнала. Точно так же, когда (e) отрицательно, Q становится отрицательным на следующем положительном фронте тактового сигнала. Q управляет электронным переключателем, чтобы генерировать импульс тока (b) в интеграторе. Исследование формы сигнала (e) в течение начального периода, показанного, когда Vв составляет 0,4 В, показывает (e) пересечение порога задолго до положительного фронта тактового импульса, так что есть заметная задержка перед началом импульса. После начала импульса происходит дальнейшая задержка, пока (d) поднимается обратно за порог. В течение этого времени выход компаратора (e) остается высоким, но становится низким перед следующим фронтом триггера, в этот момент импульсный таймер переходит в низкий уровень, чтобы следовать за компаратором. Таким образом, часы частично определяют продолжительность импульса. Для следующего импульса порог пересекает непосредственно перед фронтом триггера, поэтому компаратор лишь кратковременно дает положительный результат. Vв (а) затем переходит в полную шкалу, +Vссылка, незадолго до окончания следующего импульса. В течение оставшейся части этого импульса ток конденсатора (c) стремится к нулю и, следовательно, крутизна интегратора на короткое время стремится к нулю. После этого импульса протекает полномасштабный положительный ток (c), и интегратор опускается с максимальной скоростью и, таким образом, пересекает порог задолго до следующего фронта запуска. На этом краю начинается импульс и Vв ток теперь согласован с эталонным током, так что чистый ток конденсатора (c) равен нулю. Теперь интеграция имеет нулевой наклон и остается на отрицательном значении, которое было в начале импульса. Это приводит к тому, что импульсный ток остается включенным, потому что Q остается положительным, потому что компаратор остается положительным на каждом фронте запуска. Это согласуется с непрерывными, стыковочными импульсами, которые характерны для входного сигнала полной шкалы. Следующий Vв (a) стремится к нулю, что приводит к тому, что текущая сумма (c) становится полностью отрицательной, а интеграл нарастает. Вскоре после этого он пересекает порог, после чего следует Q, таким образом отключая импульсный ток. Конденсаторный ток (c) теперь равен нулю, поэтому интегральный наклон равен нулю, оставаясь постоянным на значении, которое он приобрел в конце импульса.
- (g) Счетный поток генерируется путем стробирования инвертированных часов с помощью Q для создания этой формы сигнала. После этого интервал суммирования, количество сигм и количество в буфере производятся с использованием соответствующих счетчиков и регистров.
Улучшения разрешения и шума
Изучение рисунка 1c (g) показывает, что в потоке счета есть нулевые импульсы, когда входное напряжение равно нулю. Это условие может привести к тому, что высокочастотные компоненты сложного сигнала не будут разрешены. Этот эффект известен как интермодуляционные искажения (IMD). Одна из ловушек применения линейного анализа к нелинейной системе заключается в том, что IMD, поскольку это может быть следствием нелинейности, не присутствует в анализе. Чисто в иллюстративных целях способ смягчить это - добавить постоянное смещение 0,5 В к входному напряжению, чтобы оно теперь могло колебаться на +/- 0,5 В относительно смещения. Теперь это имеет нулевые импульсы в счетном потоке, когда входной сигнал -0,5 В. Затем мы должны ограничить размах входного сигнала до +/- 0,4 В, скажем, так, чтобы минимальная частота счетного потока была больше нуля. Мы можем выбрать тактовую частоту так, чтобы минимальная частота счетного потока при -0,4 В была намного больше, чем Курс Найквиста, так что разрешается даже самая высокая входная частотная составляющая. Мы можем увеличить тактовую частоту еще выше, пока фильтр нижних частот в достаточной степени устраняет пульсации, полностью восстанавливая входной сигнал. В этом иллюстративном обсуждении отфильтрованный сигнал также восстановит смещение, которое может быть устранено аналоговым сумматором, при этом сохраняя постоянную составляющую входного сигнала.
Замечания
По словам Вули,[6] Основополагающая статья, объединяющая обратную связь с передискретизацией для достижения дельта-модуляции, была написана Ф. де Ягером в 1952 году.[7]
Конфигурация дельта-сигма была разработана Inose et al. в 1962 г. для решения задач точной передачи аналоговых сигналов.[8] В этом приложении был передан поток импульсов, а исходный аналоговый сигнал восстановлен с помощью фильтра нижних частот после преобразования полученных импульсов. Этот фильтр нижних частот выполнял функцию суммирования, связанную с Σ. Они представили высокоматематический подход к ошибкам передачи, применимый к потоку импульсов, но эти ошибки теряются в процессе накопления, связанном с Σ.
Для аналогового к применению цифрового преобразования каждому импульс в потоке счета является образцом среднего значения входного напряжения равным опорного напряжения разделить интервал между импульсами, Ts. Это потому, что это интеграция формы входного сигнала по интервалу ts. Частотный диапазон Анализ сложной формы волны в этом интервале ts будет представлять ее как сумму константы, основной гармоники и гармоник, каждая из которых имеет точное целое число циклов по ts. Интеграл синусоидальной волны за один или несколько полных циклов равен нулю. Следовательно, интеграл входящей формы волны за интервал ts сводится к среднему значению за интервал. Подсчет N, накопленный в течение интервала суммирования, представляет N выборок среднего значения, а N, разделенное на счет, определяющий интервал суммирования, таким образом, является средним значением и поэтому подвержен небольшому отклонению.
Цифро-аналоговое преобразование
Как правило, ЦАП преобразует цифровое число N, представляющее некоторое аналоговое значение, в это аналоговое значение напряжения. Для преобразования цифровое число сначала загружается в счетчик. Затем счетчик ведет обратный отсчет до нуля с последовательностью импульсов, равным N. Каждому импульсу строки дается известный интеграл δ. Затем струна интегрируется, чтобы получить N.δ, сумму импульсов. Это необходимое аналоговое напряжение.
В некоторых приложениях, где аналоговый сигнал представлен серией цифровых чисел, которые требуют преобразования в частотно-модулированный поток, может быть достаточно взять поток импульсов (двух или трехуровневый), полученный в результате преобразования ЦАП каждого числа N по очереди. и применить этот поток через фильтр нижних частот непосредственно к выходу. Выходной сигнал перед фильтрацией будет грубо модулированным по частоте потоком с пакетами импульсов, пропорциональными по длине и количеству аналогу N, разделенных пустыми интервалами между пакетами.
Чтобы удалить пустые интервалы и улучшить шумовые характеристики, полное преобразование в аналоговое напряжение каждого последующего N с помощью ЦАП, описанного выше, может проводиться в образец и держать Затем схема передается в дельта-сигма-преобразователь для создания потока непрерывных пакетов, частота каждого из которых пропорциональна его генерирующему N.
Структуры децимации
Концептуально простейшая структура прореживания - это счетчик, который сбрасывается в ноль в начале каждого периода интегрирования, а затем считывается в конце периода интегрирования.
Многоступенчатое формирование шума (МАШ)[9] структура имеет формирование шума свойство, и обычно используется в цифровых звуковых синтезаторах и синтезаторах частот с дробным N. Он состоит из двух или более каскадных переполненных аккумуляторов, каждый из которых эквивалентен сигма-дельта-модуляторам первого порядка. Выходы переноса объединяются посредством суммирования и задержек для получения двоичного выхода, ширина которого зависит от количества каскадов (порядка) MASH. Помимо функции формирования шума, он имеет еще два привлекательных свойства:
- проста в аппаратной реализации; только общие цифровые блоки, такие как аккумуляторы, сумматоры, и Шлепанцы D необходимы
- безусловно устойчива (за пределами аккумуляторов отсутствуют петли обратной связи)
Очень популярная структура прореживания - это грех фильтр. Для модуляторов второго порядка sinc3 фильтр близок к оптимальному.[10][11]
Пример децимации
Давайте, например, имеем децимационный фильтр 8: 1 и 1-битовый поток битов; если у нас есть входной поток, например 10010110, подсчитав количество единиц, мы получим 4. Тогда результат прореживания будет 4/8 = 0,5. Затем мы можем представить его 3-битным числом 100 (двоичное), что означает половину максимально возможного числа. Другими словами,
- частота дискретизации уменьшается в восемь раз
- последовательная (1-битная) входная шина становится параллельной (3-битной) выходной шиной.
После применения прореживания и передачи n-битных кодов сигнал становится импульсная кодовая модуляция. Прореживание сильно связано с дельта-сигма-модуляцией, но необходимо проводить различие.
Вариации
Существует множество видов АЦП, которые используют эту дельта-сигма-структуру. Вышеупомянутый анализ сосредоточен на простейшем двухуровневом сигма-дельта-АЦП с равномерным прореживанием 1-го порядка. Многие АЦП используют 5-уровневый сигма-сигнал sinc3 второго порядка. дельта-структура. Во многом из того, что далее следует, используются загадочные сокращения с использованием символов, представляющих операционные функции с анализом в терминах преобразований Лапласа и т. Д. Это общепринятый язык индустрии передачи данных, и он не распространяется на широкую публику. Если требуется более полная документация по конкретному методу, не ищите ничего, кроме патентов. (Патентные эксперты обычно требуют полного раскрытия информации.) Прекрасная история - это «Эволюция аналого-цифровых преобразователей с передискретизацией» Брюса А. Вули, в которой содержится много ссылок на соответствующие патенты.
Модулятор второго и высшего порядка
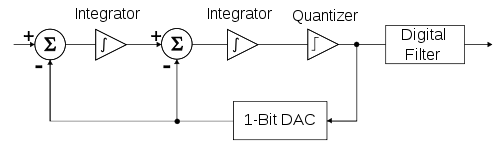
Количество интеграторов, а следовательно, и количество контуров обратной связи указывает на порядок модулятора ΔΣ; ΔΣ-модулятор второго порядка показан на рисунке 4. Модуляторы первого порядка безусловно стабильны, но для модуляторов более высокого порядка необходимо проводить анализ устойчивости.
Трехуровневый квантователь и выше
Модулятор также можно классифицировать по количеству битов, которые он имеет на выходе, что строго зависит от выхода квантователя. Квантователь может быть реализован с N-уровень компаратор, таким образом, модулятор имеет бревно2N-битовый выход. Простой компаратор имеет 2 уровня, как и 1-битный квантователь; трехуровневый квантователь называется «1,5-битным квантователем»; 4-уровневый квантователь - это 2-битный квантователь; 5-уровневый квантователь называется «2,5-битным» квантователем.[12]
Связь с дельта-модуляцией
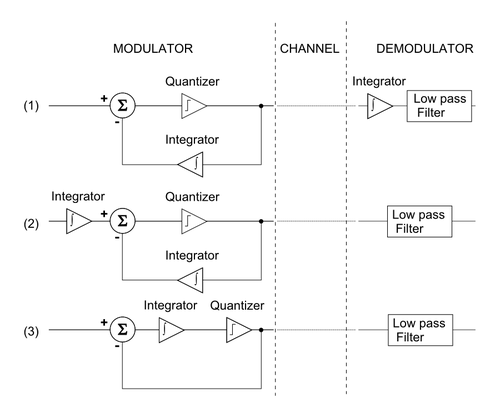

Модуляция дельта-сигма вдохновлена дельта-модуляция, как показано на рисунке 2. Если квантование мы однородный (например, если бы это было линейный ), следующее было бы достаточным выводом эквивалентности:
- Начните с блок-схемы дельта-модулятора / демодулятора.
- Свойство линейности интегрирования, , позволяет перемещать интегратор, восстанавливающий аналоговый сигнал в секции демодулятора, перед дельта-модулятором.
- Опять же, свойство линейности интегрирования позволяет объединить два интегратора и получить блок-схему дельта-сигма-модулятора / демодулятора.
Поскольку квантователь нет однородный, дельта-сигма вдохновленный с помощью дельта-модуляции, но они работают по-разному.
Из первой блок-схемы на рисунке 2 интегратор в тракте обратной связи может быть удален, если обратная связь берется непосредственно со входа фильтра нижних частот. Следовательно, для дельта-модуляции входного сигнала ты, фильтр нижних частот видит сигнал
Однако сигма-дельта-модуляция одного и того же входного сигнала влияет на фильтр нижних частот.
Другими словами, дельта-сигма и дельта-модуляция меняют местами интегратор и квантователь. Итоговым эффектом является более простая реализация, которая имеет дополнительное преимущество, заключающееся в формировании шума квантования вдали от сигналов, представляющих интерес (т. Е. Представляющие интерес сигналы фильтруются по нижним частотам, а шум квантования фильтруется по верхним частотам). Этот эффект становится более драматичным с увеличением передискретизация, что позволяет отчасти программировать шум квантования. С другой стороны, дельта-модуляция одинаково формирует и шум, и сигнал.
Кроме того, квантователь (например, компаратор ), используемый в дельта-модуляции, имеет небольшой выход, представляющий небольшой шаг вверх и вниз квантованного приближения входа, в то время как квантователь, используемый в дельта-сигма, должен принимать значения за пределами диапазона входного сигнала, как показано на рисунке 3.
В целом, дельта-сигма имеет некоторые преимущества по сравнению с дельта-модуляцией:
- Структура упрощена как
- нужен только один интегратор,
- демодулятор может быть простым линейным фильтром (например, RC- или LC-фильтром) для восстановления сигнала и
- квантователь (например, компаратор) может иметь полноразмерные выходы
- Квантованное значение представляет собой интеграл разностного сигнала, что делает его менее чувствительным к скорости изменения сигнала.
Формулы теории квантования
Когда сигнал квантуется, результирующий сигнал имеет статистику приблизительно второго порядка сигнала с добавленным независимым белым шумом. Предполагая, что значение сигнала находится в диапазоне одного шага квантованного значения с равным распределением, среднеквадратичное значение этого шума квантования равно
В действительности шум квантования, конечно, не зависит от сигнала, и эта зависимость приводит к предельные циклы и является источником холостых тонов и структурного шума в сигма-дельта преобразователях.
Шум квантования можно уменьшить, увеличив коэффициент передискретизации (OSR), определяемый
куда частота дискретизации и является Курс Найквиста.
В RMS шумовое напряжение в интересующей полосе () можно выразить через OSR
- [нужна цитата ]
Передискретизация

ΔΣ-модуляция - это метод передискретизация для уменьшения шума в интересующей полосе частот (зеленый на рисунке 5), что позволяет избежать использования высокоточных аналоговых схем для фильтр сглаживания. Общий шум квантования одинаков как в преобразователе Найквиста (желтый), так и в преобразователе передискретизации (синий), но он распределен по другому спектру. В преобразователях ΔΣ шум дополнительно снижается на низких частотах, что является полосой, в которой находится интересующий сигнал, и увеличивается на более высоких частотах, где он может быть отфильтрован. Этот метод известен как формирование шума.
Для дельта-сигма-модулятора первого порядка шум формируется фильтром с передаточной функцией ЧАСп(z) = [1 − z−1]. Предполагая, что частота дискретизации жs большая по сравнению с интересующей частотой сигнала, ж0, шум квантования в полосе полезного сигнала можно аппроксимировать следующим образом:
- .
Аналогично для дельта-сигма-модулятора второго порядка шум формируется фильтром с передаточной функцией ЧАСп(z) = [1 − z−1]2. Шум внутриполосного квантования можно аппроксимировать следующим образом:
- .
В общем, для N- модулятора ΔΣ, дисперсия шума внутриполосного квантования составляет:
- .
Когда частота дискретизации увеличивается вдвое, отношение сигнал / шум квантования улучшается на 6N + 3 дБ для Nмодулятор ΔΣ-порядка. Чем выше коэффициент передискретизации, тем выше соотношение сигнал шум и чем выше разрешение в битах.
Другой ключевой аспект передискретизации - это компромисс между скоростью и разрешением. Децимационный фильтр, установленный после модулятора, не только фильтрует весь дискретизированный сигнал в интересующей полосе частот (устраняя шум на более высоких частотах), но также снижает частоту сигнала, увеличивая его разрешение. Это получается своего рода усреднение потока битов с более высокой скоростью передачи данных.
Именование
Этот метод был впервые представлен в начале 1960-х профессором Ясухико Ясуда, когда он был студентом Токийский университет.[13][14] Название дельта-сигма происходит непосредственно из-за наличия дельта-модулятора и интегратора, как впервые было введено Inose et al. в своей патентной заявке.[8] То есть название происходит от интеграции или подведение итогов различия, которые в математике представляют собой операции, обычно связанные с греческими буквами сигма и дельта соответственно. Оба имени сигма-дельта и дельта-сигма часто используются.
Смотрите также
Рекомендации
- ^ Сангил парк, Принципы сигма-дельта модуляции для аналого-цифровых преобразователей (PDF), Motorola, получено 2017-09-01
- ^ Дж. Кэнди и О. Бенджамин (сентябрь 1981 г.). «Структура шума квантования от сигма-дельта модуляции». Транзакции IEEE по коммуникациям. 29 (9): 1316–1323. Дои:10.1109 / TCOM.1981.1095151.CS1 maint: использует параметр авторов (связь)
- ^ Киккерт, К. Дж., И Д. Дж. Миллер (1975). «Асинхронная дельта-сигма-модуляция». Труды института инженеров радио и электроники. 36: 83–88. Получено 19 февраля 2019.CS1 maint: несколько имен: список авторов (связь)
- ^ Гаггл, Ричард (2012). Аналого-цифровые преобразователи Delta-Sigma. Springer. С. 41–45. ISBN 9783642345432. Получено 19 февраля 2019.
- ^ Мичил А.П. Пертижс и Йохан Хейзинг (2006). Прецизионные датчики температуры в КМОП-технологии. Springer. С. 111–113. ISBN 9781402052583.CS1 maint: использует параметр авторов (связь)
- ^ «Эволюция аналого-цифровых преобразователей с передискретизацией» Брюс А. Вули
- ^ Ф. де Ягер, «Дельта-модуляция, метод передачи ИКМ с использованием кода с 1 единицей», Philips Res. Rep., Т. 7. С. 442–466, 1952.
- ^ а б Х. Инозе, Ю. Ясуда, Дж. Мураками, "Система телеметрии путем манипулирования кодом - ΔΣ-модуляция", IRE Trans on Space Electronics and Telemetry, сентябрь 1962 г., стр. 204-209.
- ^ "Синтезатор фракционного N 15-25 МГц".
- ^ Новая архитектура для сбора данных в многоканальном TPC с жидким аргоном с большим объемом и длинным дрейфом С. Центро, Г. Менг, Ф. Пьетропаола, С. Вентура, 2006 г.
- ^ Lombardi, A .; Bonizzoni, E .; Malcovati, P .; Малоберти, Ф. (2007). "Низкое энергопотребление"3 Фильтр для ΣΔ Модуляторов ». 2007 Международный симпозиум IEEE по схемам и системам. С. 4008–4011. Дои:10.1109 / ISCAS.2007.378797. ISBN 978-1-4244-0920-4. S2CID 18354732.
- ^ Сигма-дельта-усилитель класса D и метод управления для сигма-дельта-усилителя класса D Джвин-Йен Го и Тэн-Хун Чанг
- ^ 発 見 と 発 明 の デ ジ タ 博物館 デ ー タ ベ ー ス ・ 気 ・ 情報 通信 関 研究 情報 (登録 番号 671)
- ^ Сангил парк, Принципы сигма-дельта модуляции для аналого-цифровых преобразователей (PDF), Motorola, заархивировано из оригинал (PDF) на 2006-06-21
- Уолт Кестер (октябрь 2008 г.). «Архитектура АЦП III: Основы сигма-дельта АЦП» (PDF). Аналоговые устройства. Получено 2010-11-02.
- Р. Джейкоб Бейкер (2009). КМОП схема со смешанными сигналами (2-е изд.). Wiley-IEEE. ISBN 978-0-470-29026-2.
- Р. Шрайер; Г. Темес (2005). Понимание преобразователей данных дельта-сигма. ISBN 978-0-471-46585-0.
- С. Норсуорси; Р. Шрайер; Г. Темес (1997). Преобразователи данных дельта-сигма. ISBN 978-0-7803-1045-2.
- Дж. Кэнди; Г. Темес (1992). Преобразователи дельта-сигма данных с передискретизацией. ISBN 978-0-87942-285-1.
внешняя ссылка
- 1-битные аналого-цифровые и цифро-аналоговые преобразователи
- Сигма-дельта методы расширяют разрешение ЦАП статья Тима Уэскотта 23.06.2004
- Учебное пособие по проектированию модуляторов дельта-сигма: Часть I[мертвая ссылка ] и Часть II[мертвая ссылка ] Минглян (Майкл) Лю
- Публикации Габора Темеса
- Учебник по сигма-дельта-модуляции, часть II Содержит блок-схемы, код и простые объяснения
- Пример модели Simulink и скриптов для сигма-дельта АЦП с непрерывным временем Содержит пример кода Matlab и модель Simulink
- Проекты Брюса Вули по преобразованию дельта-сигма
- Введение в преобразователи дельта-сигма (который охватывает как сигма-дельта АЦП, так и ЦАП)
- Демистификация сигма-дельта АЦП. Эта подробная статья посвящена теории аналого-цифрового преобразователя Delta-Sigma.
- Однобитовое дельта-сигма цифро-аналоговое преобразование, часть I: теория статья Рэнди Йейтса, представленная на конференции comp.dsp 2004 г.
- Структура MASH (Multi-stAge noise SHaping) как с теорией, так и с блочной реализацией MASH
- Архитектура схемы фильтра формирования шума сигма-дельта АЦП с непрерывным временем обсуждает архитектурные компромиссы для непрерывных сигма-дельта-шумоподавляющих фильтров
- Преобразователи дельта-сигма: модуляция - интуитивная мотивация того, почему работает дельта-сигма модулятор
- Цифровой акселерометр с контролем обратной связи с использованием сигма-дельта модуляции

















