Хаотическое рассеяние - Википедия - Chaotic scattering

Хаотическое рассеяние это филиал теория хаоса иметь дело с рассеяние системы, демонстрирующие сильную чувствительность к начальным условиям. В классической системе рассеяния будет один или несколько параметры удара, б, в котором частица попадает в рассеиватель. Это вызывает один или несколько параметров выхода, у, когда частица уходит на бесконечность. Пока частица проходит через систему, может также произойти Время задержки, Т- время, необходимое частице для выхода из системы, - помимо пройденного расстояния, s, который в некоторых системах, то есть в «биллиардных» системах, в которых частица без потерь испытывает столкновения с жесткий, фиксированные объекты, эти два будут эквивалентны - см. ниже. В хаотической системе рассеяния мельчайшее изменение прицельного параметра может вызвать очень большое изменение выходных параметров.

Система Гаспара – Райса

Рис. 1: Схема системы рассеяния Гаспара – Райса, показывающая основные параметры.

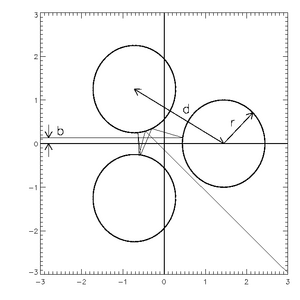
Прекрасным примером системы является система рассеяния "Гаспара – Райса" (GR).^[1]- также известная просто как система «трех дисков», которая воплощает в себе многие важные концепции хаотического рассеяния, будучи простой и легкой для понимания и моделирования. Идея очень проста: у нас есть три жестких диска, расположенных в некоторой треугольной формации, точечная частица отправляется и проходит безупречно, упругие столкновения пока не уйдет в бесконечность. В этом обсуждении мы будем рассматривать только системы ОТО с дисками одинакового размера, равномерно расположенными вокруг точек равностороннего треугольника.

На рисунке 1 показана эта система, а на рисунке 2 показаны два примера траекторий. Во-первых, обратите внимание, что траектории колеблются вокруг системы в течение некоторого времени, прежде чем наконец выйти. Также обратите внимание, что если мы рассматриваем параметры удара как начало двух идеально горизонтальных линий слева (система полностью обратима: точка выхода также может быть точкой входа), две траектории изначально настолько близки, что почти идентичны. К моменту выхода они совершенно другие, что свидетельствует о сильной чувствительности к начальным условиям. Эта система будет использоваться в качестве примера на протяжении всей статьи.

Рис. 2: Система рассеяния Гаспара – Райса, демонстрирующая чувствительность к начальным условиям.

Скорость распада

Если мы введем большое количество частиц с равномерно распределенными прицельными параметрами, скорость, с которой они покидают систему, называется скоростью распада. Мы можем рассчитать скорость распада, моделируя систему в течение многих испытаний и формируя гистограмму времени задержки, Т. Для системы ОТО легко видеть, что время задержки и длина траектории частицы эквивалентны, но для коэффициента умножения. Типичный выбор прицельного параметра - это у-координата, в то время как угол траектории поддерживается постоянным на нуле градусов - по горизонтали. Между тем, мы говорим, что частица «вышла из системы», когда она пересекает границу на некотором произвольном, но достаточно большом расстоянии от центра системы.

Мы ожидаем количество частиц, оставшихся в системе, N (Т), варьироваться как:

${ Displaystyle N (T) sim e ^ {- gamma T}}$

Таким образом скорость распада, ${ displaystyle gamma}$, определяется как:

${ displaystyle gamma = lim _ {n rightarrow infty} - { frac { ln N (T)} {T}}}$

куда п - общее количество частиц.^[2]

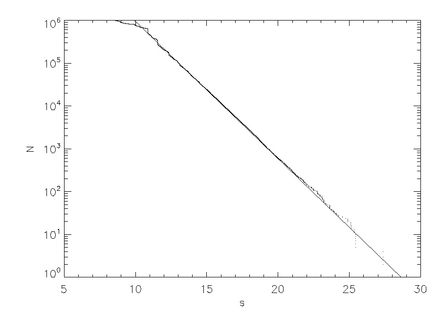
На рисунке 3 показан график зависимости длины пути от числа частиц для моделирования одного миллиона (1e6) частиц, запущенных со случайным прицельным параметром, б. Подгоняемая прямая отрицательного наклона, ${ displaystyle gamma = 0,739}$ накладывается. Длина пути, s, эквивалентно времени затухания, Тпри условии, что мы соответствующим образом масштабируем (постоянную) скорость. Обратите внимание, что экспоненциальная скорость затухания - это особенность гиперболического хаотического рассеяния. Негиперболические рассеиватели могут иметь арифметическую скорость затухания.^[3]

Рис. 3: Скорость затухания системы рассеяния Гаспара – Райса.

Экспериментальная система и устойчивое многообразие

Рис. 4: Экспериментальная система рассеяния Гаспара – Райса. ^[4]

На рисунке 4 показана экспериментальная реализация системы Гаспара – Райса с использованием лазера вместо точечной частицы. Любой, кто действительно пробовал это сделать, знает, что это не очень эффективный метод тестирования системы - лазерный луч рассеивается во всех направлениях. Как показали Свит, Отт и Йорк,^[5] Более эффективный метод - направить цветной свет через промежутки между дисками (или, в данном случае, приклеить цветные полосы бумаги через пары цилиндров) и увидеть отражения через открытый промежуток. В результате получается сложный узор из чередующихся полос. цвет, показанный ниже, более четко виден в смоделированной версии ниже.

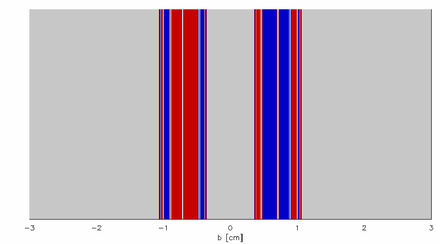
На рисунках 5 и 6 показаны бассейны притяжения для каждого параметра удара, б, то есть для данного значения бчерез какой промежуток выходит частица? В границы бассейна сформировать Кантор набор и представляют членов стабильное многообразие: траектории, которые, однажды начавшись, никогда не выходят из системы.

Рис. 5: Экспериментальная система рассеяния Гаспара – Райса, показывающая области притяжения.^[4]

Рис. 6: Моделирование системы рассеяния Гаспара – Райса, показывающее области притяжения.^[4]

Инвариантное множество и символическая динамика

Рис. 7: Возможные переменные для представления системы Гаспара – Райса в виде повторяющейся карты функций.^[6]

Пока она симметрична, мы можем легко думать о системе как о повторяющаяся функция карта, распространенный метод представления хаотической динамической системы. ^[7]На рисунке 7 показано одно возможное представление переменных с первой переменной, ${ Displaystyle тета в [- пи, пи]}$, представляющий угол вокруг диска при отскоке, а второй, ${ Displaystyle фи в [- пи / 2, пи / 2]}$, представляющий угол удара / отскока относительно диска. Подмножество этих двух переменных, называемое инвариантный набор будут отображены на самих себя. Этот набор, четыре члена которого показаны на рисунках 8 и 9, будет фрактал, совершенно не привлекающий мера нуль. Это интересная инверсия обычно обсуждаемых хаотических систем, в которых фрактальное инвариантное множество притягивает и фактически включает в себя бассейн (ы) притяжения. Обратите внимание, что совершенно не притягивающий характер инвариантного множества - еще одно свойство гиперболического хаотического рассеивателя.

Рис. 8: Четыре члена инвариантного множества системы Гаспара – Райса.

Рис. 9: Четыре члена инвариантного набора системы Гаспара – Райса, повторяемые вперед во времени.

Каждый член инвариантного набора можно смоделировать с помощью символическая динамика: траектория помечается на основе каждого диска, от которого она отскакивает. совокупность всех таких последовательностей образует бесчисленное множество.^[8]Для четырех элементов, показанных на рисунках 8 и 9, символическая динамика будет следующей:^[3]

...121212121212......232323232323......313131313131......123123123123...

Аналогичным образом могут быть представлены члены стабильного многообразия, за исключением того, что каждая последовательность имеет начальную точку. Если учесть, что член инвариантного множества должен «вписываться» в границы между двумя бассейнами притяжения, очевидно, что в случае возмущения траектория может выйти в любом месте последовательности. Таким образом, также должно быть очевидно, что бесконечное количество чередующихся бассейнов всех трех «цветов» будет существовать между любой данной границей.^[2][3][8]

Из-за их нестабильной природы трудно получить прямой доступ к членам инвариантного множества или стабильного многообразия. В показатель неопределенности идеально подходит для измерения фрактальной размерности систем этого типа. Еще раз используя параметр одиночного удара, б, мы проводим несколько испытаний со случайными параметрами удара, меняя их на минутную величину, ${ displaystyle epsilon}$, и подсчет того, как часто изменяется количество отскоков от дисков, то есть доля неопределенности. Обратите внимание, что даже если система является двумерной, одного параметра удара достаточно для измерения фрактальной размерности устойчивого коллектора. Это продемонстрировано на Рисунке 10, на котором показаны бассейны притяжения как функция двойного прицельного параметра: ${ displaystyle theta}$ и ${ displaystyle phi}$. Устойчивое многообразие, которое можно увидеть на границах между бассейнами, фрактально только в одном измерении.

Рис.10: Бассейны притяжения как функция параметров двойного удара. ${ displaystyle theta}$ и ${ displaystyle phi}$. ^[6]

На рисунке 11 показана доля неопределенности, ж, как функция неопределенности, ${ displaystyle epsilon}$ для моделируемой системы Гаспара – Райса. Наклон подобранной кривой возвращает показатель неопределенности, ${ displaystyle gamma = 0,380}$, Таким образом размер подсчета коробок устойчивого многообразия есть, ${ displaystyle D_ {0} = N- gamma = 2-0,380 = 1,62}$. Инвариантное множество - это пересечение стабильной и неустойчивые коллекторы.^[9]

Поскольку система одинакова независимо от того, движется вперед или назад, неустойчивое многообразие является просто зеркальным отображением устойчивого многообразия, и их фрактальные размеры будут равны.^[8]Исходя из этого, мы можем вычислить фрактальную размерность инвариантного множества:^[2]

${ Displaystyle D = D_ {s} + D_ {u} -N = 2D_ {s} -N = N-2 gamma}$

куда D_s и D_u - фрактальные размерности устойчивого и неустойчивого многообразий соответственно и N= 2 - размерность системы. Фрактальная размерность инвариантного множества равна D=1.24.

Рис. 10: График доли неопределенности системы рассеяния Гаспара – Райса с аппроксимацией прямой линией, что дает показатель неопределенности.

Связь фрактальной размерности, скорости распада и показателей Ляпунова

Из предыдущего обсуждения должно быть очевидно, что скорость распада, фрактальная размерность и Показатели Ляпунова все связаны. Например, большой показатель Ляпунова говорит нам, насколько быстро траектория в инвариантном множестве будет расходиться при возмущении. Точно так же фрактальная размерность даст нам информацию о плотности орбит в инвариантном множестве. Таким образом, мы можем видеть, что и то и другое будет влиять на скорость распада, как зафиксировано в следующей гипотезе для двумерной системы рассеяния:^[2]

${ displaystyle D_ {1} = left (h_ {1} - { frac {1} { gamma}} right) left ({ frac {1} {h_ {1}}} - { frac {1} {h_ {2}}} right)}$

куда D₁ это информационное измерение и ч₁ и ч₂ - соответственно малый и большой показатели Ляпунова. Для аттрактора ${ displaystyle gamma = infty}$ и сводится к Гипотеза Каплана – Йорка.^[2]

Смотрите также

• Озера Вада
• Показатель неопределенности

Рекомендации

внешняя ссылка

• Программное обеспечение для моделирования системы Гаспара – Райса.