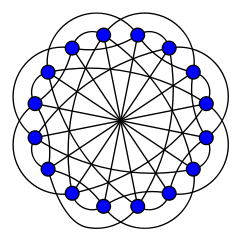
Граф Клебша - Clebsch graph

Граф Клебша
Clebsch Lombardi.svg
Названный в честьАльфред Клебш
Вершины16
Края40
Радиус2
Диаметр2
Обхват4
Автоморфизмы1920
Хроматическое число4[1]
Хроматический индекс5
Толщина книги4
Номер очереди3
ХарактеристикиСильно регулярный
Гамильтониан
Граф Кэли
Вершинно-транзитивный
Edge-транзитивный
Дистанционно-транзитивный.
Таблица графиков и параметров

в математический поле теория графов, то Граф Клебша один из двух дополнительный графы на 16 вершинах, 5-регулярный граф с 40 ребрами и 10-регулярный граф с 80 ребрами. Вариант с 80 кромками - это порядок-5. вдвое кубический граф; Зайдель (1968) назвал его именем графа Клебша.[2] из-за его связи с конфигурацией 16 линий на поверхности квартики, открытой в 1868 году немецким математиком Альфред Клебш. Вариант с 40 кромками - это порядок-5. свернутый куб граф; он также известен как График Гринвуда – Глисона после работы Роберта Э. Гринвуда и Эндрю М. Глисон  (1955 ), который использовал его для оценки Число Рамсея р(3,3,3) = 17.[3][4][5]

Строительство

Орден-5 свернутый куб граф (5-регулярный граф Клебша) может быть построен путем добавления ребер между противоположными парами вершин в 4-мерном графе гиперкуба. (В п-мерный гиперкуб, пара вершин противоположный если кратчайший путь между ними п ребер.) В качестве альтернативы, он может быть сформирован из 5-мерного графа гиперкуба с помощью идентификация вместе (или сжимая) каждую противоположную пару вершин.

Другая конструкция, приводящая к тому же графу, заключается в создании вершины для каждого элемента конечное поле GF (16), и соединить две вершины ребром всякий раз, когда разница между соответствующими двумя элементами поля равна идеальный куб.[6]

Орден-5 вдвое кубический граф (10-регулярный граф Клебша) - это дополнять 5-регулярного графа. Его также можно построить из вершин 5-мерного гиперкуба, соединяя пары вершин, у которых Расстояние Хэмминга ровно два. Эта конструкция является примером построения Графики Франкла – Рёдля. Он создает два подмножества по 16 вершин, которые не связаны друг с другом; Оба эти полуквадраты гиперкуба изоморфный к 10-регулярному графу Клебша. Две копии 5-регулярного графа Клебша могут быть созданы таким же образом из 5-мерного гиперкуба, соединяя пары вершин, расстояние Хэмминга которых равно четырем.

Характеристики

5-регулярный граф Клебша - это сильно регулярный граф степени 5 с параметрами .[7][8]Его дополнение, 10-регулярный граф Клебша, следовательно, также является сильно регулярным графом,[1][4] с параметрами .

5-регулярный граф Клебша имеет вид гамильтониан, непланарный и не эйлерово. Это также одновременно 5-вершинно-связанный и 5-реберный. В подграф, который индуцирован десятью несоседями любой вершины в этом графе образует изоморфный копия Граф Петерсена.

Она имеет толщина книги 4 и номер очереди 3.[9]

K16 Трехцветный, как три графика Клебша.

Края полный график K16 может быть разбит на три непересекающиеся копии 5-регулярного графа Клебша. Поскольку граф Клебша является граф без треугольников, это показывает, что существует трехкратная раскраска ребер K16; то есть, что Число Рамсея р(3,3,3), описывающее минимальное количество вершин в полном графе без трехцветной раскраски без треугольников, составляет не менее 17. Гринвуд и Глисон (1955) использовали эту конструкцию как часть своего доказательства того, что р(3,3,3) = 17.[5][10]

5-регулярный граф Клебша может быть цветной с четырьмя цветами, но не с тремя: самый большой независимый набор имеет пять вершин, чего недостаточно, чтобы разбить граф на три независимых цветовых класса. Он содержит как индуцированный подграф то График Грёча, наименьший без треугольников четыреххроматический граф, и каждый четыреххроматический индуцированный подграф графа Клебша является надграфом графа Грёча. Более того, каждый четыреххроматический граф без треугольников без индуцированный путь длины шесть и более является индуцированным подграфом графа Клебша и индуцированным суперграфом графа Грёча.[11]

5-регулярный граф Клебша - это Граф Келлера размерности два, часть семейства графов, используемых для поиска мозаик многомерных Евклидовы пространства к гиперкубы нет двух из которых встречаются лицом к лицу.

5-регулярный граф Клебша можно вложить как обычная карта в ориентируемом многообразии рода 5, образующем пятиугольные грани; и в неориентируемой поверхности рода 6, образующей тетрагональные грани.

Алгебраические свойства

В характеристический многочлен 5-регулярного графа Клебша есть . Поскольку этот многочлен может быть полностью разложен на линейные члены с целыми коэффициентами, граф Клебша является интегральный график: это спектр полностью состоит из целых чисел.[4] Граф Клебша - единственный граф с этим характеристическим полиномом, что делает его графом, определяемым его спектром.

5-регулярный граф Клебша - это Граф Кэли с группой автоморфизмов порядка 1920, изоморфной группе Группа Коксетера . Как граф Кэли, его группа автоморфизмов действует транзитивно на его вершинах, что делает его вершинно-транзитивный. На самом деле это переходная дуга, следовательно край переходный и переходное расстояние. Это также связно-однородный, означающее, что любой изоморфизм между двумя связными индуцированными подграфами можно продолжить до автоморфизма всего графа.

Галерея

Рекомендации

  1. ^ а б Вайсштейн, Эрик В. "График Клебша". Из MathWorld - веб-ресурса Wolfram. Получено 2009-08-13.
  2. ^ J. J. Seidel, Сильно регулярные графы с (-1,1,0) матрицей смежности, имеющей собственное значение 3, Lin. Alg. Appl. 1 (1968) 281-298.
  3. ^ Клебш, А. (1868), "Ueber die Flächen vierter Ordnung, welche eine Doppelcurve zweiten Grades besitzen", Журнал für die reine und angewandte Mathematik, 69: 142–184.
  4. ^ а б c График Клебша на домашней странице Билла Черовицо
  5. ^ а б Greenwood, R.E .; Глисон, А.М. (1955), «Комбинаторные отношения и хроматические графы», Канадский математический журнал, 7: 1–7, Дои:10.4153 / CJM-1955-001-4, МИСТЕР  0067467.
  6. ^ Де Клерк, Франк (1997). "Построения и характеристики (полу) частичных геометрий". Летняя школа по конечным геометриям. п. 6.
  7. ^ Годсил, К. (1995). «Проблемы алгебраической комбинаторики» (PDF). Электронный журнал комбинаторики. 2: 3. Получено 2009-08-13.
  8. ^ Питер Дж. Кэмерон Сильно регулярные графы на DesignTheory.org, 2001 г.
  9. ^ Джессика Вольц, Инженерные линейные схемы с SAT. Магистерская работа, Тюбингенский университет, 2018 г.
  10. ^ Sun, Hugo S .; Коэн, М. Э. (1984), "Простое доказательство оценки Гринвуда – Глисона числа Рамсея. р(3,3,3)" (PDF), Ежеквартальный отчет Фибоначчи, 22 (3): 235–238, МИСТЕР  0765316.
  11. ^ Рандерат, Берт; Ширмейер, Инго; Тьюис, Мейке (2002), "Трехкратность и запрещенные подграфы. II. Полиномиальные алгоритмы", Дискретная математика, 251 (1–3): 137–153, Дои:10.1016 / S0012-365X (01) 00335-1, МИСТЕР  1904597.