В уравнения коллинеарности представляют собой систему двух уравнений, используемых в фотограмметрия и компьютерное стереозрение, чтобы связать координаты в датчик плоскость (в двух измерениях) в координаты объекта (в трех измерениях). Уравнения происходят из центральная проекция точки объект сквозь оптический центр из камера к изображению на плоскости сенсора.[1]

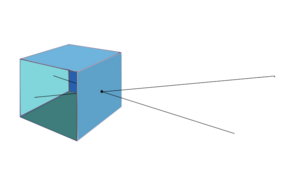
Три точки P, Q и R проецируются на плоскость S через центр проекции C.

Ось x и z проекции точки P через центр проекции C
Определение
Пусть x, y и z относятся к система координат с осями x и y в плоскости датчика. Обозначим координаты точки P на объекте как  , координаты точки изображения P на плоскости датчика на Икс и у а координаты проекционного (оптического) центра - на
, координаты точки изображения P на плоскости датчика на Икс и у а координаты проекционного (оптического) центра - на  . Как следствие метода проецирования есть такие же фиксированные соотношение
. Как следствие метода проецирования есть такие же фиксированные соотношение  между
между  и
и  ,
,  и
и  , а расстояние от центра проекции до плоскости датчика
, а расстояние от центра проекции до плоскости датчика  и
и  . Отсюда:
. Отсюда:



Решение для  в последнем уравнении и ввод его в другие дает:
в последнем уравнении и ввод его в другие дает:


Точка P обычно задается в некоторой системе координат "вне" камеры через координаты Икс, Y и Z, а центр проекции - на  . Эти координаты могут быть преобразованы через вращение и перевод к системе на камере. Перевод не влияет на разницу координат, а вращение, часто называемое преобразование камеры, задается 3 × 3-матрица р, преобразование
. Эти координаты могут быть преобразованы через вращение и перевод к системе на камере. Перевод не влияет на разницу координат, а вращение, часто называемое преобразование камеры, задается 3 × 3-матрица р, преобразование  в:
в:


и

Подстановка этих выражений приводит к набору двух уравнений, известных как уравнения коллинеарности:


Наиболее очевидное использование этих уравнений - для изображений, записанных камерой. В этом случае уравнение описывает преобразования из пространства объекта (X, Y, Z) в координаты изображения (x, y). Он составляет основу уравнений, используемых в регулировка связки. Они указывают на то, что точка изображения (на сенсорной пластине камеры), наблюдаемая точка (на объекте) и центр проекции камеры были совмещены при съемке изображения.
Смотрите также
использованная литература