Соединение четырех октаэдров со свободой вращения - Compound of four octahedra with rotational freedom
| Соединение четырех октаэдров со свободой вращения | |
|---|---|
 | |
| Тип | Равномерное соединение |
| Индекс | UC10 |
| Многогранники | 4 октаэдры |
| Лица | 8+24 треугольники |
| Края | 48 |
| Вершины | 24 |
| Группа симметрии | пиритоэдрический (Тчас) |
| Подгруппа ограничиваясь одной составляющей | 6-кратный неправильное вращение (S6) |
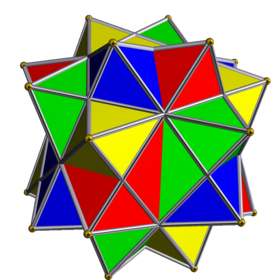
В соединение четырех октаэдров со свободой вращения это однородное соединение многогранника. Он состоит из симметричного расположения 4 октаэдры, считается треугольным антипризмы. Его можно построить, наложив четыре одинаковых октаэдра, а затем повернув каждый на равный угол. θ вокруг отдельной оси, проходящей через центры двух противоположных октаэдрических граней, таким образом, чтобы сохранить пиритоэдрический симметрия.
Наложение этого соединения на вторую копию, в которой октаэдры повернуты на тот же угол θ в обратном направлении дает соединение восьми октаэдров со свободой вращения.
Когда θ = 0, все четыре октаэдра совпадают. Когда θ 60 градусов, тем симметричнее соединение четырех октаэдров (без свободы вращения) возникает. В другом примечательном случае (на фото), когда
24 треугольника образуют компланарные пары, и соединение принимает форму соединение пяти октаэдров с удалением одного из октаэдров.
Галерея
Рекомендации
- Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79 (3): 447–457, Дои:10.1017 / S0305004100052440, Г-Н 0397554.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |














