Цепь Маркова с непрерывным временем - Continuous-time Markov chain
Эта статья включает Список ссылок, связанное чтение или внешняя ссылка, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
А цепь Маркова с непрерывным временем (CTMC) является непрерывным случайный процесс в котором для каждого состояния процесс будет изменять состояние в соответствии с экспоненциальная случайная величина а затем перейти в другое состояние, определяемое вероятностями стохастическая матрица. Эквивалентная формулировка описывает процесс как изменяющееся состояние в соответствии с наименьшим значением из набора экспоненциальных случайных величин, по одной для каждого возможного состояния, в которое он может перейти, с параметрами, определяемыми текущим состоянием.
Пример CTMC с тремя состояниями выглядит следующим образом: процесс выполняет переход по истечении времени, заданного параметром Время выдержки- экспоненциальная случайная величина , куда я его текущее состояние. Каждая случайная величина независима и такая, что , и . Когда необходимо произвести переход, процесс движется в соответствии с прыжковая цепь, а цепь Маркова с дискретным временем со стохастической матрицей:
Эквивалентно теорией конкурирующие экспоненты, этот CTMC меняет состояние из состояния я согласно минимуму двух независимых случайных величин, таких что за где параметры задаются Q-матрица
Каждое недиагональное значение может быть вычислено как произведение времени удержания исходного состояния на вероятность перехода в данное состояние из цепочки скачков. Значения диагонали выбираются так, чтобы сумма каждой строки равнялась 0.
CTMC удовлетворяет Марковская собственность, что его поведение зависит только от его текущего состояния, а не от его прошлого поведения из-за отсутствия памяти экспоненциального распределения и цепей Маркова с дискретным временем.
Определение
Цепь Маркова с непрерывным временем (Икст)т ≥ 0 определяется:[1]
- конечное или счетное пространство состояний S;
- а матрица скорости перехода Q с размерами, равными S; и
- начальное состояние такой, что , или распределение вероятностей для этого первого состояния.
За я ≠ j, элементы qij неотрицательны и описывают скорость перехода процесса из состояния я заявить j. Элементы qii могут быть выбраны равными нулю, но для математического удобства принято выбирать их так, чтобы каждая строка суммы к нулю, то есть:
Обратите внимание, как это отличается от определения матрицы перехода для дискретные цепи Маркова, где все суммы строк равны единице.
Есть три других определения процесса, эквивалентных приведенному выше.[2]
Определение вероятности перехода
Другой распространенный способ определения цепей Маркова с непрерывным временем состоит в том, чтобы вместо матрицы скорости перехода , используйте следующее:[1]
- , за , представляющий скорость распада (экспоненциального распределения), при котором система остается в состоянии как только он входит в него; и
- , за , представляющая вероятность того, что система перейдет в состояние , учитывая, что в настоящее время он покидает состояние .
Естественно, должен быть нулевым для всех .
Ценности и тесно связаны с матрицей скорости перехода , по формулам:
Рассмотрим упорядоченную последовательность моментов времени и состояния, записанные в это время , то считается, что:
- [сомнительный ]
где пij это решение прямое уравнение (а дифференциальное уравнение первого порядка ):
с начальным условием P (0), являющимся единичная матрица.
Бесконечно малое определение

Позволять случайная величина, описывающая состояние процесса во время т, и предположим, что процесс находится в состоянии я вовремя т.По определению цепи Маркова с непрерывным временем не зависит от значений до момента ; то есть не зависит от . Имея это в виду, для всех , для всех и при малых значениях , имеет место следующее:
- ,
куда это Дельта Кронекера и маленькая нотация был нанят.
Приведенное выше уравнение показывает, что можно рассматривать как измерение скорости перехода от к происходит для , и как быстро переход от происходит для .
Прыжковая цепь / определение времени удержания
Определите цепь Маркова с дискретным временем Yп описать пскачок процесса и переменных S1, S2, S3, ... для описания времени выдержки в каждом из состояний, где Sя следует экспоненциальному распределению с параметром скорости -qYяYя.
Характеристики
Общение на занятиях
Сообщающиеся классы, быстротечность, повторение, а также положительное и нулевое повторение определяются так же, как и для цепи Маркова с дискретным временем.
Переходное поведение
Напишите P (т) для матрицы с элементами пij = P (Икст = j | Икс0 = я). Тогда матрица P (т) удовлетворяет прямому уравнению, a дифференциальное уравнение первого порядка
где штрих означает дифференцирование по т. Решение этого уравнения дается матрица экспонента
В простом случае, таком как CTMC в пространстве состояний {1,2}. Генерал Q Матрица для такого процесса представляет собой следующую матрицу 2 × 2 с α,β > 0
Приведенное выше соотношение для прямой матрицы может быть решено явно в этом случае, чтобы дать
Однако прямые решения для больших матриц сложно вычислить. Дело в том, что Q является генератором для полугруппа матриц
используется.
Стационарное распределение
Стационарное распределение для неприводимого рекуррентного CTMC - это распределение вероятностей, к которому процесс сходится для больших значений т. Заметим, что для процесса с двумя состояниями, рассмотренного ранее с P (т) предоставлено
в качестве т → ∞ распределение стремится к
Обратите внимание, что каждая строка имеет одинаковое распределение, так как это не зависит от начального состояния. Вектор-строка π можно найти, решив[3]
с дополнительным ограничением, что
Пример 1
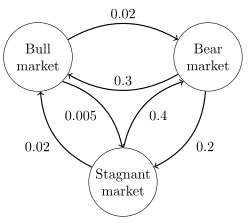
Изображение справа описывает цепь Маркова в непрерывном времени с пространством состояний {бычий рынок, медвежий рынок, застойный рынок} и матрица скорости перехода
Стационарное распределение этой цепочки можно найти, решив , при условии, что сумма элементов должна быть равна 1, чтобы получить
Пример 2
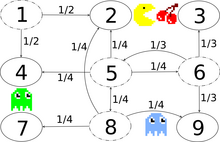
Изображение справа описывает моделирование цепи Маркова в дискретном времени. Pac-Man с пространством состояний {1,2,3,4,5,6,7,8,9}. Игрок управляет Пакманом через лабиринт, поедая пак-точки. Тем временем за ним охотятся призраки. Для удобства лабиринт представляет собой небольшую сетку 3x3, а монстры беспорядочно перемещаются в горизонтальном и вертикальном направлениях. Секретный проход между состояниями 2 и 8 можно использовать в обоих направлениях. Записи с нулевой вероятностью удаляются в следующей матрице перехода:
Эта цепь Маркова неприводима, потому что призраки могут перелететь из любого состояния в любое состояние за конечный промежуток времени. Из-за секретного прохода цепь Маркова также апериодична, потому что монстры могут переходить из любого состояния в любое состояние как при четном, так и при нечетном количестве переходов между состояниями. Следовательно, существует уникальное стационарное распределение, которое может быть найдено путем решения , при условии, что сумма элементов должна быть равна 1. Решение этого линейного уравнения с учетом ограничения имеет вид Центральное государство и пограничные состояния 2 и 8 соседнего секретного прохода посещаются чаще всего, а угловые состояния посещаются меньше всего.
Обратное время
Для CTMC Икст, обратный во времени процесс определяется как . К Лемма Келли этот процесс имеет такое же стационарное распределение, что и прямой процесс.
Цепочка называется обратимой, если обратный процесс такой же, как и прямой. Критерий Колмогорова утверждает, что необходимое и достаточное условие для того, чтобы процесс был обратимым, состоит в том, что произведение скоростей перехода по замкнутому контуру должно быть одинаковым в обоих направлениях.
Встроенная цепь Маркова
Один из способов найти стационарное распределение вероятностей, π, из эргодический цепь Маркова с непрерывным временем, Q, сначала найдя его встроенная цепь Маркова (EMC). Строго говоря, EMC - это обычная цепь Маркова с дискретным временем, которую иногда называют процесс прыжка. Каждый элемент матрицы вероятностей одношагового перехода EMC, S, обозначается sij, и представляет условная возможность перехода из состояния я в состояние j. Эти условные вероятности могут быть найдены
Из этого, S можно записать как
куда я это единичная матрица и диаг (Q) это диагональная матрица формируется путем выбора главная диагональ из матрицы Q и установка всех остальных элементов на ноль.
Чтобы найти вектор стационарного распределения вероятностей, мы должны найти такой, что
с вектор-строка, так что все элементы в больше 0 и = 1. Отсюда π можно найти как
(S может быть периодическим, даже если Q не является. Один раз π найден, его необходимо нормализовать до единичный вектор.)
Другой процесс с дискретным временем, который может быть получен из цепи Маркова с непрерывным временем, - это δ-скелет - цепь Маркова (с дискретным временем), образованная путем наблюдения Икс(т) с интервалом в δ единиц времени. Случайные величины Икс(0), Икс(δ),Икс(2δ), ... задают последовательность состояний, которые посещает δ-скелет.
Смотрите также
Примечания
- ^ а б Росс, С. (2010). Введение в вероятностные модели (10-е изд.). Эльзевир. ISBN 978-0-12-375686-2.
- ^ Норрис, Дж. Р. (1997). «Цепи Маркова с непрерывным временем I». Цепи Маркова. С. 60–107. Дои:10.1017 / CBO9780511810633.004. ISBN 9780511810633.
- ^ Норрис, Дж. Р. (1997). «Цепи Маркова с непрерывным временем II». Цепи Маркова. С. 108–127. Дои:10.1017 / CBO9780511810633.005. ISBN 9780511810633.
Рекомендации
- Марков А.А. (1971). «Распространение предельных теорем теории вероятностей на сумму переменных, соединенных в цепочку». перепечатано в Приложении B к: R. Howard. Динамические вероятностные системы, том 1: Марковские цепи. Джон Уайли и сыновья.
- Марков, А.А. (2006). Перевод Линка, Дэвид. "Пример статистического исследования текста Евгения Онегина о соединении образцов в цепочки". Наука в контексте. 19 (4): 591–600. Дои:10.1017 / s0269889706001074.
- Лео Брейман (1992) [1968] Вероятность. Оригинальное издание, опубликованное Эддисон-Уэсли; перепечатано Общество промышленной и прикладной математики ISBN 0-89871-296-3. (См. Главу 7)
- Дж. Л. Дуб (1953) Стохастические процессы. Нью-Йорк: Джон Уайли и сыновья ISBN 0-471-52369-0.
- С. П. Мейн и Р. Л. Твиди (1993) Марковские цепи и стохастическая устойчивость. Лондон: Springer-Verlag ISBN 0-387-19832-6. онлайн: MCSS . Выйдет второе издание, Cambridge University Press, 2009.
- Кемени, Джон Дж .; Хэзлтон Миркил; Дж. Лори Снелл; Джеральд Л. Томпсон (1959). Конечные математические структуры (1-е изд.). Энглвуд Клиффс, Нью-Джерси: Прентис-Холл, Инк. Номер каталога карточек Библиотеки Конгресса 59-12841. Классический текст. cf Глава 6 Конечные цепи Маркова стр. 384ff.
- Джон Г. Кемени & Дж. Лори Снелл (1960) Конечные цепи Маркова, D. van Nostrand Company ISBN 0-442-04328-7
- Э. Нуммелин. «Общие неприводимые цепи Маркова и неотрицательные операторы». Издательство Кембриджского университета, 1984, 2004. ISBN 0-521-60494-X
- Сенета, Э. Неотрицательные матрицы и цепи Маркова. 2-е изд. изд., 1981, XVI, 288 стр., Серия Springer в мягкой обложке по статистике. (Первоначально опубликовано Allen & Unwin Ltd., Лондон, 1973 г.) ISBN 978-0-387-29765-1
























































