Алгоритм Кули – Тьюки БПФ - Cooley–Tukey FFT algorithm

В Алгоритм Кули-Тьюки, названный в честь Дж. В. Кули и Джон Тьюки, является наиболее распространенным быстрое преобразование Фурье (БПФ) алгоритм. Он заново выражает дискретное преобразование Фурье (ДПФ) произвольной составной размер N = N₁N₂ с точки зрения N₁ ДПФ меньшего размера N₂, рекурсивно, чтобы сократить время вычислений до O (N бревно N) для высокосоставных N (гладкие числа ). Из-за важности алгоритма конкретные варианты и стили реализации стали известны под своими именами, как описано ниже.

Поскольку алгоритм Кули – Тьюки разбивает ДПФ на более мелкие ДПФ, его можно произвольно комбинировать с любым другим алгоритмом ДПФ. Например, Рейдера или же Bluestein's алгоритм может использоваться для обработки больших простых множителей, которые не могут быть разложены Кули-Тьюки, или алгоритм простого фактора можно использовать для большей эффективности при отделении относительно простой факторы.

Алгоритм, вместе с его рекурсивным применением, был изобретен Карл Фридрих Гаусс. Кули и Тьюки независимо друг от друга открыли и популяризировали его 160 лет спустя.

История

Этот алгоритм, включая его рекурсивное применение, был изобретен около 1805 г. Карл Фридрих Гаусс, который использовал его для интерполяции траекторий движения астероиды Паллада и Юнона, но его работа не получила широкого признания (опубликована только посмертно и в неолатинский ).^[1][2] Однако Гаусс не анализировал асимптотическое время вычисления. Различные ограниченные формы также были повторно открыты несколько раз на протяжении 19 и начала 20 веков.^[2] БПФ стали популярными после Джеймс Кули из IBM и Джон Тьюки из Принстон опубликовал в 1965 году статью, в которой заново изобрел алгоритм и описал, как удобно выполнять его на компьютере.^[3]

Тьюки, как сообщается, придумал эту идею во время встречи Научно-консультативного комитета президента Кеннеди, на котором обсуждались способы обнаружения испытания ядерного оружия в Советский союз используя сейсмометры, расположенные за пределами страны. Эти датчики будут генерировать сейсмологические временные ряды. Однако для анализа этих данных потребуются быстрые алгоритмы вычисления ДПФ из-за количества датчиков и продолжительности времени. Эта задача имела решающее значение для ратификации предложенного запрета на ядерные испытания, чтобы любые нарушения могли быть обнаружены без необходимости посещения советских объектов.^[4][5] Другой участник той встречи, Ричард Гарвин из IBM, осознали потенциал этого метода и связали Тьюки с Кули, убедившись, что Кули не знает первоначальной цели. Вместо этого Кули сказали, что это необходимо для определения периодичности ориентации спинов в трехмерном кристалле Гелий-3. Впоследствии Кули и Тьюки опубликовали свой совместный документ, который быстро получил широкое распространение благодаря одновременной разработке Аналого-цифровые преобразователи возможность дискретизации с частотой до 300 кГц.

Тот факт, что Гаусс описал тот же алгоритм (хотя и без анализа его асимптотической стоимости), был реализован лишь через несколько лет после статьи Кули и Тьюки 1965 года.^[2] В их статье в качестве вдохновения цитируется только работа И. Дж. Хорошо на том, что сейчас называется алгоритм БПФ с простым коэффициентом (PFA);^[3] Хотя алгоритм Гуда изначально считался эквивалентным алгоритму Кули-Тьюки, быстро стало понятно, что PFA - совсем другой алгоритм (работающий только для размеров, которые имеют относительно простой факторов и полагаясь на Китайская теорема об остатках, в отличие от поддержки любого составного размера в Кули – Тьюки).^[6]

Случай DIT Radix-2

А основание системы счисления-2 прореживание во времени (DITБПФ является самой простой и наиболее распространенной формой алгоритма Кули – Тьюки, хотя высокооптимизированные реализации Кули – Тьюки обычно используют другие формы алгоритма, как описано ниже. Radix-2 DIT делит ДПФ размера N на два чередующихся ДПФ (отсюда и название "основание-2") размера N/ 2 с каждым рекурсивным этапом.

Дискретное преобразование Фурье (ДПФ) определяется формулой:

${ displaystyle X_ {k} = sum _ {n = 0} ^ {N-1} x_ {n} e ^ {- { frac {2 pi i} {N}} nk},}$

куда ${ displaystyle k}$ целое число от ${ displaystyle 0}$ к ${ displaystyle N-1}$.

Radix-2 DIT сначала вычисляет ДПФ для входных данных с четным индексом${ Displaystyle (x_ {2m} = x_ {0}, x_ {2}, ldots, x_ {N-2})}$и входов с нечетной индексацией ${ Displaystyle (x_ {2m + 1} = x_ {1}, x_ {3}, ldots, x_ {N-1})}$, а затем объединяет эти два результата для получения ДПФ всей последовательности. Затем эту идею можно реализовать рекурсивно чтобы сократить общее время выполнения до O (N бревно N). Эта упрощенная форма предполагает, что N это сила двух; поскольку количество точек выборки N обычно может быть свободно выбран приложением (например, путем изменения частоты дискретизации или окна, заполнения нулями и т. д.), это часто не является важным ограничением.

Алгоритм Radix-2 DIT перестраивает ДПФ функции ${ displaystyle x_ {n}}$ на две части: сумма по четным индексам ${ displaystyle n = {2m}}$ и сумма по нечетным индексам ${ displaystyle n = {2m + 1}}$:

${ displaystyle { begin {matrix} X_ {k} & = & sum limits _ {m = 0} ^ {N / 2-1} x_ {2m} e ^ {- { frac {2 pi i) } {N}} (2m) k} + sum limits _ {m = 0} ^ {N / 2-1} x_ {2m + 1} e ^ {- { frac {2 pi i} {N }} (2m + 1) k} end {matrix}}}$

Можно множить общий множитель ${ displaystyle e ^ {- { frac {2 pi i} {N}} k}}$ из второй суммы, как показано в уравнении ниже. Тогда ясно, что две суммы являются ДПФ четно-индексированной части ${ displaystyle x_ {2m}}$ и ДПФ нечетно-индексированной части ${ displaystyle x_ {2m + 1}}$ функции ${ displaystyle x_ {n}}$. Обозначим ДПФ Eиндексированные по ven ${ displaystyle x_ {2m}}$ к ${ displaystyle E_ {k}}$ и ДПФ Оdd-индексированные входы ${ displaystyle x_ {2m + 1}}$ к ${ displaystyle O_ {k}}$ и получаем:

${ Displaystyle { begin {matrix} X_ {k} = underbrace { sum limits _ {m = 0} ^ {N / 2-1} x_ {2m} e ^ {- { frac {2 pi i} {N / 2}} mk}} _ { mathrm {DFT ; of ; с четным индексом ; part ; of ;} x_ {n}} {} + e ^ {- { frac { 2 pi i} {N}} k} underbrace { sum limits _ {m = 0} ^ {N / 2-1} x_ {2m + 1} e ^ {- { frac {2 pi i } {N / 2}} mk}} _ { mathrm {DFT ; of ; odd-indexed ; part ; of ;} x_ {n}} = E_ {k} + e ^ {- { гидроразрыв {2 pi i} {N}} k} O_ {k}. end {matrix}}}$

Благодаря периодичность комплексной экспоненты, ${ displaystyle X_ {k + { frac {N} {2}}}}$ также получается из ${ displaystyle E_ {k}}$ и ${ displaystyle O_ {k}}$:

${ displaystyle { begin {align} X_ {k + { frac {N} {2}}} & = sum limits _ {m = 0} ^ {N / 2-1} x_ {2m} e ^ { - { frac {2 pi i} {N / 2}} m (k + { frac {N} {2}})} + e ^ {- { frac {2 pi i} {N}} ( k + { frac {N} {2}})} sum limits _ {m = 0} ^ {N / 2-1} x_ {2m + 1} e ^ {- { frac {2 pi i} {N / 2}} m (k + { frac {N} {2}})} & = sum limits _ {m = 0} ^ {N / 2-1} x_ {2m} e ^ { - { frac {2 pi i} {N / 2}} mk} e ^ {- 2 pi mi} + e ^ {- { frac {2 pi i} {N}} k} e ^ { - pi i} sum limits _ {m = 0} ^ {N / 2-1} x_ {2m + 1} e ^ {- { frac {2 pi i} {N / 2}} mk} e ^ {- 2 pi mi} & = sum limits _ {m = 0} ^ {N / 2-1} x_ {2m} e ^ {- { frac {2 pi i} {N / 2}} mk} -e ^ {- { frac {2 pi i} {N}} k} sum limits _ {m = 0} ^ {N / 2-1} x_ {2m + 1} e ^ {- { frac {2 pi i} {N / 2}} mk} & = E_ {k} -e ^ {- { frac {2 pi i} {N}} k} O_ {к} конец {выровнено}}}$

Мы можем переписать ${ displaystyle X_ {k}}$ в качестве:

${ displaystyle { begin {matrix} X_ {k} & = & E_ {k} + e ^ {- { frac {2 pi i} {N}} {k}} O_ {k} X_ {k + { frac {N} {2}}} & = & E_ {k} -e ^ {- { frac {2 pi i} {N}} {k}} O_ {k} end {matrix}}}$

Этот результат, выражающий ДПФ длины N рекурсивно в терминах двух ДПФ размера N/ 2, является ядром быстрого преобразования Фурье Radix-2 DIT. Алгоритм набирает скорость за счет повторного использования результатов промежуточных вычислений для вычисления нескольких выходных данных ДПФ. Обратите внимание, что окончательные результаты получаются +/− комбинацией ${ displaystyle E_ {k}}$ и ${ Displaystyle О_ {к} ехр (-2 пи ik / N)}$, который представляет собой просто ДПФ размера 2 (иногда называемый бабочка в контексте); когда это обобщается для более крупных оснований ниже, ДПФ размера 2 заменяется ДПФ большего размера (которое само может быть оценено с помощью БПФ).

Схема потока данных для N= 8: БПФ с децимацией во времени по основанию 2 разбивает длинуN ДПФ на две длины-N/ 2 ДПФ, за которым следует этап комбинирования, состоящий из множества ДПФ размера 2, называемых операциями «бабочка» (так называемые из-за формы диаграмм потоков данных).

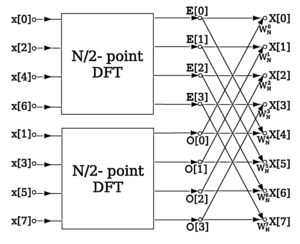
Этот процесс является примером общей техники разделяй и властвуй алгоритмы; однако во многих традиционных реализациях явная рекурсия избегается, и вместо этого выполняется обход вычислительного дерева в в ширину мода.

Вышеупомянутое перевыражение size-N ДПФ как два размера-N/ 2 ДПФ иногда называют Danielson –Ланцош лемма, поскольку идентичность была отмечена этими двумя авторами в 1942 г.^[7] (под влиянием Рунге 1903 г. работа^[2]). Они применяли свою лемму рекурсивно "назад", неоднократно удвоение размер ДПФ, пока спектр преобразования не сойдется (хотя они, по-видимому, не понимали линейный [т.е. заказ N бревноN] асимптотической сложности они достигли). Работа Дэниэлсона-Ланцоша предшествовала широкому распространению механические или электронные компьютеры и требуется ручной расчет (возможно, с помощью механических средств, таких как счетные машины ); они сообщили о времени вычисления 140 минут для ДПФ размером 64, работающего на реальные входы до 3–5 значащих цифр. В статье Кули и Тьюки 1965 г. сообщается, что время обработки сложного ДПФ размером 2048 составляет 0,02 минуты. IBM 7094 (вероятно, в 36-битном одинарная точность, ~ 8 цифр).^[3] Если изменить масштаб времени на количество операций, это примерно соответствует коэффициенту ускорения около 800000. (Чтобы представить время ручного вычисления в перспективе, 140 минут для размера 64 соответствуют в среднем максимум 16 секундам на операцию с плавающей запятой, около 20% из которых являются умножениями.)

Псевдокод

В псевдокод, можно написать следующую процедуру:^[8]

Икс0,...,N−1 ← ditfft2(Икс, N, s):             ДПФ из (x0, Иксs, Икс2s, ..., Икс(N-1)s):    если N = 1 тогда        Икс0 ← Икс0                                      тривиальный базовый случай ДПФ размера 1    еще        Икс0,...,N/2−1 ← ditfft2(Икс, N/2, 2s)             ДПФ из (x0, Икс2s, Икс4s, ...)        ИксN/2,...,N−1 ← ditfft2(Икс+ s, N/2, 2s)           ДПФ из (xs, Иксs+2s, Иксs+4s, ...)        за k = От 0 до N/2−1 делать                        объединить ДПФ двух половин в полное ДПФ:            t ← Иксk            Иксk ← t + exp (−2πя k/N) Иксk+N/2            Иксk+N/2 ← t - exp (−2πя k/N) Иксk+N/2        конец для    конец, если

Здесь, ditfft2(Икс,N, 1), вычисляет Икс= ДПФ (Икс) неуместный по основанию 2 DIT FFT, где N является целой степенью двойки и s= 1 - это шагать ввода Икс множество. Икс+s обозначает массив, начинающийся с Икс_s.

(Результаты находятся в правильном порядке в Икс и не дальше перестановка с обращением битов необходимо; часто упоминаемая необходимость отдельной стадии инвертирования битов возникает только для определенных алгоритмов на месте, как описано ниже.)

Высокопроизводительные реализации БПФ вносят множество изменений в реализацию такого алгоритма по сравнению с этим простым псевдокодом. Например, можно использовать более крупный базовый случай, чем N= От 1 до амортизировать накладные расходы на рекурсию, факторы поворота ${ Displaystyle ехр [-2 пи ik / N]}$ могут быть предварительно вычислены, и для тайник причины; вместе эти и другие оптимизации могут улучшить производительность на порядок или больше.^[8] (Во многих реализациях учебников в глубину рекурсия полностью устранена в пользу нерекурсивного в ширину подход, хотя утверждалось, что рекурсия в глубину лучше место в памяти.^[8][9]Некоторые из этих идей более подробно описаны ниже.

Идея

Основной шаг БПФ Кули – Тьюки для общих факторизаций можно рассматривать как переинтерпретацию 1d ДПФ как нечто вроде 2d ДПФ. 1d входной массив длины N = N₁N₂ интерпретируется как 2d N₁×N₂ матрица хранится в порядок столбцов. Один выполняет меньшие 1d ДПФ вдоль N₂ направление (несмежное направление), затем умножается на фазовые коэффициенты (коэффициенты вращения) и, наконец, выполняет 1d DFT вдоль N₁ направление. Шаг транспонирования может выполняться в середине, как показано здесь, или в начале или в конце. Это делается рекурсивно для небольших преобразований.

Иллюстрация порядка строк и столбцов

В более общем смысле, алгоритмы Кули – Тьюки рекурсивно повторно выражают ДПФ составного размера. N = N₁N₂ в качестве:^[10]

1. Выполнять N₁ ДПФ размера N₂.
2. Умножить на комплекс корни единства (часто называемый факторы поворота ).
3. Выполнять N₂ ДПФ размера N₁.

Обычно либо N₁ или же N₂ - небольшой фактор (нет обязательно простое), называемое основание (который может различаться между этапами рекурсии). Если N₁ это основание системы счисления, оно называется уничтожение во времени (DIT) алгоритм, тогда как если N₂ это основание, это децимация по частоте (DIF, также называемый алгоритмом Санде – Тьюки). Представленная выше версия была алгоритмом DIT с основанием 2; в окончательном выражении фаза, умножающая нечетное преобразование, представляет собой коэффициент вращения, а комбинация +/- (бабочка) четных и нечетных преобразований представляет собой ДПФ размера 2. (Малый ДПФ системы счисления иногда называют бабочка, так называемые из-за формы диаграмма потока данных для случая radix-2.)

Вариации

Есть много других вариантов алгоритма Кули – Тьюки. Смешанная система счисления реализации обрабатывают составные размеры с различными (обычно небольшими) факторами в дополнение к двум, обычно (но не всегда) используя O (N²) алгоритм для простых базовых случаев рекурсии (также можно использовать N бревноN алгоритм для простых базовых случаев, таких как Рейдер или Bluestein алгоритм). Разделение системы счисления объединяет основание системы счисления 2 и 4, используя тот факт, что первое преобразование системы счисления 2 не требует коэффициента поворота, чтобы достичь того, что долгое время было наименьшим известным числом арифметических операций для размеров степени двойки,^[10] хотя последние вариации достигают еще меньшего числа.^[11][12] (На современных компьютерах производительность определяется больше тайник и Конвейер процессора соображения, чем строгие подсчеты операций; Хорошо оптимизированные реализации БПФ часто используют большие радиусы и / или жестко закодированные преобразования базового случая значительного размера.^[13]).

Другой способ взглянуть на алгоритм Кули-Тьюки состоит в том, что он повторно выражает размер N одномерное ДПФ как N₁ к N₂ двумерное ДПФ (плюс тиддлы), где выходная матрица транспонированный. Чистый результат всех этих преобразований для алгоритма radix-2 соответствует инверсии битов входных (DIF) или выходных (DIT) индексов. Если вместо использования малой системы счисления используется система счисления примерно √N и явные транспозиции матриц ввода / вывода, это называется четырехступенчатый алгоритм (или шестиступенчатый, в зависимости от количества транспозиций), изначально предложенная для улучшения локальности памяти,^[14][15] например для оптимизации кеша или вне ядра операции, и позже было показано, что это оптимальный алгоритм, не обращающий внимания на кеш.^[16]

Общая факторизация Кули – Тьюки переписывает индексы k и п в качестве ${ displaystyle k = N_ {2} k_ {1} + k_ {2}}$ и ${ displaystyle n = N_ {1} n_ {2} + n_ {1}}$соответственно, где индексы k_а и п_а бежать с 0 ..N_а-1 (для а из 1 или 2). То есть он повторно индексирует ввод (п) и вывод (k) в качестве N₁ к N₂ двумерные массивы в столбец и рядовой порядок, соответственно; разница между этими индексами - это транспозиция, как упоминалось выше. Когда эта переиндексация подставляется в формулу ДПФ для нк, то ${ displaystyle N_ {1} n_ {2} N_ {2} k_ {1}}$ поперечный член обращается в нуль (его экспонента равна единице), а остальные члены дают

${ displaystyle X_ {N_ {2} k_ {1} + k_ {2}} = sum _ {n_ {1} = 0} ^ {N_ {1} -1} sum _ {n_ {2} = 0 } ^ {N_ {2} -1} x_ {N_ {1} n_ {2} + n_ {1}} e ^ {- { frac {2 pi i} {N_ {1} N_ {2}}} cdot (N_ {1} n_ {2} + n_ {1}) cdot (N_ {2} k_ {1} + k_ {2})}}$

${ displaystyle = sum _ {n_ {1} = 0} ^ {N_ {1} -1} left [e ^ {- { frac {2 pi i} {N_ {1} N_ {2}} } n_ {1} k_ {2}} right] left ( sum _ {n_ {2} = 0} ^ {N_ {2} -1} x_ {N_ {1} n_ {2} + n_ {1 }} e ^ {- { frac {2 pi i} {N_ {2}}} n_ {2} k_ {2}} right) e ^ {- { frac {2 pi i} {N_ { 1}}} n_ {1} k_ {1}}}$

${ displaystyle = sum _ {n_ {1} = 0} ^ {N_ {1} -1} left ( sum _ {n_ {2} = 0} ^ {N_ {2} -1} x_ {N_ {1} n_ {2} + n_ {1}} e ^ {- { frac {2 pi i} {N_ {2}}} n_ {2} k_ {2}} right) e ^ {- { frac {2 pi i} {N_ {1} N_ {2}}} n_ {1} (N_ {2} k_ {1} + k_ {2})}}$.

где каждая внутренняя сумма представляет собой ДПФ размера N₂, каждая внешняя сумма представляет собой ДПФ размером N₁, а член в квадратных [...] скобках - это фактор вращения.

Произвольная система счисления р (а также смешанные корни), как было показано Кули и Тьюки^[3] а также Гаусс (который привел примеры шагов с основанием системы счисления 3 и 6).^[2] Кули и Тьюки первоначально предположили, что корневая бабочка требует O (р²) работают и, следовательно, рассчитали сложность для системы счисления р быть O (р² N/р бревно_рN) = O (N бревно₂(N) р/бревно₂р); из расчета значений р/бревно₂р для целых значений р от 2 до 12 оптимальным основанием системы счисления является 3 (ближайшее целое число к е, что минимизирует р/бревно₂р).^[3][17] Однако этот анализ был ошибочным: основание-бабочка также является ДПФ и может быть выполнено с помощью алгоритма БПФ в O (р бревно р) операций, следовательно, основание системы счисления р фактически сокращается в сложности O (р бревно(р) N/р бревно_рN), а оптимальная р определяется более сложными соображениями. На практике довольно большой р (32 или 64) важны для эффективного использования, например, большое количество регистры процессора на современных процессорах,^[13] и даже безграничный основание р=√N также достигает O (N бревноN) сложность и имеет теоретические и практические преимущества для крупных N как уже упоминалось выше.^[14][15][16]

Переупорядочение данных, реверсирование битов и алгоритмы на месте

Хотя абстрактная факторизация Кули-Тьюки ДПФ, приведенная выше, применима в той или иной форме ко всем реализациям алгоритма, гораздо большее разнообразие существует в методах упорядочивания и доступа к данным на каждой стадии БПФ. Особый интерес представляет проблема создания алгоритм на месте который перезаписывает свои входные данные своими выходными данными, используя только вспомогательную память O (1).

Самый известный метод переупорядочения включает явное инверсия долота для алгоритмов с основанием 2 на месте. Разворот бит это перестановка где данные по индексу п, написано в двоичный с цифрами б₄б₃б₂б₁б₀ (например, 5 цифр для N= 32 входа), передается в индекс с перевернутыми цифрами б₀б₁б₂б₃б₄ . Рассмотрим последний этап алгоритма Radix-2 DIT, подобного представленному выше, где выходные данные записываются вместо входных: когда ${ displaystyle E_ {k}}$ и ${ displaystyle O_ {k}}$ комбинируются с ДПФ размера 2, эти два значения перезаписываются выходами. Однако два выходных значения должны идти в первом и втором половинки выходного массива, соответствующего наиболее значащий бит б₄ (за N= 32); тогда как два входа ${ displaystyle E_ {k}}$ и ${ displaystyle O_ {k}}$ чередуются по четным и нечетным элементам, соответствующим наименее значащий бит б₀. Таким образом, чтобы получить результат в правильном месте, б₀ должен занять место б₄ и индекс становится б₀б₄б₃б₂б₁. И для следующего рекурсивного этапа эти 4 младших бита станут б₁б₄б₃б₂, Если вы включите все рекурсивные этапы алгоритма Radix-2 DIT, все биты должны быть поменяны местами, и поэтому необходимо предварительно обработать ввод (или же постобработка вывода) с небольшим изменением направления, чтобы получить упорядоченный вывод. (Если каждый размер-NПодпреобразование / 2 предназначено для работы с непрерывными данными, DIT Вход предварительно обрабатывается обращением битов.) Соответственно, если вы выполните все шаги в обратном порядке, вы получите алгоритм DIF с основанием 2 с обращением битов при постобработке (или предварительной обработке, соответственно).

Логарифм (log), используемый в этом алгоритме, является логарифмом по основанию 2.

Ниже приводится псевдокод для итеративного алгоритма БПФ с основанием 2, реализованного с использованием перестановки с обращением битов.^[18]

алгоритм iterative-fft является    Вход: Множество а из п комплексные значения, где n - степень двойки. выход: Множество А ДПФ файла. бит-обратная копия (а, А) п ← а.длина за s = 1 к бревно(п) делать        м ← 2s        ωм ← exp (−2πя/м)         за k = 0 к п-1 к м делать            ω ← 1            за j = 0 к м/2 – 1 делать                т ← ω А[k + j + м/2]                ты ← А[k + j]                А[k + j] ← ты + т                А[k + j + м/2] ← ты – т                ω ← ω ωм       возвращаться А

Процедура битового обратного копирования может быть реализована следующим образом.

алгоритм бит-обратная копия (а,А) является    Вход: Множество а из п комплексные значения, где n - степень двойки. выход: Множество А размера п.    п ← а.длина за k = 0 к п – 1 делать        А[rev (k)]: = а[k]

В качестве альтернативы, некоторые приложения (например, свертка) одинаково хорошо работают с данными с обратным битом, поэтому можно выполнять прямые преобразования, обработку, а затем обратные преобразования, все без обращения битов, чтобы получить конечные результаты в естественном порядке.

Однако многие пользователи БПФ предпочитают выходные данные в естественном порядке, а отдельный этап явного обращения битов может оказать существенное влияние на время вычислений.^[13] хотя реверсирование битов может быть выполнено за O (N) времени и был предметом многих исследований.^[19][20][21] Кроме того, в то время как перестановка представляет собой инверсию битов в случае основания 2, в более общем случае это произвольное (смешанное основание) обращение цифр для случая смешанного основания системы счисления, и алгоритмы перестановки становятся более сложными для реализации. Более того, во многих аппаратных архитектурах желательно переупорядочить промежуточные этапы алгоритма БПФ, чтобы они работали с последовательными (или, по крайней мере, более локализованными) элементами данных. С этой целью был разработан ряд альтернативных схем реализации для алгоритма Кули-Тьюки, которые не требуют отдельного обращения битов и / или включают дополнительные перестановки на промежуточных этапах.

Проблема значительно упрощается, если она неуместный: выходной массив отличается от входного массива, или, что то же самое, доступен вспомогательный массив равного размера. В Stockham автосортировка алгоритм^[22][23] выполняет каждый этап БПФ не на своем месте, обычно записывая туда и обратно между двумя массивами, транспонируя одну «цифру» индексов на каждом этапе, и был особенно популярен на SIMD архитектуры.^[23][24] Еще большие потенциальные преимущества SIMD (более последовательные доступы) были предложены для Pease алгоритм,^[25] который также меняет порядок на каждом этапе, но этот метод требует отдельного обращения бит / цифра и O (N бревно N) место хранения. Также можно напрямую применить определение факторизации Кули – Тьюки с явным (в глубину ) рекурсии и малых оснований, которые производят вывод естественного порядка вне места без отдельного шага перестановки (как в псевдокоде выше), и можно утверждать, что не обращающий внимания на тайник преимущества местоположения в системах с иерархическая память.^[9][13][26]

Типичная стратегия для алгоритмов на месте без вспомогательной памяти и без отдельных проходов реверсирования цифр включает небольшие перестановки матриц (которые меняют местами отдельные пары цифр) на промежуточных этапах, которые можно комбинировать с бабочками системы счисления для уменьшения количества проходов по данные.^{[13][27][28][29][30]}

Рекомендации

внешняя ссылка

• «Быстрое преобразование Фурье - БПФ». Техника Кули-Тьюки. Статья. 10. Простой педагогический алгоритм radix-2 на C ++
• "KISSFFT". GitHub. Простая реализация Кули – Тьюки со смешанным основанием на языке C
• Dsplib на GitHub
• «Алгоритм прореживания Radix-2 во временном БПФ». Архивировано из оригинал 31 октября 2017 г. "Алгоритм БПФ по основанию два с прореживанием по времени" (на русском).
• "Прореживание Radix-2 в алгоритме частотного БПФ". Архивировано из оригинал 14 ноября 2017 г. "Алгоритм БПФ по основанию два с прореживанием по частотам" (на русском).