Ползучесть и усадка бетона - Creep and shrinkage of concrete

Эта статья включает список литературы, связанное чтение или внешние ссылки, но его источники остаются неясными, потому что в нем отсутствует встроенные цитаты. Пожалуйста, помогите улучшить эта статья введение более точные цитаты. (Июнь 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения)

Ползучесть и усадка бетона два физических свойства бетона. В ползать бетона, который происходит из гидраты силиката кальция (C-S-H) в закаленном портландцемент паста (которая является связующим веществом минеральных заполнителей) принципиально отличается от ползучести металлов и полимеров. В отличие от ползучести металлов, она вообще стресс уровней и, в пределах диапазона рабочих нагрузок, линейно зависит от напряжения, если содержание воды в порах является постоянным. В отличие от ползучести полимеров и металлов, он проявляет многомесячное старение, вызванное химическим упрочнением из-за гидратация что укрепляет микроструктура, и многолетнее старение, вызванное длительной релаксацией самоуравновешенных микронапряжений в нанопористой микроструктуре C-S-H. Если бетон полностью высох, он не ползет, но полностью высушить бетон без сильных трещин практически невозможно.

рисунок 1

Изменения содержания воды в порах из-за процессов сушки или смачивания вызывают значительные изменения объема бетона в образцах без нагрузки. Они называются усадкой (обычно вызывающей деформации от 0,0002 до 0,0005, а в бетонах с низкой прочностью даже 0,0012) или набуханием (<0,00005 для обычных бетонов, <0,00020 для высокопрочных бетонов). Чтобы отделить усадку от ползучести, функция податливости ${ Displaystyle J (т, т ')}$, определяемая как деформация, вызванная напряжением ${ displaystyle epsilon}$ (т. е. общая деформация минус усадка), вызванная в момент времени t единичным выдерживаемым одноосным напряжением ${ displaystyle sigma = 1}$ применяется в возрасте ${ displaystyle t '}$, измеряется как разница деформаций между нагруженными и ненагруженными образцами.

Многолетняя ползучесть эволюционирует во времени логарифмически (без окончательного асимптотического значения), и в течение типичного срока службы конструкции она может достигать значений, в 3-6 раз превышающих начальную упругую деформацию. Когда деформация внезапно возникает и остается постоянной, ползучесть вызывает релаксацию критически созданного упругого напряжения. После разгрузки происходит восстановление ползучести, но частичное из-за старения.

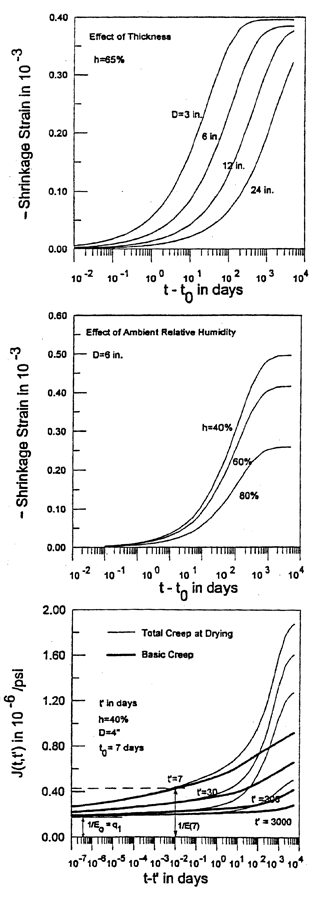
На практике ползучесть при сушке неотделима от усадки. Скорость ползучести увеличивается со скоростью изменения влажности пор (т. Е. Относительного давления пара в порах). Для образцов малой толщины ползучесть при сушке значительно превышает сумму усадки при сушке без нагрузки и ползучести нагруженного герметичного образца (рис. 1 внизу). Разница, называемая ползучесть при высыхании или эффект Пикетта (или усадка, вызванная напряжением), представляет собой гигромеханическую связь между изменениями деформации и влажности пор.

Усадка при высыхании при высокой влажности (рис. 1 вверху и в середине) вызывается в основном сжимающими напряжениями в твердой микроструктуре, которые уравновешивают увеличение капиллярного натяжения и поверхностного натяжения на стенках пор. При низкой влажности пор (<75%) усадка вызывается уменьшением расклинивающего давления через нанопоры толщиной менее 3 нм, заполненные адсорбированной водой.

Химические процессы гидратации портландцемента приводят к другому типу усадки, называемой автогенной усадкой, которая наблюдается в запечатанных образцах, то есть без потери влаги. Частично это вызвано химическими изменениями объема, но главным образом самовысыханием из-за потери воды, потребляемой реакцией гидратации. Это составляет лишь около 5% усадки при высыхании в обычных бетонах, которые самовысыхают до около 97% пористой влажности. Но он может равняться усадке при высыхании в современных высокопрочных бетонах с очень низким водоцементным соотношением, которые могут самовысыхать даже при влажности 75%.

Ползучесть возникает из-за гидратов силиката кальция (C-S-H) затвердевшего портландцементного теста. Это вызвано скольжением из-за разрывов адгезии с восстановлением адгезии на соседних участках. C-S-H является сильно гидрофильным и имеет коллоидную микроструктуру, неупорядоченную от нескольких нанометров. Паста имеет пористость от 0,4 до 0,55 и огромную площадь внутренней поверхности, примерно 500 мкм.²/см³. Его основной компонент - гель гидрата трикальцийсиликата (3 CaO · 2 SiO₃ · 3 H₂0, короче C₃-S₂-ЧАС₃). Гель образует частицы коллоидных размеров, слабо связанные силами Ван-дер-Ваальса.

Физический механизм и моделирование все еще обсуждаются. Модель определяющего материала в нижеследующих уравнениях не единственная доступная, но в настоящее время имеет сильнейшее теоретическое обоснование и лучше всего соответствует всему диапазону доступных тестовых данных.

Соотношение напряжения и деформации при постоянной среде

В процессе эксплуатации напряжения в конструкциях составляют <50% прочности бетона, и в этом случае зависимость напряжения от деформации является линейной, за исключением поправок на микротрещины при изменении влажности пор. Таким образом, ползучесть может быть охарактеризована функцией податливости ${ Displaystyle J (т, т ')}$ (Рис. 2). Так как ${ displaystyle t '}$ увеличивается, значение ползучести для фиксированных ${ Displaystyle т-т '}$ уменьшается. Это явление, называемое старением, вызывает ${ displaystyle J}$ зависит не только от задержки во времени ${ Displaystyle т-т '}$ но на обоих ${ displaystyle t}$ и ${ displaystyle t '}$ отдельно. При переменном напряжении ${ Displaystyle sigma (т)}$, каждое приращение напряжения ${ Displaystyle { mbox {d}} sigma (т ')}$ применяется во время ${ displaystyle t '}$ производит историю штаммов ${ Displaystyle { mbox {d}} epsilon (t) = J (t, t ') { mbox {d}} sigma (t')}$. Линейность подразумевает принцип суперпозиции (введенный Больцманом, а в случае старения - Вольтеррой). Это приводит к (одноосной) зависимости напряжения от деформации линейной вязкоупругости при старении:

${ displaystyle epsilon (t) = int _ {t_ {1}} ^ {t} J (t, t ^ { prime}) { mbox {d}} sigma (t ^ { prime}) + epsilon ^ {0} (t)}$

(1)

Вот ${ displaystyle epsilon ^ {0}}$ обозначает деформацию усадки ${ displaystyle epsilon _ {ш}}$ с добавлением теплового расширения, если таковое имеется. Интеграл - это Stieltjesintegral, который допускает истории ${ Displaystyle sigma (т)}$ с прыжками; для временных интервалов без скачков можно установить ${ Displaystyle { mbox {d}} sigma (t ') = [{ mbox {d}} sigma (t') / { mbox {d}} t '] { mbox {d}} т '}$ для получения стандартного интеграла (римана). Когда история ${ displaystyle epsilon (t)}$ задано, то уравнение (1) представляет собой интегральное уравнение Вольтерра для ${ Displaystyle sigma (т)}$. Это уравнение не интегрируемо аналитически для реалистичных форм ${ Displaystyle J (т, т ')}$, хотя численное интегрирование несложно. Решение ${ Displaystyle sigma (т)}$ для напряжения ${ displaystyle epsilon = 1}$ навязывается в любом возрасте ${ displaystyle { hat {t}}}$ (и для ${ displaystyle epsilon ^ {0} = 0}$) называется функцией релаксации ${ Displaystyle R (т, { шляпа {т}})}$.

Чтобы обобщить уравнение. (1) к трехосному соотношению напряжение-деформация, можно предположить, что материал изотропный, с приблизительно постоянным коэффициентом Пуассона ползучести, ${ displaystyle nu приблизительно 0,18}$. Это дает объемные и девиаторные отношения напряжения и деформации, аналогичные уравнению. (1) в котором ${ Displaystyle J (т, т ')}$ заменяется функциями объемной и сдвиговой податливости:

${ displaystyle J_ {K} (t, t ^ { prime}) = 3 (1-2 nu) J (t, t ^ { prime}), ~~~ J_ {G} (t, t ^ { prime}) = 2 (1+ nu) J (t, t ^ { prime})}$

(2)

Рис. 2

При высоком напряжении закон ползучести оказывается нелинейным (рис. 2), но уравнение (1) остается применимым, если неупругая деформация из-за растрескивания с ее зависящим от времени ростом включена в ${ displaystyle epsilon ^ {0} (т)}$. Вязкопластическая деформация должна быть добавлена ​​к ${ displaystyle epsilon ^ {0} (т)}$ только в том случае, если все главные напряжения являются сжимающими, а наименьшее по величине намного больше, чем прочность на одноосное сжатие ${ displaystyle f_ {c} '}$.

При измерениях модуль упругости Юнга ${ displaystyle E}$ зависит не только от конкретного возраста ${ displaystyle t '}$ но также и от продолжительности теста, потому что кривая соответствия ${ Displaystyle J (т, т ')}$ в зависимости от продолжительности нагрузки ${ Displaystyle т-т '}$ имеет значительный наклон для всех длительностей, начиная с 0,001 с или менее. Следовательно, обычный модуль упругости Юнга должен быть получен как ${ Displaystyle Е (т ') = 1 / J (т' + дельта, т ')}$,где ${ displaystyle delta}$ - продолжительность теста. Ценности ${ displaystyle delta приблизительно 0,01}$ день и ${ displaystyle t '= 28}$ дней дают хорошее согласие со стандартизированным тестом ${ displaystyle E}$, в том числе рост ${ displaystyle E}$ как функция ${ displaystyle t '}$, а с широко используемой эмпирической оценкой ${ displaystyle E = 57 000 { mbox {psi}}}$ ${ displaystyle { sqrt {f '_ {c} / { mbox {psi}}}}}$ ${ displaystyle (1 { mbox {psi}} = 6895 { mbox {Pa}}, f_ {c} '= { mbox {прочность бетона на одноосное сжатие}})}$. Нулевая экстраполяция ${ displaystyle q_ {1} = J (t ', t') = lim _ { delta to 0} J (t '+ delta, t')}$ примерно не зависит от возраста, что делает ${ displaystyle q_ {1}}$ удобный параметр для определения ${ Displaystyle J (т, т ')}$.

Для ползучести при постоянном общем содержании воды, называемой базовой ползучестью, реалистичная форма скорости одноосной функции податливости (толстые кривые на рисунке 1 внизу) была получена из теории затвердевания:

${ displaystyle { dot {J}} (t, t ') = v ^ {- 1} (t) { dot {C}} _ ​​{g} ( theta) + 1 / eta _ {f }, ~~~ v ^ {- 1} (t) = q_ {2} left ( lambda _ {0} / t ​​right) ^ {m} + q_ {3}}$

(3)

${ displaystyle { dot {C}} _ ​​{g} ( theta) = { frac {n theta ^ {n-1}} { lambda _ {0} ^ {n} + theta ^ {n }}}, ~~~ theta = t-t ', ~~~ 1 / eta _ {f} = q_ {4} / t}$

(4)

где ${ displaystyle { dot {x}} = partial x / partial t}$; ${ displaystyle eta _ {f}}$ = вязкость потока, определяющая многолетнюю ползучесть; ${ displaystyle theta}$ = продолжительность нагрузки; ${ displaystyle lambda _ {0}}$ = 1 день, ${ displaystyle m = 0,5}$, ${ displaystyle n = 0,1}$; ${ displaystyle v (t) { rm {МПа ^ {- 1}}}}$ = объем геля на единицу объема бетона, растущий за счет гидратации; и ${ displaystyle q_ {2}, q_ {3}, q_ {4}}$ = эмпирические константы (размерности ${ displaystyle { rm {МПа ^ {- 1}}}}$). Функция ${ Displaystyle C_ {g} ( theta)}$ придает цементному гелю замедленную эластичность, не зависящую от возраста (затвердевшее цементное тесто без капиллярных пор), и за счет интеграции ${ displaystyle C_ {g} ( theta) = { mbox {ln}} [1 + ( theta / lambda _ {0}) ^ {n}]}$.Интеграция ${ Displaystyle { точка {J}} (т, т ')}$ дает ${ Displaystyle J (т, т ')}$ как неинтегрируемый биномиальный интеграл, и поэтому, если значения ${ Displaystyle J (т, т ')}$ ищутся, они должны быть получены путем численного интегрирования или аппроксимационной формулы (существует хорошая формула). Однако для компьютерного структурного анализа по временным шагам ${ Displaystyle J (т, т ')}$ не нужен; только скорость ${ Displaystyle { точка {J}} (т, т ')}$ необходим как вход.

Уравнения. (3) и (4) - простейшие формулы, удовлетворяющие трем требованиям: 1) Асимптотически как для коротких, так и для больших времен ${ displaystyle theta}$, ${ Displaystyle { точка {J}} (т, т ')}$, должна быть степенной функцией времени; и 2) скорость старения должна определяться как ${ displaystyle { rm {{ mbox {d}} v ^ {- 1} (t) / { mbox {d}} t}}}$) (степенные функции обозначены условиями самоподобия); и 3) ${ Displaystyle partial ^ {2} J (t, t ') / partial t partial t'> 0}$ (это условие требуется, чтобы принцип суперпозиции не давал немонотонных кривых восстановления после разгрузки, которые физически нежелательны).

Ползать в изменчивой среде

При переменной массе ${ displaystyle w}$ испаряемой (то есть химически не связанной) воды на единицу объема бетона, физически реалистичное определяющее соотношение может быть основано на идее микронапряжения ${ displaystyle S}$, который рассматривается как безразмерная мера пиков напряжения в местах ползучести микроструктуры. Микропрессование возникает как реакция на химические изменения объема и на изменения разделяющих давлений, действующих через затрудненные слои адсорбированной воды в нанопорах (которые в среднем имеют толщину <1 нм и не более 10 молекул воды, или 2,7 нм , толщиной), заключенный между листами CSH. Расклинивающие давления сначала развиваются из-за неравномерного изменения объема продуктов гидратации, а затем релаксируют из-за ползучести в CSH, чтобы поддерживать термодинамическое равновесие (т. Е. Равенство химических потенциалов воды) с водяным паром в порах капилляров, и нарастают из-за любых изменений температуры или влажности в этих порах. Скорость разрывов связи можно считать квадратичной функцией уровня микронапряжений, для чего требуется уравнение. (4) можно обобщить как

${ displaystyle 1 / eta _ {f} = q_ {4} S}$

(5)

Важным свойством является то, что приложенная нагрузка не оказывает заметного влияния на микроперепряжение (поскольку поровая вода намного более сжимаема, чем твердый каркас, и ведет себя как мягкая пружина, соединенная параллельно с жестким каркасом). Микронапряжение со временем спадает, и его эволюция в каждой точке конкретной конструкции может быть решена с помощью дифференциального уравнения

${ displaystyle { dot {S}} + c_ {0} S ^ {2} = c_ {1} left | { dot {T}} ln h + T { dot {h}} / h право |}$

(6)

где ${ displaystyle c_ {0}, c_ {1}}$ = положительные константы (абсолютное значение гарантирует, что ${ displaystyle S}$ никогда не может стать отрицательным). Микропресса может моделировать тот факт, что сушка и охлаждение, а также смачивание и нагревание ускоряют ползучесть. Тот факт, что изменения ${ displaystyle w}$ или ${ displaystyle h}$ создают новые пики микроперепряжения и тем самым активируют новые участки ползучести, что объясняет эффект ползучести при высыхании. Частично этот эффект, однако, вызван тем фактом, что микротрещины в сопутствующем образце без нагрузки делают его общую усадку меньше, чем усадка в образце без трещин (сжатый), тем самым увеличивая разницу между ними (что и определяет ползать).

Понятие микропресса также необходимо для объяснения жесткости, вызванной старением. Одной из физических причин старения является то, что продукты гидратации постепенно заполняют поры затвердевшего цементного теста, что отражается в функции${ Displaystyle v (т)}$ в уравнении. (3). Но гидратация прекращается примерно через год, но эффект возраста при нагрузке ${ displaystyle t '}$ сильна даже по прошествии многих лет. Объяснение заключается в том, что пики микронапряжений с возрастом ослабляются, что снижает количество участков ползучести и, следовательно, скорость разрывов связей.

В переменной среде время ${ displaystyle t}$ в уравнении. (3) необходимо заменить на эквивалентное время гидратации ${ displaystyle t_ {e} = int beta _ {h} beta _ {T} { mbox {d}} t}$ где ${ displaystyle beta _ {h}}$ = убывающая функция ${ displaystyle h}$ (0, если ${ displaystyle h <}$ около 0,8) и ${ displaystyle beta _ {h} propto { mbox {e}} ^ {- Q_ {h} T / R}}$ ${ displaystyle (Q_ {h} / R приблизительно { mbox {2700 K}})}$. В уравнении. (4), ${ Displaystyle theta = т-т '}$ должен быть заменен на ${ displaystyle t_ {r} -t '_ {r}}$ где ${ displaystyle t_ {r} = int psi _ {h} psi _ {T} { mbox {d}} t}$ = сокращенное время (или срок погашения), улавливая эффект ${ displaystyle h}$ и ${ displaystyle T}$ по вязкости ползучести; ${ displaystyle psi _ {h}}$ = функция ${ displaystyle h}$ уменьшается с 1 на ${ displaystyle h = 1}$ до 0 в ${ displaystyle h = 0}$; ${ displaystyle psi _ {T} propto { mbox {e}} ^ {- Q_ {v} T / R}}$, ${ Displaystyle Q_ {v} / R приблизительно}$ 5000 К.

Эволюция профилей влажности ${ Displaystyle ч ( mathbf {х}, т)}$ (${ displaystyle mathbf {x}}$ = вектор координат) можно приближенно рассматривать как не связанное с проблемой напряжения и деформации и может быть решено численно из уравнения диффузии ${ displaystyle { rm {{ dot {h}} =}}}$ div [${ displaystyle C (h)}$град ${ displaystyle h] + { dot {h}} _ {s} (t_ {e})}$} где ${ displaystyle h_ {s} (t_ {e})}$ = самовысыхание, вызванное гидратацией (которое достигает примерно 0,97 в обычных бетонах и примерно 0,80 в высокопрочных бетонах), ${ displaystyle C (h)}$ = коэффициент диффузии, который уменьшается примерно в 20 раз при ${ displaystyle h}$ снижается с 1,0 до 0,6. Скорость деформации свободной (неограниченной) усадки составляет примерно

${ displaystyle { dot { epsilon}} _ {sh} = k_ {sh} { dot {h}}}$

(7)

где ${ displaystyle k_ {sh}}$ = коэффициент усадки. Поскольку ${ displaystyle { dot { epsilon}} _ {sh}}$-значения в различных точках несовместимы, расчет общей усадки конструкций, а также испытательных образцов является проблемой анализа напряжений, в которой необходимо учитывать ползучесть и растрескивание.

Для структурного анализа методом конечных элементов с временными шагами полезно преобразовать основной закон в скоростную форму. Это может быть достигнуто путем приближения ${ Displaystyle C_ {g} ( theta)}$ с моделью цепочки Кельвина (или связанной функцией релаксации с моделью цепочки Максвелла). Интегралы истории, такие как уравнение. 1 затем исчезают из основного закона, а история характеризуется текущими значениями внутренних переменных состояния (частичные деформации или напряжения цепей Кельвина или Максвелла).

Преобразование в форму типа скорости также необходимо для введения эффекта переменной температуры, которая влияет (в соответствии с законом Аррениуса) как на вязкость цепей Кельвина, так и на скорость гидратации, что фиксируется${ displaystyle t_ {e}}$. Первый ускоряет ползучесть при повышении температуры, а второй замедляет ползучесть. Трехмерное тензорное обобщение уравнений. (3) - (7) требуется для конечно-элементного анализа конструкций.

Примерное поперечное сечение при сушке

Хотя в настоящее время возможны многомерные расчеты ползучести и влажной диффузии методом конечных элементов, упрощенный одномерный анализ бетонных балок или ферм, основанный на предположении о том, что плоские поперечные сечения остаются плоскими, все еще преобладает на практике. Хотя (в мостах с коробчатыми балками) это связано с ошибками прогиба порядка 30%. При таком подходе необходимо ввести среднюю функцию соответствия поперечного сечения ${ displaystyle { bar {J}} (т, т ', т_ {0})}$ (Рис. 1 внизу, кривые блеска) и функция средней усадки ${ displaystyle { bar { epsilon}} _ {ш} (т, т_ {0})}$ поперечного сечения (рис.1 слева и посередине) (${ displaystyle t_ {0}}$ = возраст на момент высыхания). По сравнению с точечным материальным уравнением алгебраические выражения для таких средних характеристик значительно сложнее и их точность ниже, особенно если поперечное сечение не подвергается центрическому сжатию. Следующие приближения были получены, и их коэффициенты оптимизированы путем подбора большой лабораторной базы данных для влажности окружающей среды. ${ displaystyle h_ {e}}$ ниже 98%:

${ displaystyle { bar { epsilon}} _ {sh} (t, t_ {0}) = - epsilon _ {sh infty} k_ {h} S (t), ~~~ k_ {h } = 1- {h_ {e}} ^ {3} ~~~~~}$

(8)

${ displaystyle S (t) = { mbox {tanh}} { sqrt { frac {t-t_ {0}} { tau _ {sh}}}}, ~~~ tau _ {sh} = k_ {t} (k_ {s} D) ^ {2} ~~~~~}$

(9)

где ${ displaystyle D = 2v / s}$ = эффективная толщина, ${ displaystyle v / s}$ = отношение объема к поверхности, ${ displaystyle k_ {t}}$ = 1 для нормального цемента (тип I); ${ displaystyle k_ {s}}$ = коэффициент формы (например, 1,0 для плиты, 1,15 для цилиндра); и ${ displaystyle epsilon _ {ш infty} приблизительно epsilon _ {s infty} E (607) / (E (t_ {0} + tau _ {sh})}$, ${ displaystyle epsilon _ {s infty}}$ = константа; ${ displaystyle E (t) приблизительно E (28) { sqrt {4 + 0.85t}}}$ (все время в днях). Уравнения. (3) и (4) применяются, за исключением того, что ${ displaystyle 1 / eta _ {f}}$ должен быть заменен на

${ displaystyle { frac {1} {{ bar { eta}} _ {f}}} = { frac {q_ {4}} {t}} + q_ {5} { frac { partial} { partial t}} { sqrt {F (t) -F (t '_ {0})}}}$

(10)

где ${ Displaystyle F (T) = ехр {- 8 [1- (1-h_ {e}) S (t)] }}$ и ${ displaystyle t '_ {0} = max (t', t_ {0})}$. Форма выражения для полупериода усадки ${ Displaystyle тау _ {ш}}$ основан на теории диффузии. Функция tanh в уравнении. 8 - простейшая функция, удовлетворяющая двум асимптотическим условиям, вытекающим из теории диффузии: 1) для коротких времен ${ displaystyle { bar { epsilon}} _ {sh} propto { sqrt {t-t_ {0}}}}$и 2) к окончательной усадке следует приближаться экспоненциально. Существуют и обобщения для температурного эффекта.

Эмпирические формулы были разработаны для прогнозирования значений параметров в приведенных выше уравнениях на основе прочности бетона и некоторых параметров бетонной смеси. Однако они очень грубые, что приводит к ошибкам прогноза с коэффициентами вариации около 23% для ползучести и 34% для усадки при высыхании. Эти высокие неопределенности могут быть значительно уменьшены путем обновления некоторых коэффициентов формул в соответствии с кратковременными испытаниями на ползучесть и усадку данного бетона. Однако для усадки необходимо также измерить потерю веса образцов для испытаний на высыхание (иначе возникнет проблема обновления ${ displaystyle epsilon _ {ш infty}}$ в плохом состоянии). Полностью рациональное предсказание свойств бетона на ползучесть и усадку на основе его состава - сложная проблема, далеко не решенная удовлетворительно.

Инженерные приложения

Вышеупомянутая форма функций ${ Displaystyle J (т, т ')}$ и ${ Displaystyle epsilon _ {ш} (т)}$ был использован при проектировании конструкций с высокой чувствительностью к ползучести.Другие формы были введены в нормы проектирования и стандартные рекомендации инженерных обществ. Они проще, но менее реалистичны, особенно для многолетней ползучести.

Ползучесть и усадка могут вызвать серьезную потерю предварительного напряжения. Недооценка многолетней ползучести вызвала чрезмерные прогибы, часто с трещинами, во многих предварительно напряженных сегментно возводимых мостах с коробчатыми балками с большим пролетом (задокументировано более 60 случаев). Ползучесть может вызвать чрезмерное напряжение и растрескивание вантовых или арочных мостов, а также кровельных покрытий. Неравномерность ползучести и усадки, вызванная различиями в истории влажности и температуры пор, возраста и типа бетона в различных частях конструкции, может привести к растрескиванию. Так могут взаимодействовать с кладкой или стальными деталями, как в вантовых мостах и ​​композитных железобетонных балках. Различия в укорочении колонн особенно важны для очень высоких зданий. В тонких конструкциях ползучесть может вызвать обрушение из-за длительной нестабильности.

Эффекты ползучести особенно важны для предварительно напряженных бетонных конструкций (из-за их гибкости и гибкости) и имеют первостепенное значение при анализе безопасности защитных кожухов и корпусов ядерных реакторов. главная роль.

При предварительном проектировании конструкций в упрощенных расчетах удобно использовать безразмерный коэффициент ползучести ${ Displaystyle varphi (т, т ') = Е (т') J (т, т ') - 1}$ = ${ displaystyle epsilon _ { mbox {creep}} / epsilon _ { mbox {начальный}}}$. Изменение состояния структуры от времени ${ displaystyle t_ {1}}$ начальной загрузки во время ${ displaystyle t}$ можно просто, хотя и грубо, оценить с помощью квазиупругого анализа, в котором модуль Юнга ${ displaystyle E}$ заменяется так называемым эффективным модулем упругости с поправкой на возраст ${ displaystyle E '' (t, t_ {1}) = [E (t_ {1}) - R (t, t_ {1})] / varphi (t, t_ {1})}$.

Наилучший подход к компьютерному анализу ползучести чувствительных структур - преобразование закона ползучести в соотношение возрастающих упругих напряжений и деформаций с собственное напряжение. Уравнение (1) можно использовать, но в этой форме нельзя вводить изменения влажности и температуры со временем, и необходимость хранить всю историю напряжений для каждого конечного элемента является громоздкой. Лучше преобразовать уравнение. (1) к системе дифференциальных уравнений, основанной на реологической модели цепочки Кельвина. С этой целью характеристики ползучести на каждом достаточно малом временном шаге можно рассматривать как нестареющие, и в этом случае непрерывный спектр модулей замедления цепи Кельвина может быть получен из ${ Displaystyle J (т, т ')}$ по явной формуле Виддера для приближенного обращения преобразования Лапласа. Модули ${ Displaystyle E_ {k} (т)}$ (${ displaystyle k = 1,2, ... n_ {E}}$) единиц Кельвина затем дискретизируют этот спектр. Они различны для каждой точки интегрирования каждого конечного элемента на каждом временном шаге. Таким образом, задача анализа ползучести преобразуется в серию анализов упругих конструкций, каждый из которых может быть выполнен в коммерческой программе конечных элементов. Для примера см. Последнюю ссылку ниже.

Избранная библиография

использованная литература