Волоконная дифракция - Fiber diffraction

Волоконная дифракция является частью рассеяние, область, в которой молекулярная структура определяется по данным рассеяния (обычно рентгеновских лучей, электронов или нейтронов). При дифракции волокна картина рассеяния не изменяется, поскольку образец вращается вокруг единственной оси (оси волокна). Такая одноосная симметрия часто встречается у нитей или волокон, состоящих из биологических или искусственных материалов. макромолекулы. В кристаллография Симметрия волокна затрудняет определение кристаллической структуры, потому что отражения размываются и могут перекрываться в дифракционной картине волокна. Материаловедение рассматривает симметрию волокна как упрощение, поскольку почти вся доступная структурная информация содержится в одном двухмерный (2D) дифракционная картина, экспонированная на фотопленке или на 2D-детекторе. 2 вместо 3-х координатных направлений достаточно для описания дифракции волокна.

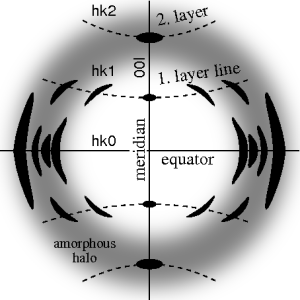
Идеальная дифракционная картина волокна от полукристаллического материала с аморфным ореолом и отражениями на линиях слоев. Высокая интенсивность представлена ​​темным цветом. Ось волокна вертикальная

Идеальная структура волокон демонстрирует 4-квадрантная симметрия. В идеальной схеме ось волокна называется меридианперпендикулярное направление называется экватор. В случае симметрии волокна на 2D-картине появляется намного больше отражений, чем при дифракции на монокристалле. На рисунках волокон эти отражения четко расположены вдоль линий (линии слоя) идущий почти параллельно экватору. Таким образом, в дифракции волокна понятие линии слоя кристаллография становится ощутимым. Линии загнутого слоя говорят о том, что узор необходимо расправить. Отражения отмечены значком Индекс Миллера hkl, т.е. 3 цифры. Размышления о ядоля линии -го слоя l =я. Отражения на меридиане - это 001-отражения. В кристаллография Дифракционные картины искусственного волокна генерируются путем вращения монокристалла вокруг оси (метод вращающегося кристалла).

Экспериментально получены неидеальные рисунки волокон. Они показывают только зеркальную симметрию относительно меридиана. Причина в том, что ось волокна и падающий луч (рентгеновские лучи, электроны, нейтроны) не могут быть точно ориентированы перпендикулярно друг другу. Соответствующее геометрическое искажение широко изучалось Майкл Поланьи введение концепции Сфера Поланьи (Немецкий: «Лагенкугель») пересекающиеся Сфера Эвальда. Потом Розалинд Франклин и Раймонд Гослинг провели собственное геометрическое рассуждение и представили приближенное уравнение для угла наклона волокна β. Анализ начинается с отображения искаженного 2D-рисунка на репрезентативной плоскости волокна. Это плоскость, которая содержит ось цилиндра в взаимное пространство. В кристаллография сначала приближение отображения в взаимное пространство вычисляется, которое уточняется итеративно. Цифровой метод, который часто называют Поправка Фрейзера начинается с приближения Франклина для угла наклона β. Он устраняет наклон волокна, устраняет искажение изображения детектора и корректирует интенсивность рассеяния. Правильное уравнение для определения β было представлено Норбертом Стрибеком.

Историческая роль

Волокнистые материалы, такие как шерсть или хлопок, легко образуют выровненные пучки и были одними из первых биологических макромолекул, исследованных методом дифракции рентгеновских лучей, в частности Уильям Эстбери в начале 1930-х гг. Данные дифракции волокна привели к нескольким важным достижениям в разработке структурная биология, например, оригинальные модели α-спираль и модель Уотсона-Крика двухцепочечной ДНК.

Геометрия дифракции волокна

Геометрия дифракции волокна изменяется при наклоне волокна (угол наклона β находится между синей жесткой осью и осью, обозначенной s-пространство). Информация о структуре находится в обратном пространстве (черные оси), растянутом на поверхности сфер Поланьи. В анимации отслеживается 1 сфера Поланьи с 1 отражением на ней.

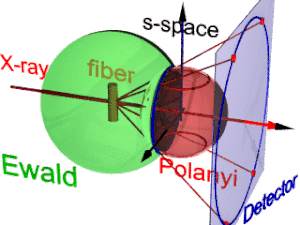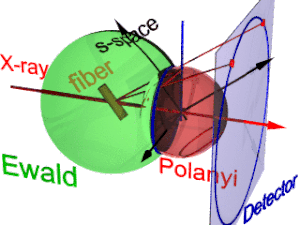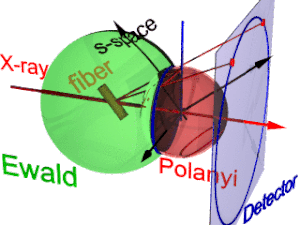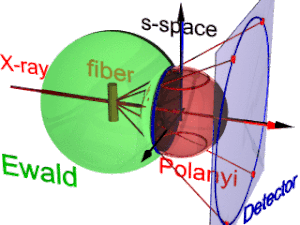
Анимация показывает геометрию дифракции волокна. Он основан на идеях, предложенных Поланьи. Ссылочное направление первичного пучка (этикетки: рентгеновская). Если волокно отклонено от перпендикулярного направления на угол β, то также информация о его молекулярной структуре в обратном пространстве (трехгранник, помеченный s-пространство) наклонен. В обратном пространстве Сфера Эвальда центр находится в образце. Его радиус равен 1 / λ, а λ - длина волны падающего излучения. На поверхности Сфера Эвальда найдены все точки обратного пространства, видимые детектором. Эти точки нанесены на пиксели детектора центральной проекцией.

В s-пространстве каждое отражение находится на своей сфере Поляни. По сути, идеальное отражение - это точка в s-пространстве, но симметрия волокна превращает ее в кольцо, размазанное при вращении вокруг направления волокна. Два кольца представляют каждое отражение на сфере Поляни, потому что рассеяние точечно симметричный относительно происхождения s-пространства. На детектор отображаются только те точки отражения в s-пространстве, которые обе находятся на Сфера Эвальда и на Сфера поланьи. Эти точки образуют круг отражения (синее кольцо). Он не меняется при наклоне волокна. Как и в случае с диапроектором, на детектор проецируется круг отражения (движущиеся красные лучи) (детектор круг, синее кольцо). Может появиться до 4 изображений (красных пятен) наблюдаемого отражения. Положение отраженных изображений является функцией ориентации волокна в первичном пучке (Уравнение поланьи). В инвертированном виде по положениям отраженных изображений можно определить ориентацию волокна, если для Индекс Миллера ${displaystyle hkl}$ обе ${displaystyle | h | + | k | eq 0}$ и ${displaystyle leq 0}$ действует. Из представления Поланьи о геометрии дифракции волокна соотношения отображения волокна устанавливаются формулой элементарный и сферическая геометрия.

Коррекция рисунка

Измеренный рисунок волокон

Структура волокна полипропилен отображается в (репрезентативную плоскость) обратное пространство

На рисунке слева показан типичный рисунок волокон полипропилен перед отображением его в обратном пространстве. Ось зеркала в шаблоне повернута на угол ${displaystyle ~ phi}$ относительно вертикального направления. Этот недостаток компенсируется простым поворотом картинки. 4 прямые стрелки указывают на 4 изображения отражения выбранного эталонного отражения. Их положение используется для определения угла наклона волокна. ${displaystyle eta}$. Изображение было записано на детектор CCD. Он показывает логарифмическую интенсивность в псевдоцветном представлении. Здесь яркие цвета представляют высокую интенсивность.

После определения ${displaystyle eta}$ расстояние между образцом и детектором вычисляется с использованием известных кристаллографических данных эталонного отражения, строится карта с равномерной сеткой для репрезентативной плоскости волокна в обратном пространстве, и данные дифракции вводятся в эту карту. На рисунке справа показан результат. Учтено изменение интенсивности рассеяния в процессе деформации. Из-за кривизны поверхности Сфера Эвальда на меридиане остаются белые пятна, в которых отсутствует структурная информация. Только в центре изображения и при значении s, связанном с углом рассеяния. ${displaystyle 2 eta}$ есть структурная информация на меридиане. Конечно, теперь есть 4-квадрантная симметрия. Это означает, что в примере шаблона часть недостающей информации может быть скопирована «из нижней половины в верхнюю» в белые области. Таким образом, часто имеет смысл намеренно наклонить волокно.

Трехмерное представление обратного пространства, заполненного данными рассеяния от полипропиленового волокна

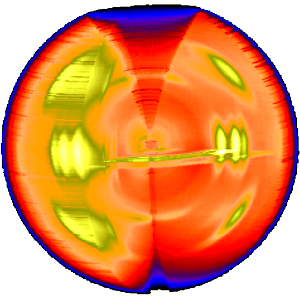
Трехмерный эскиз демонстрирует, что в примере эксперимента собранная информация о молекулярной структуре полипропиленового волокна почти полная. При вращении плоского рисунка вокруг меридиана данные рассеяния, собранные за 4 с, заполняют почти сферический объем s-пространства. В этом примере 4-квадрантная симметрия еще не учитывалась для заполнения части белых пятен. Для наглядности вырезана четверть сферы, но сохранена сама экваториальная плоскость.

Рекомендации

• Арнотт С. и Вонакотт А. Дж. Уточнение молекулярных и кристаллических структур полимеров с использованием данных рентгеновского излучения и стереохимических ограничений, Полимер, 1966 г. 7 157 - 166
• Биан В., Ван Х, Маккалло И., Стаббс Г. (2006). «WCEN: компьютерная программа для первичной обработки дифрактограмм волокна». J. Appl. Cryst., 39, 752-756.
• Банн С. В., Химическая кристаллография, Оксфордский университет, 2-е изд., 1967
• Кэмпбелл Смит П. Дж. И Арнотт С., LALS (и др.) Acta Crystallogr 1978 A34 3 - 11
• Кокран В., Крик ФХК и Ванд В. (1952). «Строение синтетических полипептидов. I. Преобразование атомов по спирали». Acta Crystallogr., 5, 581-586.
• Донохью Дж., Трублад К. Н., О ненадежности индекса надежности, Acta Crystallogr, 1956, 9, 615
• Франклин Р.Э., Гослинг Р.Г. (1953) "Структура тимонуклеатных волокон натрия. II. Цилиндрически симметричная функция Паттерсона". Acta Crystallogr., 6, 678-685
• Fraser RDB, Macrae TP, Miller A, Rowlands RJ (1976). «Цифровая обработка дифрактограмм волокна». J. Appl. Cryst., 9, 81-94.
• Гамильтон В. С., R-факторы, статистика и правда, статья H5, Amer Cryst Ass Program & Abstracts, Боулдер, Колорадо, 1961 г.
• Гамильтон В. К., Тесты значимости кристаллографического фактора R, Acta Crystallogr, 1965. 18 502 - 510
• Джеймс Т. В. и Мазиа Д., Поверхностные пленки дезоксирибонуклеиновой кислоты, Biochim Biophys Acta 1953 10 367 - 370
• Марвин Д.А. (2017) «Волоконно-дифракционные исследования биологических макромолекул». Прог. Биофиз. Мол. Биол. 127, 43-87.
• Миллейн Р.П., Арнотт С. (1985) "Цифровая обработка картин дифракции рентгеновских лучей от ориентированных волокон". J. Macromol. Sci. Phys., B24, 193-227
• Polanyi M (1921) "Das Röntgen-Faserdiagramm (Erste Mitteilung)". Z. Physik, 7, 149-180
• Polanyi M, Weissenberg K (1923) "Das Röntgen-Faserdiagramm (Zweite Mitteilung)". Z. Physik, 9, 123-130
• Rajkumar G, AL-Khayat H, Eakins F, He A, Knupp C, Squire J (2005) «FibreFix - новый интегрированный программный пакет CCP13», Fiber Diffraction Rev., 13, 11-18
• Стрибек Н. (2009). «Об определении углов наклона волокна при дифракции волокна» Acta Crystallogr., A65, 46-47

Учебники

• Александр LE (1979) "Методы дифракции рентгеновских лучей в науке о полимерах", Wiley, Нью-Йорк
• Klug HP, Alexander LE (1974) "Процедуры дифракции рентгеновских лучей для поликристаллических и аморфных материалов", 2-е изд., Wiley, New York
• Уоррен Б.Е. (1990) «Рентгеновская дифракция». Дувр, Нью-Йорк
• Саад Мохамед (1994) «Исследование структуры и упаковки кристаллических доменов коллагена в сухожилиях с низким разрешением с использованием рентгеновских лучей синхротронного излучения, определение структурных факторов, оценка методов изоморфного замещения и другое моделирование». Кандидатская диссертация, Университет Жозефа Фурье, Гренобль 1

внешняя ссылка

• WCEN - Программное обеспечение (Linux, Mac, Windows) для анализа структуры волокон
• Волоконная дифракция - введение, предоставленное профессором К. Холмс, Институт медицинских исследований Макса Планка, Гейдельберг.