Кригинг с усилением градиента - Gradient-enhanced kriging

Кригинг с усилением градиента (GEK) это суррогатное моделирование техника, применяемая в машиностроении. Суррогатная модель (также известная как метамодель, поверхность отклика или эмулятор) - это предсказание вывода дорогостоящего компьютерного кода.^[1] Этот прогноз основан на небольшом количестве оценок дорогостоящего компьютерного кода.

Введение

Пример одномерных данных, интерполированных Кригингом и GEK. Черная линия обозначает тестовую функцию, а серые кружки обозначают «наблюдения», «образцы» или «оценки» тестовой функции. Синяя линия - это среднее значение Кригинга, заштрихованная синяя область - стандартное отклонение Кригинга. С помощью GEK мы можем добавить информацию о градиенте, показанную красным, что увеличивает точность прогноза.

Сопряженные решатели теперь становятся доступными в ряде вычислительная гидродинамика (CFD) решатели, такие как Свободно, OpenFOAM, SU2 и US3D. Первоначально разработан для оптимизация, сопряженные решатели теперь все больше и больше используются в количественная оценка неопределенности.

Линейное ускорение

Сопряженный решатель позволяет вычислить градиент интересующего количества по всем параметрам конструкции за счет одного дополнительного решения. Это потенциально приводит к линейный ускорение: вычислительные затраты на построение точного суррогатного уменьшения и результирующее ускорение вычислений ${ displaystyle s}$ линейно масштабируется с числом ${ displaystyle d}$ проектных параметров.

Причина этого линейного ускорения проста. Предположим, мы бежим ${ displaystyle N}$ примал решает и ${ displaystyle N}$ сопряженные решает, общей стоимостью ${ displaystyle 2N}$ . Это приводит к ${ Displaystyle N + dN}$ данные; ${ displaystyle N}$ значения интересующего количества и ${ displaystyle d}$ частные производные в каждой из ${ displaystyle N}$ градиенты. Теперь предположим, что каждая частная производная предоставляет нашему суррогату столько же информации, сколько одно прямое решение. Тогда общая стоимость получения того же количества информации только от первичных решений равна ${ Displaystyle N + dN}$ . Ускорение - это соотношение этих затрат:^[2]^[3]

{ displaystyle s = { frac {N + dN} {2N}} = { frac {1} {2}} + { frac {1} {2}} d.}

Было продемонстрировано линейное ускорение для взаимодействие жидкости и конструкции проблема ^[2] и для трансзвуковой профиль.^[3]

Шум

Одна из проблем с сопряженными градиентами в CFD заключается в том, что они могут быть особенно шумный.^[4] ^[5] При выводе в Байесовский рамки, GEK позволяет включать не только информацию о градиенте, но и неуверенность в этой информации о градиенте.^[6]

Подход

При использовании GEK необходимо выполнить следующие действия:

Создайте план эксперимента (DoE): DoE или «план выборки» - это список различных мест в пространстве проектирования. DoE указывает, какие комбинации параметров будут использоваться для выборки компьютерного моделирования. При использовании Kriging и GEK обычным выбором является использование дизайна латинского гиперкуба (LHS) с критерием максимума. LHS-дизайн доступен в скриптовых кодах типа MATLAB или Python.
Сделайте наблюдения: Для каждого образца в нашем DoE запускается компьютерное моделирование, чтобы получить интересующее количество (QoI).
Постройте суррогат: Для построения суррогата, обусловленного полученными наблюдениями, используются уравнения-предикторы GEK.

После того, как суррогат создан, его можно использовать по-разному, например, для суррогатного материнства. количественная оценка неопределенности (UQ) или оптимизация.

Уравнения предикторов

В Байесовский рамки, мы используем Теорема Байеса предсказать Кригинг среднее значение и ковариация зависят от наблюдений. При использовании GEK наблюдения обычно являются результатами ряда компьютерных симуляций. ГЭК можно интерпретировать как форму Гауссовский процесс регресс.

Кригинг

По линиям, ^[7] нас интересует выход ${ displaystyle X}$ нашего компьютерного моделирования, для которого мы предполагаем нормальный априорное распределение вероятностей:

{ Displaystyle X sim { mathcal {N}} ( mu, P),}

с предварительным средним ${ displaystyle mu}$ и ранее ковариационная матрица ${ displaystyle P}$ . Наблюдения ${ displaystyle y}$ иметь нормальный вероятность:

{ displaystyle Y mid x sim { mathcal {N}} (Hx, R),}

с участием ${ displaystyle H}$ матрица наблюдения и ${ displaystyle R}$ ковариационная матрица ошибок наблюдения, содержащая неопределенности наблюдения. После применения Теорема Байеса получаем нормально распределенное апостериорное распределение вероятностей, со средним значением Кригинга:

{ Displaystyle OperatorName {E} (Икс середина у) = му + К (у-Н му),}

и ковариация Кригинга:

{ displaystyle operatorname {cov} (X mid y) = (I-KH) P,}

где у нас есть матрица усиления:

{ displaystyle K = PH ^ {T} (R + HPH ^ {T}) ^ {- 1}.}

В кригинге матрица априорной ковариации ${ displaystyle P}$ генерируется из ковариационной функции. Одним из примеров ковариационной функции является гауссовская ковариация:

{ Displaystyle P_ {ij} = sigma ^ {2} exp left (- sum _ {k} { frac {| xi _ {jk} - xi _ {ik} | ^ {2}} {2 theta _ {k} ^ {2}}} right),}

где мы суммируем по размерам ${ displaystyle k}$ и ${ Displaystyle xi}$ - входные параметры. В гиперпараметры ${ displaystyle mu}$ , ${ displaystyle sigma}$ и ${ displaystyle theta}$ можно оценить из Оценка максимального правдоподобия (MLE).^[6]^[8]

Косвенный GEK

Есть несколько способов реализации GEK. Первый метод, непрямой GEK, определяет небольшой, но конечный размер шага. ${ displaystyle h}$ , и использует информацию о градиенте для добавления синтетических данных к наблюдениям. ${ displaystyle y}$ см. например.^[8] Косвенный кригинг чувствителен к выбору размера шага ${ displaystyle h}$ и не может включать неопределенности наблюдения.

Прямой GEK (через априорную ковариационную матрицу)

Прямой GEK - это форма ко-кригинга, когда мы добавляем информацию о градиенте в качестве сопеременных. Это можно сделать, изменив предыдущую ковариацию ${ displaystyle P}$ или путем изменения матрицы наблюдения ${ displaystyle H}$ ; оба подхода приводят к одному и тому же предсказателю GEK. Когда мы строим прямой GEK через априорную ковариационную матрицу, мы добавляем частные производные к ${ displaystyle y}$ , и модифицируем априорную ковариационную матрицу ${ displaystyle P}$ так что он также содержит производные (и вторые производные) ковариационной функции, см., например, ^[9].^[6]Основными преимуществами прямого GEK перед непрямым GEK являются: 1) нам не нужно выбирать размер шага, 2) мы можем включить неопределенности наблюдения для градиентов в ${ displaystyle R}$ , и 3) он менее восприимчив к бедным кондиционирование матрицы усиления ${ displaystyle K}$ .^[6]^[8]

Прямой ГЭК (через матрицу наблюдения)

Другой способ получить тот же прямой предсказатель GEK - добавить частные производные к наблюдениям. ${ displaystyle y}$ и включать операторы частных производных в матрицу наблюдения ${ displaystyle H}$ см. например.^[10]

Кригинг с усилением градиента для задач большой размерности (косвенный метод)

Современные методы кригинга с улучшенным градиентом плохо масштабируются с количеством точек выборки из-за быстрого роста размера корреляционной матрицы, где новая информация добавляется для каждой точки выборки в каждом направлении пространства дизайна. Кроме того, они плохо масштабируются с количеством независимых переменных из-за увеличения количества гиперпараметров, которые необходимо оценить.Для решения этой проблемы был использован новый подход суррогатной модели с улучшенным градиентом, который резко сократил количество гиперпараметров за счет использование частичные наименьшие квадраты разработан метод, поддерживающий точность. Кроме того, этот метод может управлять размером корреляционной матрицы, добавляя только релевантные точки, определенные посредством информации, предоставленной методом частичных наименьших квадратов. Подробнее см.^[11]Этот подход реализован в Surrogate Modeling Toolbox (SMT) в Python (https://github.com/SMTorg/SMT ), и он работает в Linux, macOS и Windows. SMT распространяется под новой лицензией BSD.

Пример: коэффициент лобового сопротивления трансзвукового профиля

Трансзвуковой профиль.

Справочные результаты для коэффициента лобового сопротивления околозвукового профиля, основанные на большом количестве моделирования CFD. По горизонтальной и вертикальной осям показаны деформации формы профиля.

Кригинговая суррогатная модель коэффициента лобового сопротивления трансзвукового профиля. Серые точки обозначают конфигурации, для которых был запущен решатель CFD.

GEK суррогатная модель коэффициента лобового сопротивления трансзвукового профиля. Серые точки указывают конфигурации, для которых был запущен решатель CFD, стрелки указывают градиенты.

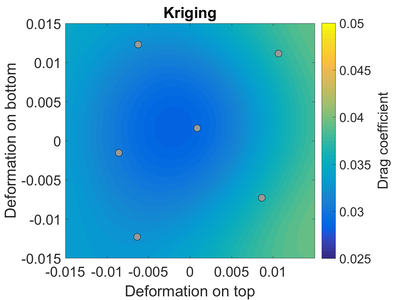
В качестве примера рассмотрим обтекание трансзвуковой профиль.^[3] Профиль работает на число Маха 0,8 и угол атаки 1,25 градуса. Мы предполагаем, что форма профиля не определена; верх и низ аэродинамического профиля могли сместиться вверх или вниз из-за производственных допусков. Другими словами, форма профиля, который мы используем, может немного отличаться от профиля, который мы разработали.

Справа мы видим эталонные результаты для коэффициент сопротивления профиля аэродинамического профиля на основе большого количества расчетов CFD. Обратите внимание, что наименьшее сопротивление, которое соответствует «оптимальным» характеристикам, близко к недеформированной «базовой» конструкции аэродинамического профиля в точке (0,0).

После разработки плана выборки (обозначенного серыми точками) и запуска решателя CFD в этих точках выборки мы получаем суррогатную модель Кригинга. Суррогат Кригинга близок к эталону, но, возможно, не так близок, как нам хотелось бы.

На последнем рисунке мы повысили точность этой суррогатной модели, включив информацию о сопряженном градиенте, указанную стрелками, и применив GEK.

Приложения

GEK нашла следующие применения:

1993: Задача проектирования для тестовой функции модели скважины.^[12]
2002: Аэродинамический дизайн сверхзвукового бизнес-джета.^[13]
2008: Количественная оценка неопределенности околозвукового профиля с неопределенными параметрами формы.^[9]
2009: Количественная оценка неопределенности околозвукового профиля с неопределенными параметрами формы.^[8]
2012: Построение суррогатной модели для проблемы расхождения панелей, взаимодействие жидкости и конструкции проблема. Демонстрация линейного ускорения.^[2]
2013: Количественная оценка неопределенности околозвукового профиля с неопределенным углом атаки и числом Маха.^[14]
2014: Количественная оценка неопределенности для RANS-моделирования аэродинамического профиля с параметрами модели k-эпсилон-модели турбулентности в качестве неопределенных входных данных.^[6]
2015: Количественная оценка неопределенности для моделирования Эйлера трансзвукового крылового профиля с неопределенными параметрами формы. Демонстрация линейного ускорения.^[3]
2016: Построение суррогатной модели на двоих взаимодействие жидкости и конструкции проблемы.^[15]
2017: Большой обзор суррогатных моделей с градиентным усилением, включая множество деталей, касающихся градиентного кригинга.^[16]
2017: Распространение неопределенности для ядерной энергетической системы.^[17]
2020: Оптимизация геометрии молекул.^[18]

использованная литература

^ Mitchell, M .; Моррис, М. (1992). «Байесовский дизайн и анализ компьютерных экспериментов: два примера» (PDF). Statistica Sinica (2): 359–379.
^ ^а ^б ^c де Баар, J.H.S .; Scholcz, T.P .; Verhoosel, C.V .; Dwight, R.P .; van Zuijlen, A.H .; Бейл, Х. (2012). «Эффективная количественная оценка неопределенности с помощью градиентного кригинга: приложения в FSI» (PDF). ЭККОМАС, Вена, Австрия, 10–14 сентября..
^ ^а ^б ^c ^d де Баар, J.H.S .; Scholcz, T.P .; Дуайт, Р.П. (2015). «Использование сопряженных производных в многомерных метамоделях». Журнал AIAA. 53 (5): 1391–1395. Bibcode:2015AIAAJ..53.1391D. Дои:10.2514 / 1.J053678.
^ Dwight, R .; Брезильон, Дж. (2006). «Влияние приближений дискретного сопряжения на градиентную оптимизацию». Журнал AIAA. 44 (12): 3022–3031. Bibcode:2006AIAAJ..44.3022D. CiteSeerX 10.1.1.711.4761. Дои:10.2514/1.21744.
^ Giles, M .; Дута, М .; Muller, J .; Пирс, Н. (2003). «Разработка алгоритмов для дискретных сопряженных методов». Журнал AIAA. 41 (2): 198–205. Bibcode:2003AIAAJ..41..198G. Дои:10.2514/2.1961. S2CID 2106397.
^ ^а ^б ^c ^d ^е де Баар, J.H.S .; Dwight, R.P .; Биджл, Х. (2014). «Улучшения градиентного кригинга с использованием байесовской интерпретации». Международный журнал количественной оценки неопределенности. 4 (3): 205–223. Дои:10.1615 / Int.J.UncertaintyQuantification.2013006809.
^ Wikle, C.K .; Берлинер, Л. М. (2007). «Байесовское руководство по усвоению данных». Physica D. 230 (1–2): 1–16. Bibcode:2007PhyD..230 .... 1Вт. Дои:10.1016 / j.physd.2006.09.017.
^ ^а ^б ^c ^d Dwight, R.P .; Хан, З.-Х. (2009). Эффективная количественная оценка неопределенности с использованием градиентного кригинга (PDF). 11-я конференция AIAA по недетерминированным подходам, Палм-Спрингс, Калифорния, 4–7 мая. Дои:10.2514/6.2009-2276. ISBN 978-1-60086-975-4.
^ ^а ^б Laurenceau, J .; Сагаут, П. (2008). «Построение эффективных поверхностей отклика аэродинамических функций с помощью кригинга и кокригинга». Журнал AIAA. 46 (2): 498–507. Bibcode:2008AIAAJ..46..498L. Дои:10.2514/1.32308. S2CID 17895486.
^ де Баар, J.H.S. (2014). «Стохастические суррогаты для измерений и компьютерных моделей жидкостей». Докторская диссертация, Делфтский технологический университет: 99–101.
^ Bouhlel, M.A .; Мартинс, J.R.R.A. (2018). «Градиентный кригинг для задач большой размерности». Разработка с помощью компьютеров. 35: 157–173. arXiv:1708.02663. Дои:10.1007 / s00366-018-0590-х.
^ Моррис, доктор медицины; Mitchell, T.J .; Илвисакер, Д. (1993). «Байесовский дизайн и анализ компьютерных экспериментов: использование производных в предсказании поверхности». Технометрика. 35 (3): 243–255. Дои:10.1080/00401706.1993.10485320.
^ Chung, H.-S .; Алонсо, Дж. Дж. (2002). «Использование градиентов для построения моделей аппроксимации кокригинга для задач оптимизации проекта большой размерности». 40-е собрание и выставка AIAA по аэрокосмическим наукам: 2002–0317. CiteSeerX 10.1.1.12.4149. Дои:10.2514/6.2002-317.
^ Han, Z.-H .; Горц, С .; Циммерманн, Р. (2013). «Улучшение суррогатного моделирования с переменной точностью с помощью градиентного кригинга и обобщенной гибридной функции моста». Разработка с помощью компьютеров. 32 (1): 15–34. Дои:10.1016 / j.ast.2012.01.006.
^ Ulaganathan, S .; Couckuyt, I .; Dhaene, T .; Degroote, J .; Лаерманс, Э. (2016). "Исследование эффективности градиентного кригинга". Аэрокосмическая наука и технологии. 25 (1): 177–189.
^ Laurent, L .; Le Riche, R .; Soulier, B .; Букар, П.-А. (2017). «Обзор метамоделей с улучшенными градиентами и приложениями» (PDF). Архивы вычислительных методов в технике. 26: 1–46. Дои:10.1007 / s11831-017-9226-3.
^ Lockwood, B.A .; Анитеску, М. (2012). «Универсальный кригинг с градиентным усилением для распространения неопределенности» (PDF). Ядерная наука и инженерия. 170 (2): 168–195. CiteSeerX 10.1.1.187.6097. Дои:10.13182 / NSE10-86.
^ Raggi, G .; Фдез. Galván, I .; Ritterhoff, C.L .; Вашер, М .; Линд, Р. (2020). «Оптимизация молекулярной геометрии с ограниченными отклонениями на основе градиентно-усиленного кригинга». Журнал химической теории и вычислений. 16 (6): 3989–4001. Дои:10.1021 / acs.jctc.0c00257. PMID 32374164.

[mitchell1992-1] Mitchell, M .; Моррис, М. (1992). «Байесовский дизайн и анализ компьютерных экспериментов: два примера» (PDF). Statistica Sinica (2): 359–379.

[debaar2012-2] а ^б ^c де Баар, J.H.S .; Scholcz, T.P .; Verhoosel, C.V .; Dwight, R.P .; van Zuijlen, A.H .; Бейл, Х. (2012). «Эффективная количественная оценка неопределенности с помощью градиентного кригинга: приложения в FSI» (PDF). ЭККОМАС, Вена, Австрия, 10–14 сентября..

[debaar2015-3] а ^б ^c ^d де Баар, J.H.S .; Scholcz, T.P .; Дуайт, Р.П. (2015). «Использование сопряженных производных в многомерных метамоделях». Журнал AIAA. 53 (5): 1391–1395. Bibcode:2015AIAAJ..53.1391D. Дои:10.2514 / 1.J053678.

[dwight2006-4] Dwight, R .; Брезильон, Дж. (2006). «Влияние приближений дискретного сопряжения на градиентную оптимизацию». Журнал AIAA. 44 (12): 3022–3031. Bibcode:2006AIAAJ..44.3022D. CiteSeerX 10.1.1.711.4761. Дои:10.2514/1.21744.

[giles2003-5] Giles, M .; Дута, М .; Muller, J .; Пирс, Н. (2003). «Разработка алгоритмов для дискретных сопряженных методов». Журнал AIAA. 41 (2): 198–205. Bibcode:2003AIAAJ..41..198G. Дои:10.2514/2.1961. S2CID 2106397.

[debaar2014a-6] а ^б ^c ^d ^е де Баар, J.H.S .; Dwight, R.P .; Биджл, Х. (2014). «Улучшения градиентного кригинга с использованием байесовской интерпретации». Международный журнал количественной оценки неопределенности. 4 (3): 205–223. Дои:10.1615 / Int.J.UncertaintyQuantification.2013006809.

[7] Wikle, C.K .; Берлинер, Л. М. (2007). «Байесовское руководство по усвоению данных». Physica D. 230 (1–2): 1–16. Bibcode:2007PhyD..230 .... 1Вт. Дои:10.1016 / j.physd.2006.09.017.

[dwight2009-8] а ^б ^c ^d Dwight, R.P .; Хан, З.-Х. (2009). Эффективная количественная оценка неопределенности с использованием градиентного кригинга (PDF). 11-я конференция AIAA по недетерминированным подходам, Палм-Спрингс, Калифорния, 4–7 мая. Дои:10.2514/6.2009-2276. ISBN 978-1-60086-975-4.

[laurenceau2008-9] а ^б Laurenceau, J .; Сагаут, П. (2008). «Построение эффективных поверхностей отклика аэродинамических функций с помощью кригинга и кокригинга». Журнал AIAA. 46 (2): 498–507. Bibcode:2008AIAAJ..46..498L. Дои:10.2514/1.32308. S2CID 17895486.

[10] де Баар, J.H.S. (2014). «Стохастические суррогаты для измерений и компьютерных моделей жидкостей». Докторская диссертация, Делфтский технологический университет: 99–101.

[bouhlel2018-11] Bouhlel, M.A .; Мартинс, J.R.R.A. (2018). «Градиентный кригинг для задач большой размерности». Разработка с помощью компьютеров. 35: 157–173. arXiv:1708.02663. Дои:10.1007 / s00366-018-0590-х.

[morris1993-12] Моррис, доктор медицины; Mitchell, T.J .; Илвисакер, Д. (1993). «Байесовский дизайн и анализ компьютерных экспериментов: использование производных в предсказании поверхности». Технометрика. 35 (3): 243–255. Дои:10.1080/00401706.1993.10485320.

[chung2002-13] Chung, H.-S .; Алонсо, Дж. Дж. (2002). «Использование градиентов для построения моделей аппроксимации кокригинга для задач оптимизации проекта большой размерности». 40-е собрание и выставка AIAA по аэрокосмическим наукам: 2002–0317. CiteSeerX 10.1.1.12.4149. Дои:10.2514/6.2002-317.

[han2013-14] Han, Z.-H .; Горц, С .; Циммерманн, Р. (2013). «Улучшение суррогатного моделирования с переменной точностью с помощью градиентного кригинга и обобщенной гибридной функции моста». Разработка с помощью компьютеров. 32 (1): 15–34. Дои:10.1016 / j.ast.2012.01.006.

[ulaganathan2016-15] Ulaganathan, S .; Couckuyt, I .; Dhaene, T .; Degroote, J .; Лаерманс, Э. (2016). "Исследование эффективности градиентного кригинга". Аэрокосмическая наука и технологии. 25 (1): 177–189.

[laurent2017-16] Laurent, L .; Le Riche, R .; Soulier, B .; Букар, П.-А. (2017). «Обзор метамоделей с улучшенными градиентами и приложениями» (PDF). Архивы вычислительных методов в технике. 26: 1–46. Дои:10.1007 / s11831-017-9226-3.

[lockwood2010-17] Lockwood, B.A .; Анитеску, М. (2012). «Универсальный кригинг с градиентным усилением для распространения неопределенности» (PDF). Ядерная наука и инженерия. 170 (2): 168–195. CiteSeerX 10.1.1.187.6097. Дои:10.13182 / NSE10-86.

[Raggi2020-18] Raggi, G .; Фдез. Galván, I .; Ritterhoff, C.L .; Вашер, М .; Линд, Р. (2020). «Оптимизация молекулярной геометрии с ограниченными отклонениями на основе градиентно-усиленного кригинга». Журнал химической теории и вычислений. 16 (6): 3989–4001. Дои:10.1021 / acs.jctc.0c00257. PMID 32374164.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]