Координаты Гуллстранда – Пенлеве - Gullstrand–Painlevé coordinates

Координаты Гуллстранда – Пенлеве являются частным набором координат для Метрика Шварцшильда - решение Уравнения поля Эйнштейна который описывает черную дыру. Входящие координаты таковы, что координата времени следует за собственным временем свободно падающего наблюдателя, который стартует издалека с нулевой скоростью, а пространственные срезы являются плоскими. На радиусе Шварцшильда (горизонте событий) координатной сингулярности нет. Исходящие - это просто время, обратное входящим координатам (время - собственное время исходящих частиц, которые достигают бесконечности с нулевой скоростью).

Решение было предложено независимо Поль Пенлеве в 1921 г. ^[1] и Аллвар Гуллстранд^[2] в 1922 году. Он не был признан до 1933 года в Лемэтр бумага ^[3]что эти решения были просто координатными преобразованиями обычного решения Шварцшильда.

Вывод

Получение координат GP требует определения следующих систем координат и понимания того, как данные, измеренные для событий в одной системе координат, интерпретируются в другой системе координат.

Соглашение: все единицы измерения геометризованный. Время и масса измеряются в метрах. Скорость света в плоском пространстве-времени имеет значение 1. Гравитационная постоянная имеет значение 1. Метрика выражается в + −−− подписать соглашение.

Координаты Шварцшильда

Наблюдатель Шварцшильда - это дальний наблюдатель или бухгалтер. Он не измеряет напрямую события, происходящие в разных местах. Вместо этого он далеко от черной дыры и событий. Наблюдатели, участвующие в мероприятиях, привлекаются для проведения измерений и отправки ему результатов. Бухгалтер собирает и объединяет отчеты из разных мест. Числа в отчетах переводятся в данные в координатах Шварцшильда, которые обеспечивают систематические средства оценки и описания событий в глобальном масштабе. Таким образом, физик может разумно сравнивать и интерпретировать данные. Он может найти значимую информацию из этих данных. Форма Шварцшильда метрики Шварцшильда с использованием координат Шварцшильда дается выражением

{displaystyle g = left (1- {frac {2M} {r}} ight), dt ^ {2} - {frac {dr ^ {2}} {left (1- {frac {2M} {r}} ight) )}} - r ^ {2}, d heta ^ {2} -r ^ {2} sin ^ {2} heta, dphi ^ {2},}

куда

G = 1 = с

т, р, θ, φ - координаты Шварцшильда,

M это масса черной дыры.

Координаты GP

Определите новую временную координату с помощью

{displaystyle t_ {r} = t-a (r)}

для некоторой произвольной функции ${displaystyle a (r)}$ . Подставляя в метрику Шварцшильда, получаем

{displaystyle g = left (1- {frac {2M} {r}} ight), dt_ {r} ^ {2} + 2left (1- {frac {2M} {r}} ight), a'dt_ {r } dr-left ({frac {1} {1- {frac {2M} {r}}}} - left (1- {frac {2M} {r}} ight), {a '} ^ {2} ight ) dr ^ {2} -r ^ {2}, d heta ^ {2} -r ^ {2} sin ^ {2} heta, dphi ^ {2},}

куда ${displaystyle a '(r) = {frac {da} {dr}}}$ .Если мы сейчас выберем ${displaystyle a (r)}$ так что член умножения ${displaystyle dr ^ {2}}$ это единство, мы получаем

{displaystyle a '= - {frac {1} {1- {frac {2M} {r}}}} {sqrt {frac {2M} {r}}}}

и метрика становится

{displaystyle g = left (1- {frac {2M} {r}} ight), dt_ {r} ^ {2} -2 {sqrt {frac {2M} {r}}} dt_ {r} dr-dr ^ {2} -r ^ {2}, d heta ^ {2} -r ^ {2} sin ^ {2} heta, dphi ^ {2},}

Пространственная метрика (т.е. ограничение метрики ${displaystyle g | _ {t = t_ {r}}}$ на поверхности, где ${displaystyle t_ {r}}$ постоянна) - это просто плоская метрика, выраженная в сферических полярных координатах. Эта метрика регулярна вдоль горизонта, где r = 2M, поскольку, хотя временной член стремится к нулю, недиагональный член в метрике все еще не равен нулю и гарантирует, что метрика по-прежнему обратима (определитель метрики равен ${displaystyle -r ^ {4} sin (heta) ^ {2}}$ ).

Функция ${displaystyle a (r)}$ дан кем-то

{displaystyle a (r) = - int {frac {sqrt {frac {2M} {r}}} {1- {frac {2M} {r}}}} dr = 2Mleft (-2y + ln left ({frac { y + 1} {y-1}} ight) ight)}

куда ${displaystyle y = {sqrt {frac {r} {2M}}}}$ .Функция ${displaystyle a (r)}$ явно особенный в r = 2M как это должно быть, чтобы удалить эту особенность в метрике Шварцшильда.

Движение капли дождя

Определите каплю дождя как объект, который падает радиально в сторону черной дыры из состояния покоя на бесконечности. В координатах Шварцшильда скорость капли дождя определяется выражением

{displaystyle {frac {dr} {dt}} = - left (1- {frac {2M} {r}} ight) {sqrt {frac {2M} {r}}}.,}

Скорость стремится к 0 по мере приближения r к горизонту событий. Дождевая капля, кажется, замедлилась по мере приближения к горизонту событий и остановилась на горизонте событий, как измеряет бухгалтер. Действительно, наблюдатель за пределами горизонта событий увидел бы, что капля дождя падает все медленнее и медленнее. Его изображения бесконечно смещены в красную область и никогда не проходят через горизонт событий. Однако бухгалтер физически не измеряет скорость напрямую. Он переводит данные, передаваемые наблюдателем оболочки, в значения Шварцшильда и вычисляет скорость. В результате остается только бухгалтерская запись.

В координатах GP скорость определяется выражением

{displaystyle {frac {dr} {dt_ {r}}} = eta = - {sqrt {frac {2M} {r}}}.,}

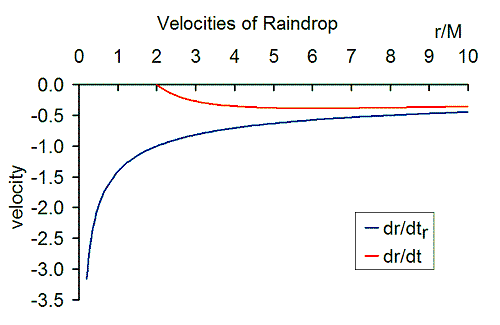
Скорость капли обратно пропорциональна квадратному корню из радиуса и равна отрицательному значению. ньютоновская скорость убегания. В местах, очень удаленных от черной дыры, скорость чрезвычайно мала. По мере того как капля дождя падает в сторону черной дыры, скорость увеличивается. На горизонте событий скорость имеет значение 1. На горизонте событий нет разрывов или сингулярностей.
Внутри горизонта событий ${displaystyle r <2M ,!}$ скорость увеличивается по мере приближения капли дождя к сингулярности. В конце концов, в сингулярности скорость становится бесконечной. Как показано ниже, скорость всегда меньше скорости света. Результаты могут быть неверно предсказаны уравнением в точке и очень близко к сингулярности, поскольку истинное решение может быть совершенно другим, если включить квантовую механику.
Несмотря на проблему с сингулярностью, все еще возможно вычислить время прохождения капли дождя от горизонта до центра черной дыры математически.

Интегрируем уравнение движения:

{displaystyle int _ {0} ^ {T_ {r}}, dt = -int _ {2M} ^ {0} left ({sqrt {frac {2M} {r}}} ight) ^ {- 1}, dr .,}

Результат

{displaystyle T_ {r} = {frac {4} {3}} M.,}

Используя этот результат для скорости капли дождя, мы можем найти собственное время вдоль траектории капли в терминах времени ${displaystyle t_ {r}}$ . У нас есть

{displaystyle d au ^ {2} = g | _ {ext {trajectory}} = dt_ {r} ^ {2} left [1- {frac {2M} {r}} + 2 {sqrt {frac {2M} { r}}} {sqrt {frac {2M} {r}}} - {sqrt {frac {2M} {r}}} ^ {2} ight] = dt_ {r} ^ {2}}

Т.е. по траектории капель дождя, по прошествии времени ${displaystyle t_ {r}}$ как раз собственное время по траектории. Можно было бы определить координаты GP по этому требованию, а не требуя, чтобы пространственные поверхности были плоскими.

Тесно связанным набором координат являются координаты Лемэтра, в которых «радиальная» координата выбрана постоянной вдоль траекторий дождевых капель. С р изменяется по мере падения капель дождя, этот показатель зависит от времени, а показатель GP не зависит от времени.

Метрика, полученная, если в приведенном выше примере взять функцию f (r) быть отрицательным по отношению к тому, что мы выбрали выше, также называется системой координат GP. Единственное изменение в метрике - изменение знака кросс-термина. Этот показатель является обычным для исходящих капель дождя, т.е. частицы, которые покидают черную дыру, движутся наружу со скоростью убегания, так что их скорость на бесконечности равна нулю. В обычных координатах GP такие частицы не могут быть описаны для r <2M. Они имеют нулевое значение для ${displaystyle {frac {dr} {dt_ {r}}}}$ в r = 2M. Это показатель того, что черная дыра Шварцшильда имеет два горизонта: горизонт прошлого и горизонт будущего. Исходная форма координат GP является регулярной на горизонте будущего (куда частицы падают, когда они падают в черную дыру), в то время как альтернативная отрицательная версия является регулярной на горизонте прошлого (из которого частицы выходят из черной дыры, если они падают). так).

В Координаты Крускала – Секереса являются регулярными для обоих горизонтов за счет того, что метрика сильно зависит от временной координаты.

Скорости света

Предположим радиальное движение. Для света, ${displaystyle d au = 0.}$ Следовательно,

{displaystyle 0 = left (dr + left (1+ {sqrt {frac {2M} {r}}} ight) dt_ {r} ight) left (dr-left (1- {sqrt {frac {2M} {r}) }} ight), dt_ {r} ight),}

{displaystyle {frac {dr} {dt_ {r}}} = pm 1- {sqrt {frac {2M} {r}}}.}

В местах очень далеко от черной дыры, ${displaystyle r o infty, {frac {dr} {dt_ {r}}} = pm 1.}$ В скорость света равно 1, как и в специальной теории относительности.
На горизонте событий ${displaystyle r = 2M,}$ скорость света, сияющего наружу от центра черной дыры, равна ${displaystyle {frac {dr} {dt_ {r}}} = 0.}$ Ему не уйти за горизонт событий. Вместо этого он застревает на горизонте событий. Поскольку свет движется быстрее, чем все остальные, материя может двигаться внутрь только на горизонте событий. Все внутри горизонта событий скрыто от внешнего мира.
Внутри горизонта событий ${displaystyle r <2M,}$ наблюдатель дождя измеряет, что свет движется к центру со скоростью более 2. Это правдоподобно. Даже в специальной теории относительности правильная скорость движущегося объекта равна
${displaystyle {frac {dr_ {ff}} {d au}} = {frac {v} {sqrt {1-v ^ {2}}}} geq 1.}$

Следует учитывать два важных момента:

Ни один объект не должен иметь скорость, превышающую скорость света, измеренную в той же системе отсчета. Таким образом, принцип причинности сохраняется. В самом деле, скорость дождя меньше скорости света: ${displaystyle {frac {left ({dfrac {dr} {dt_ {r}}} ight) _ {ext {raindrop}}} {left ({dfrac {dr} {dt_ {r}}} ight) _ {ext { light}}}} = {frac {sqrt {dfrac {2M} {r}}} {1+ {sqrt {dfrac {2M} {r}}}}} <1.}$
Время прохождения света, падающего внутрь от горизонта событий до центра черной дыры, можно получить, интегрировав уравнение для скорости света:

{displaystyle int _ {0} ^ {T_ {r}}, dt = -int _ {2M} ^ {0} left ({sqrt {frac {2M} {r}}} + 1ight) ^ {- 1}, доктор}

Результат ${displaystyle T_ {r} = 4Mln 2–2Mapprox 0,77M}$

Время в пути на свет звездная черная дыра при типичном размере в 3 массы Солнца составляет около 11 микросекунд.
Игнорирование эффектов вращения, для Стрелец А *, то огромная черная дыра проживает в центре Млечный Путь с массой 3,7 миллиона солнечных масс время прохождения света составляет около 14 секунд.
Сверхмассивная черная дыра в центре Мессье 87, гигантская эллиптическая галактика в Скопление Девы, это самая большая из известных черных дыр. Он имеет массу около 3 миллиардов солнечных масс. Свету потребуется около 3 часов, чтобы добраться до центральной сингулярности такой сверхмассивной черной дыры, а для капли дождя - 5 часов.

Взгляд наблюдателя за дождем на вселенную

Как выглядит Вселенная с точки зрения наблюдателя за дождем, погружающегося в черную дыру? ^[4] Вид можно описать следующими уравнениями:

{displaystyle cos {oldsymbol {Phi}} _ {r} = {frac {dr_ {r}} {dt_ {r}}} = {frac {{sqrt {dfrac {2M} {r}}} + cos {oldsymbol { Phi}} _ {s}} {1+ {sqrt {dfrac {2M} {r}}} cos {oldsymbol {Phi}} _ {s}}} ,,}

{displaystyle cos {oldsymbol {Phi}} _ {s} = {frac {dr_ {s}} {dt_ {s}}} = pm {sqrt {1-left (1- {frac {2M} {r}} ight ) {frac {{mathit {I}} ^ {2}} {r ^ {2}}}}} ,,!}

{displaystyle phi = {mathit {I}} int _ {r_ {0}} ^ {infty} {frac {dr} {r ^ {2} cos {oldsymbol {Phi}} _ {s}}} ,,!}

куда

{displaystyle {oldsymbol {Phi}} _ {r}, {oldsymbol {Phi}} _ {s} ,!}

- углы обзора наблюдателя за дождем и наблюдателя на оболочке по отношению к радиальному направлению наружу.

{displaystyle phi,!}

- угол между далекой звездой и направлением радиально наружу.

{displaystyle {mathit {I}} ,!}

- прицельный параметр. Каждый входящий луч света можно проследить до соответствующего луча на бесконечности. Параметр удара для входящего светового луча - это расстояние между соответствующим лучом на бесконечности и параллельным ему лучом, который погружается прямо в черную дыру.

Из-за сферической симметрии траектория света всегда лежит в плоскости, проходящей через центр сферы. Можно упростить метрику, приняв ${displaystyle heta = {frac {pi} {2}} ,!}$ .

Прицельный параметр ${displaystyle {mathit {I}} ,!}$ можно вычислить, зная координату r наблюдателя за дождем ${displaystyle r_ {0} ,!}$ и угол обзора ${displaystyle {oldsymbol {Phi}} _ {r0} ,!}$ . Тогда фактический угол ${displaystyle phi,!}$ далекой звезды, определяется численным интегрированием ${displaystyle dr ,!}$ из ${displaystyle r_ {0} ,!}$ до бесконечности. Диаграмма результатов пробы показана справа.

В р/M = 500, черная дыра еще очень далеко. Он образует в небе диаметральный угол ~ 1 градус. Звезды не сильно искажаются присутствием черной дыры, за исключением звезд непосредственно за ней. Из-за гравитационное линзирование, эти закрытые звезды теперь отклоняются на 5 градусов назад. Между этими звездами и черной дырой находится круглая полоса вторичных изображений звезд. Дубликаты изображений помогают идентифицировать черную дыру.
При r / M = 30 черная дыра стала намного больше, охватывая в небе диаметральный угол ~ 15 градусов. Полоса вторичных изображений также выросла до 10 градусов. Теперь в полосе можно найти слабые третичные изображения, которые создаются световыми лучами, которые уже когда-то огибали черную дыру. Первичные изображения более плотно распределены в остальной части неба. Схема распределения аналогична показанной ранее.
При r / M = 2, горизонте событий, черная дыра занимает значительную часть неба. Наблюдатель за дождем будет видеть область под углом до 42 градусов в радиальном направлении внутрь, которая является кромешной тьмой. Полоса вторичных и третичных изображений вместо того, чтобы увеличиваться, уменьшилась в размерах до 5 градусов. В эффект аберрации сейчас довольно доминирует. Скорость погружения достигла скорости света. Кардинально меняется картина распространения первичных образов. Первичные изображения смещаются к границе полосы. Край возле полосы теперь усыпан звездами. Из-за Эффект Допплера, на первичном изображении звезд, которые изначально находились позади наблюдателя за дождем, их изображения заметно смещены в красный цвет, тогда как те, что были впереди, смещены в синий цвет и выглядят очень яркими.
При r / M = 0,001 кривая зависимости угла далекой звезды от угла обзора, кажется, образует прямой угол при угле обзора 90 градусов. Почти все изображения звезд собраны в узкое кольцо под углом 90 градусов от радиально внутрь. Между кольцом и направлением радиально внутрь находится огромная черная дыра. С противоположной стороны слабо светят лишь несколько звезд.
Когда наблюдатель дождя приближается к сингулярности, ${displaystyle rightarrow 0 ,!}$ , и ${displaystyle cos {oldsymbol {Phi}} _ {r} ightarrow {sqrt {frac {r} {2M}}} ,!}$ . Большинство звезд и их изображений, вызванных множественными орбитами света вокруг черной дыры, сжаты до узкой полосы под углом обзора 90 °. Наблюдатель видит великолепное яркое кольцо из звезд, рассекающее темное небо пополам.

История

И Пенлеве, и Гулстранд использовали это решение, чтобы доказать, что теория Эйнштейна была неполной, поскольку она давала несколько решений для гравитационного поля сферического тела и, кроме того, давала другую физику (они утверждали, что длины стержней могут иногда быть больше, а иногда и короче в радиальное, а не тангенциальное направления). «Уловка» предложения Пенлеве заключалась в том, что он больше не придерживался полной квадратичной (статической) формы, а вместо этого допустил перекрестное пространственно-временное произведение, сделав метрическую форму больше не статической, а стационарной и не симметричной по направлению, а преимущественно ориентированной.

Во второй, более длинной статье (14 ноября 1921 г.),^[5] Пенлеве объясняет, как он получил свое решение, напрямую решая уравнения Эйнштейна для общей сферически-симметричной формы метрики. Результат, уравнение (4) его статьи, зависел от двух произвольных функций координаты r, давая двойную бесконечность решений. Теперь мы знаем, что они просто представляют собой различные варианты выбора времени и радиальных координат.

Пенлеве написал Эйнштейну, чтобы представить свое решение, и пригласил Эйнштейна в Париж для обсуждения. В ответном письме Эйнштейна (7 декабря):^[6]он извинился за то, что не сможет приехать в ближайшее время, и объяснил, почему ему не понравились аргументы Пенлеве, подчеркнув, что сами координаты не имеют значения. Наконец, в начале апреля Эйнштейн приехал в Париж. 5 апреля 1922 года на дебатах в "Коллеж де Франс" ^[7]^[8] вместе с Пенлеве, Беккерелем, Бриллюэном, Картаном, Де Дондером, Адамаром, Ланжевеном и Нордманном о «бесконечных потенциалах» Эйнштейн, сбитый с толку неквадратичным поперечным членом в линейном элементе, отверг решение Пенлеве.

Смотрите также

внешняя ссылка

[1] Поль Пенлеве, "Классическая техника и теория относительности", C. R. Acad. Sci. (Париж) 173, 677–680 (1921).

[2] Гуллстранд, Аллвар (1922). "Allgemeine Lösung des statischen Einkörperproblems in der Einsteinschen Gravitationstheorie". Arkiv för Matematik, Astronomi och Fysik. 16 (8): 1–15.

[3] Ж. Леметр (1933). «L'Univers en Expansion». Annales de la Société Scientifique de Bruxelles. A53: 51–85. Bibcode:1933АССБ ... 53 ... 51Л.

[4] Тони Ротман; Ричард Мацнер; Билл Унру (1985). «Великие иллюзии: дальнейшие разговоры на границе Пространства-Времени». В Тони Ротмане (ред.). Границы современной физики. Dover Publications (Нью-Йорк). С. 49–81.

[5] "Тяготение в механической части Ньютона и в технике Эйнштейна" C.R. Acad. Sci. (Париж) 173, 873-886 (1921).

[6] Диана Бухвальд; и др., ред. (2009). Сборник статей Альберта Эйнштейна. Princeton University Press. С. 368–370.

[7] Жан Эйзенштадт (1987). «Ранняя интерпретация решения Шварцшильда». В Дон Ховкард; Джон Стэчел (ред.). Эйнштейн и история общей теории относительности. Бирхаузер (Берлин). С. 222–223.

[8] Жан Эйзенштадт (1982). "Histoire et Singularités de la Solution de Schwarzschild (1915–1923)". Архив истории точных наук. 27: 157–198. Bibcode:1982AHES ... 27..157E. Дои:10.1007 / BF00348347 (неактивно 16.11.2020).CS1 maint: DOI неактивен по состоянию на ноябрь 2020 г. (связь)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]