Тяжелый фермионный материал - Википедия - Heavy fermion material
В физика твердого тела, тяжелые фермионы это особый тип интерметаллид, содержащий элементы с 4f или 5f электроны в незаполненном электронные полосы.[1] Электроны - это один из видов фермион, и когда они находятся в таких материалах, их иногда называют тяжелые электроны.[2] Материалы с тяжелыми фермионами обладают низкотемпературной удельная теплоемкость линейный член которого до 1000 раз больше, чем значение, ожидаемое от модель свободных электронов. Свойства соединений с тяжелыми фермионами часто связаны с частично заполненными f-орбиталями редкоземельный или же актинид ионы, которые ведут себя как локализованные магнитные моменты. Название «тяжелый фермион» происходит от того факта, что фермион ведет себя так, как если бы он эффективная масса больше, чем его масса покоя. В случае электронов ниже характерной температуры (обычно 10 К) электроны проводимости в этих металлических соединениях ведут себя так, как если бы их эффективная масса в 1000 раз превышала свободная частица масса. Эта большая эффективная масса также отражается в большом вкладе в удельное сопротивление от электрон-электронного рассеяния через Отношение Кадоваки – Вудса. Поведение тяжелых фермионов было обнаружено в широком спектре состояний, включая металлические, сверхпроводящий, изоляционный и магнитные состояния. Характерные примеры: CeCu6, CeAl3, CeCu2Si2, YbAl3, UBe13 и UPt3.
Исторический обзор
Поведение тяжелых фермионов было обнаружено К. Андресом, Дж. Э. Гребнером и Х. Р. Оттом в 1975 году, которые наблюдали огромные значения линейной удельной теплоемкости в CeAl.3.[3]
В то время как исследования легированных сверхпроводников привели к выводу, что существование локализованных магнитных моментов и сверхпроводимости в одном материале несовместимо, было показано обратное, когда в 1979 г. Франк Стеглич и другие. обнаруженный сверхпроводимость с тяжелыми фермионами в материале CeCu2Si2.[4]
Открытие квантовая критическая точка и неферми жидкость поведение на фазовой диаграмме соединений с тяжелыми фермионами Х. фон Лёнейзена и другие. в 1994 г. привел к новому всплеску интереса к исследованию этих соединений.[5] Еще одним экспериментальным прорывом стала демонстрация (группой Гил Лонзарич ), что квантовая критичность в тяжелых фермионах может быть причиной необычной сверхпроводимости.[6]
Материалы с тяжелыми фермионами играют важную роль в текущих научных исследованиях, выступая в качестве прототипов материалов для нетрадиционной сверхпроводимости, нефермижидкостного поведения и квантовой критичности. Фактическое взаимодействие между локализованными магнитными моментами и электронами проводимости в соединениях с тяжелыми фермионами до сих пор полностью не изучено и является предметом продолжающихся исследований.
Характеристики
Материалы с тяжелыми фермионами относятся к группе сильно коррелированные электронные системы.
Некоторые члены группы материалов с тяжелыми фермионами становятся сверхпроводящими при температуре ниже критической. Сверхпроводимость нетрадиционный.
При высоких температурах соединения с тяжелыми фермионами ведут себя как обычные металлы, и электроны можно описать как Ферми газ, в котором электроны считаются невзаимодействующими фермионами. В этом случае взаимодействие между ж электронами, которые представляют локальный магнитный момент, и электронами проводимости можно пренебречь.
В Теория ферми-жидкости из Лев Ландау дает хорошую модель для описания свойств материалов с наиболее тяжелыми фермионами при низких температурах. В этой теории электроны описываются квазичастицы, которые имеют такие же квантовые числа и заряд, но взаимодействие электронов учитывается введением эффективная масса, которая отличается от реальной массы свободного электрона.
Оптические свойства
Чтобы получить оптические свойства систем с тяжелыми фермионами, эти материалы были исследованы оптическими методами. спектроскопия измерения.[7] В этих экспериментах образец облучается электромагнитные волны с настраиваемым длина волны. Измерение отраженного или прошедшего света позволяет выявить характеристические энергии образца.
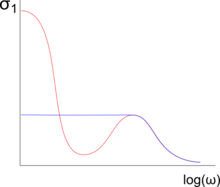
Выше характерной температуры когерентности материалы с тяжелыми фермионами ведут себя как обычные металлы; т.е. их оптический отклик описывается Модель Друде. Однако по сравнению с хорошим металлом соединения с тяжелыми фермионами при высоких температурах имеют высокую скорость рассеяния из-за большой плотности локальных магнитных моментов (по крайней мере, один f-электрон на элементарную ячейку), которые вызывают (некогерентный) Кондо рассеяние. Из-за высокой скорости рассеяния проводимость на постоянном токе и на низких частотах довольно низкая. Спад проводимости (спад Друде) происходит на частоте, соответствующей скорости релаксации.
Ниже , локализованные ж электроны гибридизуются с электронами проводимости. Это приводит к увеличению эффективной массы и возникновению гибридизационной щели. В отличие от Кондо изоляторы, химический потенциал соединений с тяжелыми фермионами находится в зоне проводимости. Эти изменения приводят к двум важным особенностям оптического отклика тяжелых фермионов.[1]
Частотно-зависимая проводимость материалов с тяжелыми фермионами может быть выражена как , содержащую эффективную массу и перенормированная скорость релаксации .[8] Из-за большой эффективной массы также увеличивается перенормированное время релаксации, что приводит к узкому спаду Друде на очень низких частотах по сравнению с обычными металлами.[8][9]Самая низкая такая скорость релаксации Друде, наблюдаемая до сих пор для тяжелых фермионов, в области низких Диапазон ГГц, был найден в UPd2Al3.[10]
Щелевая особенность оптической проводимости непосредственно представляет собой гибридизационную щель, которая открывается из-за взаимодействия локализованных f-электронов и электронов проводимости. Поскольку проводимость не исчезает полностью, наблюдаемая щель фактически является псевдощель.[11] На еще более высоких частотах наблюдается локальный максимум оптической проводимости из-за нормальных межзонных возбуждений.[1]
Теплоемкость
Удельная теплоемкость нормальных металлов
При низкой температуре и для обычных металлов удельная теплоемкость состоит из теплоемкости электронов которая линейно зависит от температуры и теплоемкости колебаний кристаллической решетки (фононы ) которая кубически зависит от температуры
с константами пропорциональности и .
В указанном выше диапазоне температур электронный вклад составляет основную часть теплоемкости. в модель свободных электронов - простая модельная система, которая не учитывает взаимодействие электронов - или металлы, которые могут быть описаны ею, электронная удельная теплоемкость дан кем-то
с Постоянная Больцмана , электронная плотность и Энергия Ферми (наивысшая одночастичная энергия занятых электронных состояний). Константа пропорциональности называется коэффициентом Зоммерфельда.
Связь теплоемкости и «тепловой эффективной массы»
Для электронов с квадратичной соотношение дисперсии (как и для газа свободных электронов) Энергия Ферми εF обратно пропорциональна массе частицы м:
куда обозначает волновое число Ферми, которое зависит от плотности электронов и является абсолютным значением волнового числа самого высокого занятого электронного состояния. Таким образом, поскольку параметр Зоммерфельда обратно пропорционально , пропорциональна массе частицы и при больших значениях , металл ведет себя как ферми-газ, в котором электроны проводимости имеют высокую тепловую эффективную массу.
Пример: UBe13 при низких температурах
Результаты экспериментов по теплоемкости тяжелого фермионного соединения UBe13 показывают пик при температуре около 0,75 К, который опускается до нуля с большим наклоном, если температура приближается к 0 К. Из-за этого пика фактор намного выше, чем модель свободных электронов в этом диапазоне температур. Напротив, выше 6 К теплоемкость этого соединения с тяжелыми фермионами приближается к значению, ожидаемому из теории свободных электронов.
Квантовая критичность
Наличие локального момента и делокализованных электронов проводимости приводит к конкуренции Кондо взаимодействие (что способствует немагнитному основному состоянию) и RKKY взаимодействие (который генерирует магнитоупорядоченные состояния, обычно антиферромагнитный для тяжелых фермионов). Путем подавления Температура Нееля антиферромагнетика с тяжелыми фермионами до нуля (например, путем приложения давления или магнитного поля или путем изменения состава материала), квантовый фазовый переход можно вызвать.[12] Для нескольких материалов с тяжелыми фермионами было показано, что такой квантовый фазовый переход может генерировать очень выраженные неферми-жидкостные свойства при конечных температурах. Такое квантово-критическое поведение также очень подробно изучается в контексте нетрадиционная сверхпроводимость.
Примерами материалов с тяжелыми фермионами с хорошо изученными квантово-критическими свойствами являются CeCu6-хAu,[13] CeIn3,[6] CePd2Si2,[6] YbRh2Si2, и CeCoIn5.[14][15]
Некоторые соединения тяжелых фермионов
Рекомендации
- ^ а б c П. Коулман (2007). «Тяжелые фермионы: электроны на грани магнетизма. Справочник по магнетизму и новым магнитным материалам». У Гельмута Кронмюллера; Стюарт Паркин (ред.). Справочник по магнетизму и новым магнитным материалам. 1. С. 95–148. arXiv:cond-mat / 0612006.
- ^ «Первые изображения тяжелых электронов в действии». Physorg.com. 2 июня 2010 г.
- ^ К. Андрес; J.E. Graebner; Х. Р. Отт (1975). «4ж-Формирование виртуального связанного состояния в CeAl3 при низких температурах ». Письма с физическими проверками. 35 (26): 1779–1782. Bibcode:1975ПхРвЛ..35.1779А. Дои:10.1103 / PhysRevLett.35.1779.
- ^ Стеглич, Ф .; Aarts, J .; Bredl, C.D .; Lieke, W .; Meschede, D .; Franz, W .; Шефер, Х. (1979-12-17). "Сверхпроводимость при сильном парамагнетизме Паули: CeCu2Si2". Письма с физическими проверками. 43 (25): 1892–1896. Bibcode:1979ПхРвЛ..43.1892С. Дои:10.1103 / PhysRevLett.43.1892. HDL:1887/81461.
- ^ Löhneysen, H. v .; Pietrus, T .; Portisch, G .; Schlager, H.G .; Schröder, A .; Sieck, M .; Траппманн, Т. (1994-05-16). «Неферми-жидкостное поведение в сплаве с тяжелыми фермионами при магнитной неустойчивости». Письма с физическими проверками. 72 (20): 3262–3265. Bibcode:1994ПхРвЛ..72.3262Л. Дои:10.1103 / PhysRevLett.72.3262. PMID 10056148.
- ^ а б c Mathur, N.D .; Grosche, F.M .; Julian, S.R .; Walker, I.R .; Freye, D.M .; Haselwimmer, R.K.W .; Лонзарич, Г. (1998). «Магнитно-опосредованная сверхпроводимость в соединениях тяжелых фермионов». Природа. 394 (6688): 39–43. Bibcode:1998Натура.394 ... 39М. Дои:10.1038/27838.
- ^ Л. Дегиорги (1999). «Электродинамический отклик соединений с тяжелыми электронами». Обзоры современной физики. 71 (3): 687–734. Bibcode:1999РвМП ... 71..687Д. Дои:10.1103 / RevModPhys.71.687.
- ^ а б А.Дж. Миллис; П.А. Ли (1987). «Разложение с большим орбитальным вырождением для решеточной модели Андерсона». Физический обзор B. 35 (7): 3394–3414. Bibcode:1987ПхРвБ..35.3394М. Дои:10.1103 / PhysRevB.35.3394.
- ^ М. Шеффлер; К. Шлегель; К. Клаусс; Д. Хафнер; C. Fella; М. Дрессель; М. Журдан; J. Sichelschmidt; К. Крелльнер; К. Гейбель; Ф. Стеглич (2013). "Микроволновая спектроскопия систем с тяжелыми фермионами: исследование динамики зарядов и магнитных моментов". Физика Статус Solidi B. 250 (3): 439–449. arXiv:1303.5011. Bibcode:2013ПССБР.250..439С. Дои:10.1002 / pssb.201200925.
- ^ М. Шеффлер; М. Дрессель; М. Журдан; Х. Адриан (2005). «Чрезвычайно медленная друде релаксация коррелированных электронов». Природа. 438 (7071): 1135–1137. Bibcode:2005 Натур.438.1135S. Дои:10.1038 / природа04232. PMID 16372004.
- ^ С. Донован; А. Шварц; Г. Грюнер (1997). «Наблюдение оптической псевдощели в UPt3". Письма с физическими проверками. 79 (7): 1401–1404. Bibcode:1997ПхРвЛ..79.1401Д. Дои:10.1103 / PhysRevLett.79.1401.
- ^ Гильберт против Лёнейзена; и другие. (2007). «Ферми-жидкостные неустойчивости при магнитных квантовых фазовых переходах». Обзоры современной физики. 79 (3): 1015–1075. arXiv:cond-mat / 0606317. Bibcode:2007РвМП ... 79.1015Л. Дои:10.1103 / RevModPhys.79.1015.
- ^ H.v. Löhneysen; и другие. (1994). «Неферми-жидкостное поведение в сплаве с тяжелыми фермионами при магнитной неустойчивости». Письма с физическими проверками. 72 (20): 3262–3265. Bibcode:1994ПхРвЛ..72.3262Л. Дои:10.1103 / PhysRevLett.72.3262. PMID 10056148.
- ^ J. Paglione; и другие. (2003). "Индуцированная полем квантовая критическая точка в CeCoIn5". Письма с физическими проверками. 91 (24): 246405. arXiv:cond-mat / 0212502. Bibcode:2003ПхРвЛ..91х6405П. Дои:10.1103 / PhysRevLett.91.246405. PMID 14683139.
- ^ А. Бьянки; и другие. (2003). «Избежание антиферромагнитного порядка и квантовой критической точки в CeCoIn5». Письма с физическими проверками. 91 (25): 257001. arXiv:cond-mat / 0302226. Bibcode:2003ПхРвЛ..91у7001Б. Дои:10.1103 / PhysRevLett.91.257001. PMID 14754138.
дальнейшее чтение
- Киттель, Чарльз (1996) Введение в физику твердого тела, 7-е изд., John Wiley and Sons, Inc.
- Мардер, М. (2000), Физика конденсированного состояния, John Wiley & Sons, Нью-Йорк.
- Хьюсон, A.C. (1993), Проблема Кондо для тяжелых фермионов, Cambridge University Press.
- Фульде П. (1995), Электронные корреляции в молекулах и твердых телах, Springer, Берлин.
- Амуся, М., Попов, К., Шагинян, В., Стефанович, В. (2015). Теория тяжелофермионных соединений - теория сильно коррелированных ферми-систем. Серия Спрингера в науках о твердом теле. 182. Springer. Дои:10.1007/978-3-319-10825-4. ISBN 978-3-319-10824-7.CS1 maint: несколько имен: список авторов (связь)

















