Хендекаграммная призма - Hendecagrammic prism

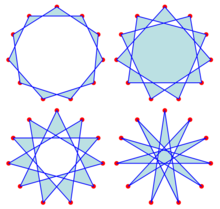
Четыре обычных хендекаграммы
{11/2}, {11/3}, {11/4} и {11/5}

В геометрия, а девушка призма это звездный многогранник сделаны из двух одинаковых обычных хендкаграммы связаны квадраты. Связанные девушка антипризмы сделаны из двух одинаковых обычных картинок, соединенных равносторонние треугольники.

Гендекаграммные призмы и бипирамиды

Есть 4 равномерные призмы и 6 антипризм.. Призмы построены по 4.4.11 / q фигуры вершин, Диаграмма Кокстера. Также даны рисунки-бипирамиды, двойники рисунков-призм.

Симметрия	Призмы
D11ч [2,11] (*2.2.11)	4.4.11/2	4.4.11/3	4.4.11/4	4.4.11/5
D11ч [2,11] (*2.2.11)

Хендекаграммные антипризмы

Антипризмы с фигурами вершин 3.3.3.3.11 / q, . Однородные антипризмы существуют при p / q> 3/2,^[1] и называются скрещенный для p / q <2. Для шестиугольной антипризмы две скрещенные антипризмы не могут быть построены как однородные (с равносторонними треугольниками): 11/8 и 11/9.

Симметрия	Антипризмы		Скрещенные - антипризмы
D11ч [2,11] (*2.2.11)	3.3.3.11/2	3.3.3.11/4	3.3.3.11/6 3.3.3.-11/5	Неоднородный 3.3.3.11/8 3.3.3.-11/3
D11d [2+,11] (2*11)	3.3.3.11/3	3.3.3.11/5	3.3.3.11/7 3.3.3.-11/4	Неоднородный 3.3.3.11/9 3.3.3.-11/2

Гендекаграммные трапецоэдры

Андекаграммная трапецоэдры двойственны декаграмматическим антипризмам.

Симметрия	Трапецоэдры
D11ч [2,11] (*2.2.11)
D11d [2+,11] (2*11)

Смотрите также

• Призматический однородный многогранник

Рекомендации

• Кокстер, Гарольд Скотт Макдональд; Longuet-Higgins, M.S .; Миллер, Дж. К. П. (1954). «Равномерные многогранники». Философские труды Лондонского королевского общества. Серия А. Математические и физические науки.. Королевское общество. 246 (916): 401–450. Дои:10.1098 / рста.1954.0003. ISSN  0080-4614. JSTOR  91532. МИСТЕР  0062446. S2CID  202575183.CS1 maint: ref = harv (связь)

внешняя ссылка

• Вайсштейн, Эрик В. «Полиграмм». MathWorld.