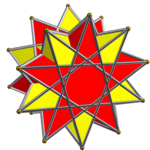
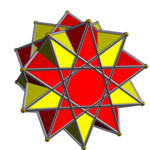
Призматический состав антипризм - Prismatic compound of antiprisms
| Соединение п п/q-гональные антипризмы | |||
|---|---|---|---|
п=2
| |||
| Тип | Равномерное соединение | ||
| Индекс |
| ||
| Многогранники | п п/q-гональный антипризмы | ||
| Символы Шлефли (n = 2) | ß {2,2p / q} ßr {2, p / q} | ||
| Диаграммы Кокстера (n = 2) | |||
| Лица | 2п {п/q} (пока не п/q=2), 2нп треугольники | ||
| Края | 4нп | ||
| Вершины | 2нп | ||
| Группа симметрии |
| ||
| Подгруппа ограничиваясь одной составляющей |
| ||
В геометрия, а призматический состав антипризмы это категория однородное соединение многогранника. Каждый член этой бесконечной семьи однородные многогранники симметричное расположение антипризмы разделяющие общую ось вращательной симметрии.
Бесконечная семья
Это бесконечное семейство можно перечислить следующим образом:
- Для каждого положительного целого числа п≥1 и для каждого рационального числа п/q> 3/2 (выражается через п и q совмещать ) встречается соединение п п/q-гональные антипризмы с группой симметрии:
- Dнпd если nq странно
- Dнпчас если nq даже
Где п/q= 2, компонент тетраэдр (или диадическая антипризма). В этом случае, если п= 2, то соединение является Stella Octangula, с более высокой симметрией (Очас).
Соединения двух антипризм
Соединения двух п-антипризмы имеют общие вершины с 2п-призма, и существуют как два чередовались множество вершин.
Декартовы координаты для вершин антипризмы с п-угольные основания и равнобедренные треугольники
с k от 0 до 2п−1; если треугольники равносторонние,
 |  |  |  |  |
| 2 двуугольный антипризмы (тетраэдры) | 2 треугольный антипризмы (октаэдры) | 2 квадрат антипризмы | 2 шестиугольник антипризмы | 2 пентаграмматический скрещенный антипризма |
Соединение двух трапецоэдров (двойников)
Двойники призматического соединения антипризм - это соединения трапецоэдры:
 Два кубика (тригональные трапецоэдры) |
Соединение трех антипризм
Для соединений трех двуугольных антипризм они повернуты на 60 градусов, а три треугольных антипризмы повернуты на 40 градусов.
 | 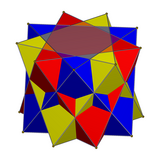 |
| Три тетраэдра | Три октаэдра |
|---|
Рекомендации
- Скиллинг, Джон (1976), "Равномерные соединения однородных многогранников", Математические труды Кембриджского философского общества, 79 (3): 447–457, Дои:10.1017 / S0305004100052440, Г-Н 0397554.
| Этот многогранник -связанная статья является заглушка. Вы можете помочь Википедии расширяя это. |