Материал Кельвина – Фойгта - Kelvin–Voigt material
А Материал Кельвина-Фойгта, также называемый Материал Voigt, это вязкоупругий материал, обладающий как свойствами эластичность и вязкость. Он назван в честь британского физика и инженера. Лорд Кельвин и после немецкого физика Вольдемар Фойгт.
Определение
Модель Кельвина-Фойгта, также называемая моделью Фойгта, может быть представлена чисто вязким демпфером и чисто упругой пружиной, соединенными параллельно, как показано на рисунке.
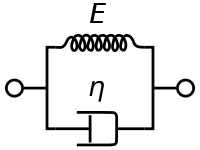
Если вместо этого мы соединим эти два элемента последовательно, мы получим модель Материал Максвелла.
Поскольку два компонента модели расположены параллельно, деформации в каждом компоненте идентичны:
где индекс D указывает напряжение-деформацию в демпфере, а индекс S указывает напряжение-деформацию в пружине. Точно так же общее напряжение будет суммой напряжений в каждом компоненте:
Из этих уравнений мы получаем, что в материале Кельвина-Фойгта стресс σ, напряжение ε и скорость их изменения во времени т регулируются уравнениями вида:
или в точечной нотации:
где E модуль упругости и это вязкость. Уравнение можно применить либо к напряжение сдвига или нормальный стресс материала.
Эффект внезапного стресса
Если мы вдруг сделаем постоянный стресс к материалу Кельвина-Фойгта, то деформации будут приближаться к деформации для чистого эластичного материала с экспоненциально убывающей разницей:
где т время и скорость релаксации . И наоборот, значение известен как время задержки.
Если бы мы освободили материал вовремя , то упругий элемент будет задерживать материал до тех пор, пока деформация не станет нулевой. Замедление подчиняется следующему уравнению:
На картинке представлена зависимость безразмерной деформации по безразмерному времени . На картинке нагрузка на материал загружается во время , и выпущенный в более позднее безразмерное время .

Поскольку вся деформация обратима (хотя и не внезапно), материал Кельвина – Фойгта является твердый.
Модель Фойгта предсказывает ползучесть более реалистично, чем модель Максвелла, потому что в бесконечном временном интервале деформация приближается к константе:
в то время как модель Максвелла предсказывает линейную зависимость между деформацией и временем, что чаще всего не так. Хотя модель Кельвина-Фойгта эффективна для прогнозирования ползучести, она не годится для описания релаксационного поведения после снятия напряженной нагрузки.
Динамический модуль
Комплекс динамический модуль материала Кельвина-Фойгта дают:
Таким образом, действительная и мнимая составляющие динамического модуля:
Обратите внимание, что постоянно, а прямо пропорциональна частоте (где кажущаяся вязкость, , - постоянная пропорциональности).
Рекомендации
- Мейерс и Чавла (1999): Раздел 13.11 Механического поведения материалов, Механическое поведение материалов, 570–580. Prentice Hall, Inc.
- http://stellar.mit.edu/S/course/3/fa06/3.032/index.html




















![E_1 = Re [E ( omega)] = E,](https://wikimedia.org/api/rest_v1/media/math/render/svg/8cf868130032cc1381ac2e232d707adcaf34d39a)
![E_2 = Im [E ( omega)] = eta omega.](https://wikimedia.org/api/rest_v1/media/math/render/svg/d0ae4630dff2c6554d25b103270f3301847eadfe)

