Список космических групп - List of space groups

Всего 230 космические группы в трех измерениях, заданных числовым индексом, и полное имя в Обозначения Германа – Могена, и короткое имя (международный короткий символ). Длинные имена даны с пробелами для удобства чтения. У каждой группы есть точечная группа элементарной ячейки.

Символы

В Обозначения Германа – Могена, пространственные группы называются символом, сочетающим точечная группа идентификатор с прописными буквами, описывающий решетчатый тип. Переводы внутри решетки в виде винтовые оси и планеры также отмечены, давая полную кристаллографическую пространственную группу.

Эти Решетки Браве в трех измерениях:

п примитивный
я по центру тела (от немецкого Innenzentriert)
F по центру лица (от немецкого "Flächenzentriert")
А с центром только на лицах A
B по центру только грани B
C с центром только на гранях C
р ромбоэдрический

Плоскость отражения м внутри точечных групп можно заменить на планер, помеченный как а, б, или c в зависимости от того, по какой оси идет скольжение. Также есть п скольжение - скольжение по половине диагонали а лицо, и d скольжение, которое проходит по четверти диагонали грани или пространства элементарной ячейки. В d скольжение часто называют алмазной плоскостью скольжения, так как это алмаз структура.

${displaystyle a}$ , ${displaystyle b}$ , или ${displaystyle c}$ скользящее перемещение по половине вектора решетки этой грани
${displaystyle n}$ скользящий перевод вместе с диагональю половины лица
${displaystyle d}$ плоскости скольжения с перемещением по четверти диагонали лица.
${displaystyle e}$ два скольжения с одной и той же плоскостью скольжения и трансляцией по двум (разным) векторам полрешетки.

Точку вращения можно заменить на ось винта обозначается числом, п, где угол поворота ${displaystyle color {Black} {frac {360 ^ {circ}} {n}}}$ . Затем степень смещения добавляется в виде индекса, показывающего, как далеко по оси находится смещение, как часть вектора параллельной решетки. Например, 2₁ представляет собой поворот на 180 ° (двукратный) с последующим переносом ½ вектора решетки. 3₁ представляет собой поворот на 120 ° (тройной) с последующим переносом вектора решетки на.

Возможные оси винта: 2₁, 3₁, 3₂, 4₁, 4₂, 4₃, 6₁, 6₂, 6₃, 6₄, и 6₅.

В Обозначение Шенфлиса, символ пространственной группы представлен символом соответствующей точечной группы с дополнительным индексом. Верхний индекс не дает никакой дополнительной информации об элементах симметрии пространственной группы, но вместо этого относится к порядку, в котором Шенфлис получил пространственные группы. Иногда это дополняется символом в виде ${displaystyle Gamma _ {x} ^ {y}}$ который задает решетку Браве. Здесь ${displaystyle xin {t, m, o, q, rh, h, c}}$ - решетчатая система, а ${displaystyle yin {emptyset, b, v, f}}$ центрирующий тип.^[1]

В Федоровский символ, тип пространственной группы обозначается как s (симморфный ), час (полусимморфный), или а (асиморфный). Число связано с порядком, в котором Федоров выводил пространственные группы. Существует 73 симморфных, 54 полусимморфных и 103 асимморфных пространственных группы.

Симморфный

73 симморфных пространственных группы могут быть получены как комбинация решеток Браве с соответствующей точечной группой. Эти группы содержат те же элементы симметрии, что и соответствующие точечные группы. Например, пространственные группы P4 / mmm ( ${displaystyle P {frac {4} {m}} {frac {2} {m}} {frac {2} {m}}}$ , 36 с) и I4 / ммм ( ${displaystyle I {frac {4} {m}} {frac {2} {m}} {frac {2} {m}}}$ , 37 с);

Полусимморфный

54 полусимморфные пространственные группы содержат только аксиальную комбинацию элементов симметрии из соответствующих точечных групп. Полусимморфные пространственные группы содержат аксиальную комбинацию 422, которая равна P4 / mcc ( ${displaystyle P {frac {4} {m}} {frac {2} {c}} {frac {2} {c}}}$ , 35ч), P4 / нмбм ( ${displaystyle P {frac {4} {n}} {frac {2} {b}} {frac {2} {m}}}$ , 36ч), P4 / nnc ( ${displaystyle P {frac {4} {n}} {frac {2} {n}} {frac {2} {c}}}$ , 37ч) и I4 / мкм ( ${displaystyle I {frac {4} {m}} {frac {2} {c}} {frac {2} {m}}}$ , 38ч).

Асимморфный

Остальные 103 пространственные группы асимморфны. Например, из точечной группы 4 / ммм ( ${displaystyle {frac {4} {m}} {frac {2} {m}} {frac {2} {m}}}$ )

Список Triclinic

Триклиническая решетка Браве

Триклинная кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Фибрифолд
1	1	${displaystyle 1}$	P1	П 1	${displaystyle Gamma _ {t} C_ {1} ^ {1}}$	1 с	${displaystyle (a / b / c) cdot 1}$	${displaystyle (circ)}$
2	1	${displaystyle imes}$	п1	п 1	${displaystyle Gamma _ {t} C_ {i} ^ {1}}$	2 с	${displaystyle (a / b / c) cdot {ilde {2}}}$	${displaystyle (2222)}$

Список моноклиники

Моноклиническая решетка Браве
просто (П)	База (С)

Моноклинная кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полные имена)		Schoenflies	Федоров	Шубников	Фибрифолд (первичный)	Фибрифолд (вторичный)
3	2	${displaystyle 22}$	P2	П 1 2 1	П 1 1 2	${displaystyle Gamma _ {m} C_ {2} ^ {1}}$	3 с	${displaystyle (b: (c / a)): 2}$	${displaystyle (2_ {0} 2_ {0} 2_ {0} 2_ {0})}$	${displaystyle ({} _ {0} {} _ {0})}$
4			P2₁	П 1 2₁ 1	П 1 1 2₁	${displaystyle Gamma _ {m} C_ {2} ^ {2}}$	1а	${displaystyle (b: (c / a)): 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} 2_ {1} 2_ {1})}$	${displaystyle ({ar {imes}} {ar {imes}})}$
5			C2	С 1 2 1	В 1 1 2	${displaystyle Gamma _ {m} ^ {b} C_ {2} ^ {3}}$	4 с	${displaystyle left ({frac {a + b} {2}} / b: (c / a) ight): 2}$	${displaystyle (2_ {0} 2_ {0} 2_ {1} 2_ {1})}$	${displaystyle ({} _ {1} {} _ {1})}$ , ${displaystyle ({*} {ar {imes}})}$
6	м	${displaystyle *}$	Вечера	P 1 м 1	P 1 1 мес.	${displaystyle Gamma _ {m} C_ {s} ^ {1}}$	5 с	${displaystyle (b: (c / a)) cdot m}$	${displaystyle [circ _ {0}]}$	${displaystyle ({} {cdot} {} {cdot})}$
7			ПК	П 1 с 1	П 1 1 б	${displaystyle Gamma _ {m} C_ {s} ^ {2}}$	1 час	${displaystyle (b: (c / a)) cdot {ilde {c}}}$	${displaystyle ({ar {circ}} _ {0})}$	${displaystyle ({} {:} {} {:})}$ , ${displaystyle ({imes} {imes} _ {0})}$
8			См	C 1 м 1	B 1 1 мес.	${displaystyle Gamma _ {m} ^ {b} C_ {s} ^ {3}}$	6 с	${displaystyle left ({frac {a + b} {2}} / b: (c / a) ight) cdot m}$	${displaystyle [circ _ {1}]}$	${displaystyle ({} {cdot} {} {:})}$ , ${displaystyle ({*} {cdot} {imes})}$
9			Копия	С 1 с 1	В 1 1 б	${displaystyle Gamma _ {m} ^ {b} C_ {s} ^ {4}}$	2ч	${displaystyle left ({frac {a + b} {2}} / b: (c / a) ight) cdot {ilde {c}}}$	${displaystyle ({ar {circ}} _ {1})}$	${displaystyle ({*} {:} {imes})}$ , ${displaystyle ({imes} {imes} _ {1})}$
10	2 / м	${displaystyle 2 *}$	P2 / м	P 1 2 / м 1	P 1 1 2 / м	${displaystyle Gamma _ {m} C_ {2h} ^ {1}}$	7 с	${displaystyle (b: (c / a)) cdot m: 2}$	${displaystyle [2_ {0} 2_ {0} 2_ {0} 2_ {0}]}$	${displaystyle [* 2 {cdot} 22 {cdot} 2)}$
11			P2₁/ м	Стр. 1 2₁/ м 1	П 1 1 2₁/ м	${displaystyle Gamma _ {m} C_ {2h} ^ {2}}$	2а	${displaystyle (b: (c / a)) cdot m: 2_ {1}}$	${displaystyle [2_ {1} 2_ {1} 2_ {1} 2_ {1}]}$	${displaystyle (22 {*} {cdot})}$
12			C2 / м	C 1 2 / м 1	B 1 1 2 / м	${displaystyle Gamma _ {m} ^ {b} C_ {2h} ^ {3}}$	8 с	${displaystyle left ({frac {a + b} {2}} / b: (c / a) ight) cdot m: 2}$	${displaystyle [2_ {0} 2_ {0} 2_ {1} 2_ {1}]}$	${displaystyle (* 2 {cdot} 22 {:} 2)}$ , ${displaystyle (2 {ar {*}} 2 {cdot} 2)}$
13			P2 / c	P 1 2 / c 1	П 1 1 2 / б	${displaystyle Gamma _ {m} C_ {2h} ^ {4}}$	3ч	${displaystyle (b: (c / a)) cdot {ilde {c}}: 2}$	${displaystyle (2_ {0} 2_ {0} 22)}$	${displaystyle (* 2 {:} 22 {:} 2)}$ , ${displaystyle (22 {*} _ {0})}$
14			P2₁/ c	Стр. 1 2₁/ с 1	П 1 1 2₁/ b	${displaystyle Gamma _ {m} C_ {2h} ^ {5}}$	3а	${displaystyle (b: (c / a)) cdot {ilde {c}}: 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} 22)}$	${displaystyle (22 {*} {:})}$ , ${displaystyle (22 {imes})}$
15			C2 / c	С 1 2 / с 1	В 1 1 2 / б	${displaystyle Gamma _ {m} ^ {b} C_ {2h} ^ {6}}$	4ч	${displaystyle left ({frac {a + b} {2}} / b: (c / a) ight) cdot {ilde {c}}: 2}$	${displaystyle (2_ {0} 2_ {1} 22)}$	${displaystyle (2 {ar {}} 2 {:} 2)}$ , ${displaystyle (22 {} _ {1})}$

Список орторомбических

Орторомбическая решетка Браве
просто (П)	Тело (Я)	Лицо (F)	База (А или С)

Орторомбическая кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Фибрифолд (первичный)	Фибрифолд (вторичный)
16	222	${displaystyle 222}$	P222	П 2 2 2	${displaystyle Gamma _ {o} D_ {2} ^ {1}}$	9 с	${displaystyle (c: a: b): 2: 2}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0})}$
17			P222₁	П 2 2 2₁	${displaystyle Gamma _ {o} D_ {2} ^ {2}}$	4а	${displaystyle (c: a: b): 2_ {1}: 2}$	${displaystyle (* 2_ {1} 2_ {1} 2_ {1} 2_ {1})}$	${displaystyle (2_ {0} 2_ {0} {*})}$
18			P2₁2₁2	П 2₁ 2₁ 2	${displaystyle Gamma _ {o} D_ {2} ^ {3}}$	7а	${displaystyle (c: a: b): 2}$ ${displaystyle 2_ {1}}$	${displaystyle (2_ {0} 2_ {0} {ar {imes}})}$	${displaystyle (2_ {1} 2_ {1} {*})}$
19			P2₁2₁2₁	П 2₁ 2₁ 2₁	${displaystyle Gamma _ {o} D_ {2} ^ {4}}$	8а	${displaystyle (c: a: b): 2_ {1}}$ ${displaystyle 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} {ar {imes}})}$
20			C222₁	С 2 2 2₁	${displaystyle Gamma _ {o} ^ {b} D_ {2} ^ {5}}$	5а	${displaystyle left ({frac {a + b} {2}}: c: a: bight): 2_ {1}: 2}$	${displaystyle (2_ {1} {*} 2_ {1} 2_ {1})}$	${displaystyle (2_ {0} 2_ {1} {*})}$
21			C222	С 2 2 2	${displaystyle Gamma _ {o} ^ {b} D_ {2} ^ {6}}$	10 с	${displaystyle left ({frac {a + b} {2}}: c: a: bight): 2: 2}$	${displaystyle (2_ {0} {*} 2_ {0} 2_ {0})}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {1} 2_ {1})}$
22			F222	Ж 2 2 2	${displaystyle Gamma _ {o} ^ {f} D_ {2} ^ {7}}$	12 с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: c: a: bight): 2: 2 }$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1})}$
23			I222	Я 2 2 2	${displaystyle Gamma _ {o} ^ {v} D_ {2} ^ {8}}$	11 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight): 2: 2}$	${displaystyle (2_ {1} {*} 2_ {0} 2_ {0})}$
24			I2₁2₁2₁	Я 2₁ 2₁ 2₁	${displaystyle Gamma _ {o} ^ {v} D_ {2} ^ {9}}$	6а	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight): 2: 2_ {1}}$	${displaystyle (2_ {0} {*} 2_ {1} 2_ {1})}$
25	мм2	${displaystyle * 22}$	Pmm2	P м м 2	${displaystyle Gamma _ {o} C_ {2v} ^ {1}}$	13 с	${displaystyle (c: a: b): mcdot 2}$	${displaystyle (* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2)}$	${displaystyle [{} _ {0} {cdot} {} _ {0} {cdot}]}$
26			Pmc2₁	P m c 2₁	${displaystyle Gamma _ {o} C_ {2v} ^ {2}}$	9а	${displaystyle (c: a: b): {ilde {c}} cdot 2_ {1}}$	${displaystyle (* {cdot} 2 {:} 2 {cdot} 2 {:} 2)}$	${displaystyle ({ar {}} {cdot} {ar {}} {cdot})}$ , ${displaystyle [{imes _ {0}} {imes _ {0}}]}$
27			Pcc2	P c c 2	${displaystyle Gamma _ {o} C_ {2v} ^ {3}}$	5ч	${displaystyle (c: a: b): {ilde {c}} cdot 2}$	${displaystyle (* {:} 2 {:} 2 {:} 2 {:} 2)}$	${displaystyle ({ar {}} _ {0} {ar {}} _ {0})}$
28			Pma2	П м а 2	${displaystyle Gamma _ {o} C_ {2v} ^ {4}}$	6ч	${displaystyle (c: a: b): {ilde {a}} cdot 2}$	${displaystyle (2_ {0} 2_ {0} {*} {cdot})}$	${displaystyle [{} _ {0} {:} {} _ {0} {:}]}$ , ${displaystyle (* {cdot} {*} _ {0})}$
29			Pca2₁	P c a 2₁	${displaystyle Gamma _ {o} C_ {2v} ^ {5}}$	11а	${displaystyle (c: a: b): {ilde {a}} cdot 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} {*} {:})}$	${displaystyle ({ar {}} {:} {ar {}} {:})}$
30			Pnc2	P n c 2	${displaystyle Gamma _ {o} C_ {2v} ^ {6}}$	7ч	${displaystyle (c: a: b): {ilde {c}} odot 2}$	${displaystyle (2_ {0} 2_ {0} {*} {:})}$	${displaystyle ({ar {}} _ {1} {ar {}} _ {1})}$ , ${displaystyle ({*} _ {0} {imes} _ {0})}$
31			Pmn2₁	П м п 2₁	${displaystyle Gamma _ {o} C_ {2v} ^ {7}}$	10а	${displaystyle (c: a: b): {widetilde {ac}} cdot 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} {*} {cdot})}$	${displaystyle (* {cdot} {ar {imes}})}$ , ${displaystyle [{imes} _ {0} {imes} _ {1}]}$
32			Pba2	П б а 2	${displaystyle Gamma _ {o} C_ {2v} ^ {8}}$	9ч	${displaystyle (c: a: b): {ilde {a}} odot 2}$	${displaystyle (2_ {0} 2_ {0} {imes} _ {0})}$	${displaystyle (* {:} {*} _ {0})}$
33			Pna2₁	П п а 2₁	${displaystyle Gamma _ {o} C_ {2v} ^ {9}}$	12а	${displaystyle (c: a: b): {ilde {a}} odot 2_ {1}}$	${displaystyle (2_ {1} 2_ {1} {imes})}$	${displaystyle (* {:} {imes})}$ , ${displaystyle ({imes} {imes} _ {1})}$
34			Pnn2	P n n 2	${displaystyle Gamma _ {o} C_ {2v} ^ {10}}$	8ч	${displaystyle (c: a: b): {widetilde {ac}} odot 2}$	${displaystyle (2_ {0} 2_ {0} {imes} _ {1})}$	${displaystyle (* _ {0} {imes} _ {1})}$
35			Cmm2	См м 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {11}}$	14 с	${displaystyle left ({frac {a + b} {2}}: c: a: bight): mcdot 2}$	${displaystyle (2_ {0} {*} {cdot} 2 {cdot} 2)}$	${displaystyle [* _ {0} {cdot} {*} _ {0} {:}]}$
36			Cmc2₁	C m c 2₁	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {12}}$	13а	${displaystyle left ({frac {a + b} {2}}: c: a: bight): {ilde {c}} cdot 2_ {1}}$	${displaystyle (2_ {1} {*} {cdot} 2 {:} 2)}$	${displaystyle ({ar {}} {cdot} {ar {}} {:})}$ , ${displaystyle [{imes} _ {1} {imes} _ {1}]}$
37			Ccc2	C c c 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {13}}$	10ч	${displaystyle left ({frac {a + b} {2}}: c: a: bight): {ilde {c}} cdot 2}$	${displaystyle (2_ {0} {*} {:} 2 {:} 2)}$	${displaystyle ({ar {}} _ {0} {ar {}} _ {1})}$
38			Amm2	А м м 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {14}}$	15 с	${displaystyle left ({frac {b + c} {2}} / c: a: bight): mcdot 2}$	${displaystyle (* {cdot} 2 {cdot} 2 {cdot} 2 {:} 2)}$	${displaystyle [{} _ {1} {cdot} {} _ {1} {cdot}]}$ , ${displaystyle [* {cdot} {imes} _ {0}]}$
39			Aem2	А б м 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {15}}$	11ч	${displaystyle left ({frac {b + c} {2}} / c: a: bight): mcdot 2_ {1}}$	${displaystyle (* {cdot} 2 {:} 2 {:} 2 {:} 2)}$	${displaystyle [{} _ {1} {:} {} _ {1} {:}]}$ , ${displaystyle ({ar {}} {cdot} {ar {}} _ {0})}$
40			Ама2	А м а 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {16}}$	12ч	${displaystyle left ({frac {b + c} {2}} / c: a: bight): {ilde {a}} cdot 2}$	${displaystyle (2_ {0} 2_ {1} {*} {cdot})}$	${displaystyle (* {cdot} {} _ {1})}$ , ${displaystyle [ {:} {imes} _ {1}]}$
41			Aea2	А б а 2	${displaystyle Gamma _ {o} ^ {b} C_ {2v} ^ {17}}$	13ч	${displaystyle left ({frac {b + c} {2}} / c: a: bight): {ilde {a}} cdot 2_ {1}}$	${displaystyle (2_ {0} 2_ {1} {*} {:})}$	${displaystyle (* {:} {} _ {1})}$ , ${displaystyle ({ar {}} {:} {ar {*}} _ {1})}$
42			Fmm2	F м м 2	${displaystyle Gamma _ {o} ^ {f} C_ {2v} ^ {18}}$	17 с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: c: a: bight): mcdot 2}$	${displaystyle (* {cdot} 2 {cdot} 2 {:} 2 {:} 2)}$	${displaystyle [{} _ {1} {cdot} {} _ {1} {:}]}$
43			Fdd2	F dd2	${displaystyle Gamma _ {o} ^ {f} C_ {2v} ^ {19}}$	16ч	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: c: a: bight): {frac { 1} {2}} {widetilde {ac}} odot 2}$	${displaystyle (2_ {0} 2_ {1} {imes})}$	${displaystyle ({*} _ {1} {imes})}$
44			Imm2	Я м м 2	${displaystyle Gamma _ {o} ^ {v} C_ {2v} ^ {20}}$	16 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight): mcdot 2}$	${displaystyle (2_ {1} {*} {cdot} 2 {cdot} 2)}$	${displaystyle [* {cdot} {imes} _ {1}]}$
45			Iba2	Я б а 2	${displaystyle Gamma _ {o} ^ {v} C_ {2v} ^ {21}}$	15ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight): {ilde {c}} cdot 2}$	${displaystyle (2_ {1} {*} {:} 2 {:} 2)}$	${displaystyle ({ar {}} {:} {ar {}} _ {0})}$
46			Ima2	Я 2	${displaystyle Gamma _ {o} ^ {v} C_ {2v} ^ {22}}$	14ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight): {ilde {a}} cdot 2}$	${displaystyle (2_ {0} {*} {cdot} 2 {:} 2)}$	${displaystyle ({ar {}} {cdot} {ar {}} _ {1})}$ , ${displaystyle [* {:} {imes} _ {0}]}$
47	${displaystyle {frac {2} {m}} {frac {2} {m}} {frac {2} {m}}}$	${displaystyle * 222}$	Пммм	P 2 / м 2 / м 2 / м	${displaystyle Gamma _ {o} D_ {2h} ^ {1}}$	18 с	${displaystyle left (c: a: bight) cdot m: 2cdot m}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2]}$
48			Пннн	P 2 / n 2 / n 2 / n	${displaystyle Gamma _ {o} D_ {2h} ^ {2}}$	19ч	${displaystyle left (c: a: bight) cdot {widetilde {ab}}: 2odot {widetilde {ac}}}$	${displaystyle (2 {ar {*}} _ {1} 2_ {0} 2_ {0}}$
49			Pccm	P 2 / c 2 / c 2 / м	${displaystyle Gamma _ {o} D_ {2h} ^ {3}}$	17ч	${displaystyle left (c: a: bight) cdot m: 2cdot {ilde {c}}}$	${displaystyle [* {:} 2 {:} 2 {:} 2 {:} 2]}$	${displaystyle (* 2_ {0} 2_ {0} 2 {cdot} 2)}$
50			Пбан	П 2 / б 2 / а 2 / н	${displaystyle Gamma _ {o} D_ {2h} ^ {4}}$	18ч	${displaystyle left (c: a: bight) cdot {widetilde {ab}}: 2odot {ilde {a}}}$	${displaystyle (2 {ar {*}} _ {0} 2_ {0} 2_ {0})}$	${displaystyle (* 2_ {0} 2_ {0} 2 {:} 2)}$
51			PMMA	П 2₁/ м 2 / м 2 / год	${displaystyle Gamma _ {o} D_ {2h} ^ {5}}$	14а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2cdot m}$	${displaystyle [2_ {0} 2_ {0} {*} {cdot}]}$	${displaystyle [* {cdot} 2 {:} 2 {cdot} 2 {:} 2]}$ , ${displaystyle [* 2 {cdot} 2 {cdot} 2 {cdot} 2]}$
52			Пнна	P 2 / № 2₁/ п 2 / а	${displaystyle Gamma _ {o} D_ {2h} ^ {6}}$	17а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2odot {widetilde {ac}}}$	${displaystyle (2_ {0} 2 {ar {*}} _ {1})}$	${displaystyle (2_ {0} {} 2 {:} 2)}$ , ${displaystyle (2 {ar {}} 2_ {1} 2_ {1})}$
53			PMNA	P 2 / м 2 / н 2₁/ а	${displaystyle Gamma _ {o} D_ {2h} ^ {7}}$	15а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2_ {1} cdot {widetilde {ac}}}$	${displaystyle [2_ {0} 2_ {0} {*} {:}]}$	${displaystyle (* 2_ {1} 2_ {1} 2 {cdot} 2)}$ , ${displaystyle (2_ {0} {*} 2 {cdot} 2)}$
54			Pcca	П 2₁/ c 2 / c 2 / а	${displaystyle Gamma _ {o} D_ {2h} ^ {8}}$	16а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2cdot {ilde {c}}}$	${displaystyle (2_ {0} 2 {ar {*}} _ {0})}$	${displaystyle (* 2 {:} 2 {:} 2 {:} 2)}$ , ${displaystyle (* 2_ {1} 2_ {1} 2 {:} 2)}$
55			Пбам	П 2₁/Би 2₁/ а 2 / м	${displaystyle Gamma _ {o} D_ {2h} ^ {9}}$	22а	${displaystyle left (c: a: bight) cdot m: 2odot {ilde {a}}}$	${displaystyle [2_ {0} 2_ {0} {imes} _ {0}]}$	${displaystyle (* 2 {cdot} 2 {:} 2 {cdot} 2)}$
56			Pccn	П 2₁/ с 2₁/ c 2 / n	${displaystyle Gamma _ {o} D_ {2h} ^ {10}}$	27а	${displaystyle left (c: a: bight) cdot {widetilde {ab}}: 2cdot {ilde {c}}}$	${displaystyle (2 {ar {*}} {:} 2 {:} 2)}$	${displaystyle (2_ {1} 2 {ar {*}} _ {0})}$
57			Пбсм	П 2 / б 2₁/ с 2₁/ м	${displaystyle Gamma _ {o} D_ {2h} ^ {11}}$	23а	${displaystyle left (c: a: bight) cdot m: 2_ {1} odot {ilde {c}}}$	${displaystyle (2_ {0} 2 {ar {*}} {cdot})}$	${displaystyle (* 2 {:} 2 {cdot} 2 {:} 2)}$ , ${displaystyle [2_ {1} 2_ {1} {*} {:}]}$
58			Pnnm	П 2₁/ п 2₁/ п 2 / м	${displaystyle Gamma _ {o} D_ {2h} ^ {12}}$	25а	${displaystyle left (c: a: bight) cdot m: 2odot {widetilde {ac}}}$	${displaystyle [2_ {0} 2_ {0} {imes} _ {1}]}$	${displaystyle (2_ {1} {*} 2 {cdot} 2)}$
59			Пммн	П 2₁/ м 2₁/ м 2 / н	${displaystyle Gamma _ {o} D_ {2h} ^ {13}}$	24а	${displaystyle left (c: a: bight) cdot {widetilde {ab}}: 2cdot m}$	${displaystyle (2 {ar {*}} {cdot} 2 {cdot} 2)}$	${displaystyle [2_ {1} 2_ {1} {*} {cdot}]}$
60			ПБХН	П 2₁/ б 2 / с 2₁/ п	${displaystyle Gamma _ {o} D_ {2h} ^ {14}}$	26а	${displaystyle left (c: a: bight) cdot {widetilde {ab}}: 2_ {1} odot {ilde {c}}}$	${displaystyle (2_ {0} 2 {ar {*}} {:})}$	${displaystyle (2_ {1} {} 2 {:} 2)}$ , ${displaystyle (2_ {1} 2 {ar {}} _ {1})}$
61			Pbca	П 2₁/Би 2₁/ с 2₁/ а	${displaystyle Gamma _ {o} D_ {2h} ^ {15}}$	29а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2_ {1} odot {ilde {c}}}$	${displaystyle (2_ {1} 2 {ar {*}} {:})}$
62			ПНМА	П 2₁/ п 2₁/ м 2₁/ а	${displaystyle Gamma _ {o} D_ {2h} ^ {16}}$	28а	${displaystyle left (c: a: bight) cdot {ilde {a}}: 2_ {1} odot m}$	${displaystyle (2_ {1} 2 {ar {*}} {cdot})}$	${displaystyle (2 {ar {*}} {cdot} 2 {:} 2)}$ , ${displaystyle [2_ {1} 2_ {1} {imes}]}$
63			См	С 2 / м 2 / с 2₁/ м	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {17}}$	18а	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot m: 2_ {1} cdot {ilde {c}}}$	${displaystyle [2_ {0} 2_ {1} {*} {cdot}]}$	${displaystyle (* 2 {cdot} 2 {cdot} 2 {:} 2)}$ , ${displaystyle [2_ {1} {*} {cdot} 2 {:} 2]}$
64			CMCA	С 2 / м 2 / с 2₁/ а	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {18}}$	19а	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot {ilde {a}}: 2_ {1} cdot {ilde {c}}}$	${displaystyle [2_ {0} 2_ {1} {*} {:}]}$	${displaystyle (* 2 {cdot} 2 {:} 2 {:} 2)}$ , ${displaystyle (* 2_ {1} 2 {cdot} 2 {:} 2)}$
65			Смм	C 2 / м 2 / м 2 / м	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {19}}$	19 с	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot m: 2cdot m}$	${displaystyle [2_ {0} {*} {cdot} 2 {cdot} 2]}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {:} 2]}$
66			Cccm	C 2 / c 2 / c 2 / м	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {20}}$	20ч	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot m: 2cdot {ilde {c}}}$	${displaystyle [2_ {0} {*} {:} 2 {:} 2]}$	${displaystyle (* 2_ {0} 2_ {1} 2 {cdot} 2)}$
67			Смме	С 2 / м 2 / м 2 / э	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {21}}$	21ч	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot {ilde {a}}: 2cdot m}$	${displaystyle (* 2_ {0} 2 {cdot} 2 {cdot} 2)}$	${displaystyle [* {cdot} 2 {:} 2 {:} 2 {:} 2]}$
68			Ccce	С 2 / с 2 / с 2 / е	${displaystyle Gamma _ {o} ^ {b} D_ {2h} ^ {22}}$	22ч	${displaystyle left ({frac {a + b} {2}}: c: a: bight) cdot {ilde {a}}: 2cdot {ilde {c}}}$	${displaystyle (* 2_ {0} 2 {:} 2 {:} 2)}$	${displaystyle (* 2_ {0} 2_ {1} 2 {:} 2)}$
69			Фммм	F 2 / м 2 / м 2 / м	${displaystyle Gamma _ {o} ^ {f} D_ {2h} ^ {23}}$	21 с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: c: a: bight) cdot m: 2cdot м}$	${displaystyle [* {cdot} 2 {cdot} 2 {:} 2 {:} 2]}$
70			Fddd	F 2 / d 2 / d 2 / d	${displaystyle Gamma _ {o} ^ {f} D_ {2h} ^ {24}}$	24ч	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: c: a: bight) cdot {frac { 1} {2}} {widetilde {ab}}: 2odot {frac {1} {2}} {widetilde {ac}}}$	${displaystyle (2 {ar {*}} 2_ {0} 2_ {1})}$
71			Immm	I 2 / м 2 / м 2 / м	${displaystyle Gamma _ {o} ^ {v} D_ {2h} ^ {25}}$	20 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight) cdot m: 2cdot m}$	${displaystyle [2_ {1} {*} {cdot} 2 {cdot} 2]}$
72			Ибам	I 2 / b 2 / a 2 / м	${displaystyle Gamma _ {o} ^ {v} D_ {2h} ^ {26}}$	23ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight) cdot m: 2cdot {ilde {c}}}$	${displaystyle [2_ {1} {*} {:} 2 {:} 2]}$	${displaystyle (* 2_ {0} 2 {cdot} 2 {:} 2)}$
73			Ибка	И 2 / б 2 / с 2 / а	${displaystyle Gamma _ {o} ^ {v} D_ {2h} ^ {27}}$	21а	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight) cdot {ilde {a}}: 2cdot {ilde {c}}}$	${displaystyle (* 2_ {1} 2 {:} 2 {:} 2)}$
74			Имма	I 2 / м 2 / м 2 / год	${displaystyle Gamma _ {o} ^ {v} D_ {2h} ^ {28}}$	20а	${displaystyle left ({frac {a + b + c} {2}} / c: a: bight) cdot {ilde {a}}: 2cdot m}$	${displaystyle (* 2_ {1} 2 {cdot} 2 {cdot} 2)}$	${displaystyle [2_ {0} {*} {cdot} 2 {:} 2]}$

Список тетрагональных

Тетрагональная решетка Браве
просто (П)	Тело (Я)

Тетрагональная кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Фибрифолд
75	4	${displaystyle 44}$	P4	Стр. 4	${displaystyle Gamma _ {q} C_ {4} ^ {1}}$	22 с	${displaystyle (c: a: a): 4}$	${displaystyle (4_ {0} 4_ {0} 2_ {0})}$
76			P4₁	Стр. 4₁	${displaystyle Gamma _ {q} C_ {4} ^ {2}}$	30а	${displaystyle (c: a: a): 4_ {1}}$	${displaystyle (4_ {1} 4_ {1} 2_ {1})}$
77			P4₂	Стр. 4₂	${displaystyle Gamma _ {q} C_ {4} ^ {3}}$	33а	${displaystyle (c: a: a): 4_ {2}}$	${displaystyle (4_ {2} 4_ {2} 2_ {0})}$
78			P4₃	Стр. 4₃	${displaystyle Gamma _ {q} C_ {4} ^ {4}}$	31а	${displaystyle (c: a: a): 4_ {3}}$	${displaystyle (4_ {1} 4_ {1} 2_ {1})}$
79			I4	Я 4	${displaystyle Gamma _ {q} ^ {v} C_ {4} ^ {5}}$	23 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4}$	${displaystyle (4_ {2} 4_ {0} 2_ {1})}$
80			I4₁	Я 4₁	${displaystyle Gamma _ {q} ^ {v} C_ {4} ^ {6}}$	32а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4_ {1}}$	${displaystyle (4_ {3} 4_ {1} 2_ {0})}$
81	4	${displaystyle 2 imes}$	п4	п 4	${displaystyle Gamma _ {q} S_ {4} ^ {1}}$	26сек	${displaystyle (c: a: a): {ilde {4}}}$	${displaystyle (442_ {0})}$
82	4	${displaystyle 2 imes}$	я4	я 4	${displaystyle Gamma _ {q} ^ {v} S_ {4} ^ {2}}$	27 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): {ilde {4}}}$	${displaystyle (442_ {1})}$
83	4 / м	${displaystyle 4 *}$	P4 / м	P 4 / м	${displaystyle Gamma _ {q} C_ {4h} ^ {1}}$	28 с	${displaystyle (c: a: a) cdot m: 4}$	${displaystyle [4_ {0} 4_ {0} 2_ {0}]}$
84			P4₂/ м	Стр. 4₂/ м	${displaystyle Gamma _ {q} C_ {4h} ^ {2}}$	41а	${displaystyle (c: a: a) cdot m: 4_ {2}}$	${displaystyle [4_ {2} 4_ {2} 2_ {0}]}$
85			P4 / n	P 4 / n	${displaystyle Gamma _ {q} C_ {4h} ^ {3}}$	29ч	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4}$	${displaystyle (44_ {0} 2)}$
86			P4₂/ п	Стр. 4₂/ п	${displaystyle Gamma _ {q} C_ {4h} ^ {4}}$	42а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4_ {2}}$	${displaystyle (44_ {2} 2)}$
87			I4 / м	Я 4 / м	${displaystyle Gamma _ {q} ^ {v} C_ {4h} ^ {5}}$	29 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot m: 4}$	${displaystyle [4_ {2} 4_ {0} 2_ {1}]}$
88			I4₁/ а	Я 4₁/ а	${displaystyle Gamma _ {q} ^ {v} C_ {4h} ^ {6}}$	40а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot {ilde {a}}: 4_ {1}}$	${displaystyle (44_ {1} 2)}$
89	422	${displaystyle 224}$	P422	П 4 2 2	${displaystyle Gamma _ {q} D_ {4} ^ {1}}$	30-е годы	${displaystyle (c: a: a): 4: 2}$	${displaystyle (* 4_ {0} 4_ {0} 2_ {0})}$
90			P42₁2	P42₁2	${displaystyle Gamma _ {q} D_ {4} ^ {2}}$	43а	${displaystyle (c: a: a): 4}$ ${displaystyle 2_ {1}}$	${displaystyle (4_ {0} {*} 2_ {0})}$
91			P4₁22	Стр. 4₁ 2 2	${displaystyle Gamma _ {q} D_ {4} ^ {3}}$	44а	${displaystyle (c: a: a): 4_ {1}: 2}$	${displaystyle (* 4_ {1} 4_ {1} 2_ {1})}$
92			P4₁2₁2	Стр. 4₁ 2₁ 2	${displaystyle Gamma _ {q} D_ {4} ^ {4}}$	48а	${displaystyle (c: a: a): 4_ {1}}$ ${displaystyle 2_ {1}}$	${displaystyle (4_ {1} {*} 2_ {1})}$
93			P4₂22	Стр. 4₂ 2 2	${displaystyle Gamma _ {q} D_ {4} ^ {5}}$	47а	${displaystyle (c: a: a): 4_ {2}: 2}$	${displaystyle (* 4_ {2} 4_ {2} 2_ {0})}$
94			P4₂2₁2	Стр. 4₂ 2₁ 2	${displaystyle Gamma _ {q} D_ {4} ^ {6}}$	50а	${displaystyle (c: a: a): 4_ {2}}$ ${displaystyle 2_ {1}}$	${displaystyle (4_ {2} {*} 2_ {0})}$
95			P4₃22	Стр. 4₃ 2 2	${displaystyle Gamma _ {q} D_ {4} ^ {7}}$	45а	${displaystyle (c: a: a): 4_ {3}: 2}$	${displaystyle (* 4_ {1} 4_ {1} 2_ {1})}$
96			P4₃2₁2	Стр. 4₃ 2₁ 2	${displaystyle Gamma _ {q} D_ {4} ^ {8}}$	49а	${displaystyle (c: a: a): 4_ {3}}$ ${displaystyle 2_ {1}}$	${displaystyle (4_ {1} {*} 2_ {1})}$
97			I422	Я 4 2 2	${displaystyle Gamma _ {q} ^ {v} D_ {4} ^ {9}}$	31 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4: 2}$	${displaystyle (* 4_ {2} 4_ {0} 2_ {1})}$
98			I4₁22	Я 4₁ 2 2	${displaystyle Gamma _ {q} ^ {v} D_ {4} ^ {10}}$	46а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4: 2_ {1}}$	${displaystyle (* 4_ {3} 4_ {1} 2_ {0})}$
99	4мм	${displaystyle * 44}$	P4мм	P 4 м м	${displaystyle Gamma _ {q} C_ {4v} ^ {1}}$	24 с	${displaystyle (c: a: a): 4cdot m}$	${displaystyle (* {cdot} 4 {cdot} 4 {cdot} 2)}$
100			P4bm	P 4 б м	${displaystyle Gamma _ {q} C_ {4v} ^ {2}}$	26ч	${displaystyle (c: a: a): 4odot {ilde {a}}}$	${displaystyle (4_ {0} {*} {cdot} 2)}$
101			P4₂см	Стр. 4₂ см	${displaystyle Gamma _ {q} C_ {4v} ^ {3}}$	37а	${displaystyle (c: a: a): 4_ {2} cdot {ilde {c}}}$	${displaystyle (* {:} 4 {cdot} 4 {:} 2)}$
102			P4₂нм	Стр. 4₂ п м	${displaystyle Gamma _ {q} C_ {4v} ^ {4}}$	38а	${displaystyle (c: a: a): 4_ {2} odot {widetilde {ac}}}$	${displaystyle (4_ {2} {*} {cdot} 2)}$
103			P4cc	P 4 c c	${displaystyle Gamma _ {q} C_ {4v} ^ {5}}$	25ч	${displaystyle (c: a: a): 4cdot {ilde {c}}}$	${displaystyle (* {:} 4 {:} 4 {:} 2)}$
104			P4nc	П 4 н с	${displaystyle Gamma _ {q} C_ {4v} ^ {6}}$	27ч	${displaystyle (c: a: a): 4odot {widetilde {ac}}}$	${displaystyle (4_ {0} {*} {:} 2)}$
105			P4₂MC	Стр. 4₂ м с	${displaystyle Gamma _ {q} C_ {4v} ^ {7}}$	36а	${displaystyle (c: a: a): 4_ {2} cdot m}$	${displaystyle (* {cdot} 4 {:} 4 {cdot} 2)}$
106			P4₂до н.э	Стр. 4₂ до н.э	${displaystyle Gamma _ {q} C_ {4v} ^ {8}}$	39а	${displaystyle (c: a: a): 4odot {ilde {a}}}$	${displaystyle (4_ {2} {*} {:} 2)}$
107			I4мм	Я 4 м м	${displaystyle Gamma _ {q} ^ {v} C_ {4v} ^ {9}}$	25 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4cdot m}$	${displaystyle (* {cdot} 4 {cdot} 4 {:} 2)}$
108			I4см	Я 4 см	${displaystyle Gamma _ {q} ^ {v} C_ {4v} ^ {10}}$	28ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4cdot {ilde {c}}}$	${displaystyle (* {cdot} 4 {:} 4 {:} 2)}$
109			I4₁мкр	Я 4₁ м д	${displaystyle Gamma _ {q} ^ {v} C_ {4v} ^ {11}}$	34а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4_ {1} odot m}$	${displaystyle (4_ {1} {*} {cdot} 2)}$
110			I4₁компакт диск	Я 4₁ CD	${displaystyle Gamma _ {q} ^ {v} C_ {4v} ^ {12}}$	35а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): 4_ {1} odot {ilde {c}}}$	${displaystyle (4_ {1} {*} {:} 2)}$
111	42м	${displaystyle 2 {*} 2}$	п42м	п 4 2 мес.	${displaystyle Gamma _ {q} D_ {2d} ^ {1}}$	32 с	${displaystyle (c: a: a): {ilde {4}}: 2}$	${displaystyle (* 4 {cdot} 42_ {0})}$
112			п42c	п 4 2 с	${displaystyle Gamma _ {q} D_ {2d} ^ {2}}$	30ч	${displaystyle (c: a: a): {ilde {4}}}$ ${displaystyle 2}$	${displaystyle (* 4 {:} 42_ {0})}$
113			п42₁м	п 4 2₁ м	${displaystyle Gamma _ {q} D_ {2d} ^ {3}}$	52а	${displaystyle (c: a: a): {ilde {4}} cdot {widetilde {ab}}}$	${displaystyle (4 {ar {*}} {cdot} 2)}$
114			п42₁c	п 4 2₁ c	${displaystyle Gamma _ {q} D_ {2d} ^ {4}}$	53а	${displaystyle (c: a: a): {ilde {4}} cdot {widetilde {abc}}}$	${displaystyle (4 {ar {*}} {:} 2)}$
115			п4m2	п 4 м 2	${displaystyle Gamma _ {q} D_ {2d} ^ {5}}$	33 с	${displaystyle (c: a: a): {ilde {4}} cdot m}$	${displaystyle (* {cdot} 44 {cdot} 2)}$
116			п4c2	п 4 c 2	${displaystyle Gamma _ {q} D_ {2d} ^ {6}}$	31ч	${displaystyle (c: a: a): {ilde {4}} cdot {ilde {c}}}$	${displaystyle (* {:} 44 {:} 2)}$
117			п4Би 2	п 4 Би 2	${displaystyle Gamma _ {q} D_ {2d} ^ {7}}$	32ч	${displaystyle (c: a: a): {ilde {4}} odot {ilde {a}}}$	${displaystyle (4 {ar {*}} _ {0} 2_ {0})}$
118			п4n2	п 4 п 2	${displaystyle Gamma _ {q} D_ {2d} ^ {8}}$	33ч	${displaystyle (c: a: a): {ilde {4}} cdot {widetilde {ac}}}$	${displaystyle (4 {ar {*}} _ {1} 2_ {0})}$
119			я4m2	я 4 м 2	${displaystyle Gamma _ {q} ^ {v} D_ {2d} ^ {9}}$	35 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): {ilde {4}} cdot m}$	${displaystyle (* 4 {cdot} 42_ {1})}$
120			я4c2	я 4 c 2	${displaystyle Gamma _ {q} ^ {v} D_ {2d} ^ {10}}$	34ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): {ilde {4}} cdot {ilde {c}}}$	${displaystyle (* 4 {:} 42_ {1})}$
121			я42м	я 4 2 мес.	${displaystyle Gamma _ {q} ^ {v} D_ {2d} ^ {11}}$	34с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): {ilde {4}}: 2}$	${displaystyle (* {cdot} 44 {:} 2)}$
122			я42d	я 4 2 дн.	${displaystyle Gamma _ {q} ^ {v} D_ {2d} ^ {12}}$	51а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight): {ilde {4}} odot {frac {1} {2}} {widetilde {abc}}}$	${displaystyle (4 {ar {*}} 2_ {1})}$
123	4 / м 2 / м 2 / м	${displaystyle * 224}$	P4 / ммм	P 4 / м 2 / м 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {1}}$	36 с	${displaystyle (c: a: a) cdot m: 4cdot m}$	${displaystyle [* {cdot} 4 {cdot} 4 {cdot} 2]}$
124			P4 / mcc	P 4 / м 2 / с 2 / с	${displaystyle Gamma _ {q} D_ {4h} ^ {2}}$	35ч	${displaystyle (c: a: a) cdot m: 4cdot {ilde {c}}}$	${displaystyle [* {:} 4 {:} 4 {:} 2]}$
125			P4 / нм	P 4 / n 2 / b 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {3}}$	36ч	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4odot {ilde {a}}}$	${displaystyle (* 4_ {0} 4 {cdot} 2)}$
126			P4 / nnc	P 4 / n 2 / n 2 / c	${displaystyle Gamma _ {q} D_ {4h} ^ {4}}$	37ч	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4odot {widetilde {ac}}}$	${displaystyle (* 4_ {0} 4 {:} 2)}$
127			P4 / мбм	P 4 / м 2₁/ б 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {5}}$	54а	${displaystyle (c: a: a) cdot m: 4odot {ilde {a}}}$	${displaystyle [4_ {0} {*} {cdot} 2]}$
128			P4 / mnc	P 4 / м 2₁/ п 2 / с	${displaystyle Gamma _ {q} D_ {4h} ^ {6}}$	56а	${displaystyle (c: a: a) cdot m: 4odot {widetilde {ac}}}$	${displaystyle [4_ {0} {*} {:} 2]}$
129			P4 / нм	P 4 / № 2₁/ м 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {7}}$	55а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4cdot m}$	${displaystyle (* 4 {cdot} 4 {cdot} 2)}$
130			P4 / ncc	P 4 / № 2₁/ c 2 / c	${displaystyle Gamma _ {q} D_ {4h} ^ {8}}$	57а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4cdot {ilde {c}}}$	${displaystyle (* 4 {:} 4 {:} 2)}$
131			P4₂/ mmc	Стр. 4₂/ м 2 / м 2 / с	${displaystyle Gamma _ {q} D_ {4h} ^ {9}}$	60а	${displaystyle (c: a: a) cdot m: 4_ {2} cdot m}$	${displaystyle [* {cdot} 4 {:} 4 {cdot} 2]}$
132			P4₂/ мкм	Стр. 4₂/ м 2 / с 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {10}}$	61a	${displaystyle (c: a: a) cdot m: 4_ {2} cdot {ilde {c}}}$	${displaystyle [* {:} 4 {cdot} 4 {:} 2]}$
133			P4₂/ nbc	Стр. 4₂/ п 2 / б 2 / с	${displaystyle Gamma _ {q} D_ {4h} ^ {11}}$	63а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4_ {2} odot {ilde {a}}}$	${displaystyle (* 4_ {2} 4 {:} 2)}$
134			P4₂/ нм	Стр. 4₂/ п 2 / п 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {12}}$	62а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4_ {2} odot {widetilde {ac}}}$	${displaystyle (* 4_ {2} 4 {cdot} 2)}$
135			P4₂/ mbc	Стр. 4₂/ м 2₁/ b 2 / c	${displaystyle Gamma _ {q} D_ {4h} ^ {13}}$	66a	${displaystyle (c: a: a) cdot m: 4_ {2} odot {ilde {a}}}$	${displaystyle [4_ {2} {*} {:} 2]}$
136			P4₂/ млн.	Стр. 4₂/ м 2₁/ п 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {14}}$	65а	${displaystyle (c: a: a) cdot m: 4_ {2} odot {widetilde {ac}}}$	${displaystyle [4_ {2} {*} {cdot} 2]}$
137			P4₂/ nmc	Стр. 4₂/ п 2₁/ м 2 / с	${displaystyle Gamma _ {q} D_ {4h} ^ {15}}$	67a	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4_ {2} cdot m}$	${displaystyle (* 4 {cdot} 4 {:} 2)}$
138			P4₂/ нсм	Стр. 4₂/ п 2₁/ c 2 / м	${displaystyle Gamma _ {q} D_ {4h} ^ {16}}$	65а	${displaystyle (c: a: a) cdot {widetilde {ab}}: 4_ {2} cdot {ilde {c}}}$	${displaystyle (* 4 {:} 4 {cdot} 2)}$
139			I4 / ммм	I 4 / м 2 / м 2 / м	${displaystyle Gamma _ {q} ^ {v} D_ {4h} ^ {17}}$	37 с	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot m: 4cdot m}$	${displaystyle [* {cdot} 4 {cdot} 4 {:} 2]}$
140			I4 / мкм	I 4 / м 2 / c 2 / м	${displaystyle Gamma _ {q} ^ {v} D_ {4h} ^ {18}}$	38ч	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot m: 4cdot {ilde {c}}}$	${displaystyle [* {cdot} 4 {:} 4 {:} 2]}$
141			I4₁/ драм	Я 4₁/ а 2 / м 2 / сут	${displaystyle Gamma _ {q} ^ {v} D_ {4h} ^ {19}}$	59a	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot {ilde {a}}: 4_ {1} odot m}$	${displaystyle (* 4_ {1} 4 {cdot} 2)}$
142			I4₁/ acd	Я 4₁/ а 2 / с 2 / д	${displaystyle Gamma _ {q} ^ {v} D_ {4h} ^ {20}}$	58а	${displaystyle left ({frac {a + b + c} {2}} / c: a: aight) cdot {ilde {a}}: 4_ {1} odot {ilde {c}}}$	${displaystyle (* 4_ {1} 4 {:} 2)}$

Список тригональных

Тригональная решетка Браве
Ромбоэдрический (Р)	Шестиугольный (П)

Тригональная кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Фибрифолд
143	3	${displaystyle 33}$	P3	P 3	${displaystyle Gamma _ {h} C_ {3} ^ {1}}$	38 с	${displaystyle (c: (a / a)): 3}$	${displaystyle (3_ {0} 3_ {0} 3_ {0})}$
144			P3₁	P 3₁	${displaystyle Gamma _ {h} C_ {3} ^ {2}}$	68а	${displaystyle (c: (a / a)): 3_ {1}}$	${displaystyle (3_ {1} 3_ {1} 3_ {1})}$
145			P3₂	P 3₂	${displaystyle Gamma _ {h} C_ {3} ^ {3}}$	69а	${displaystyle (c: (a / a)): 3_ {2}}$	${displaystyle (3_ {1} 3_ {1} 3_ {1})}$
146			R3	R 3	${displaystyle Gamma _ {rh} C_ {3} ^ {4}}$	39 с	${displaystyle (а / а / а) / 3}$	${displaystyle (3_ {0} 3_ {1} 3_ {2})}$
147	3	${displaystyle 3 imes}$	п3	п 3	${displaystyle Gamma _ {h} C_ {3i} ^ {1}}$	51 с	${displaystyle (c: (a / a)): {ilde {6}}}$	${displaystyle (63_ {0} 2)}$
148	3	${displaystyle 3 imes}$	р3	р 3	${displaystyle Gamma _ {rh} C_ {3i} ^ {2}}$	52 с	${displaystyle (a / a / a) / {ilde {6}}}$	${displaystyle (63_ {1} 2)}$
149	32	${displaystyle 223}$	P312	П 3 1 2	${displaystyle Gamma _ {h} D_ {3} ^ {1}}$	45 с	${displaystyle (c: (a / a)): 2: 3}$	${displaystyle (* 3_ {0} 3_ {0} 3_ {0})}$
150			P321	П 3 2 1	${displaystyle Gamma _ {h} D_ {3} ^ {2}}$	44 с	${displaystyle (c: (a / a)) cdot 2: 3}$	${displaystyle (3_ {0} {*} 3_ {0})}$
151			P3₁12	P 3₁ 1 2	${displaystyle Gamma _ {h} D_ {3} ^ {3}}$	72а	${displaystyle (c: (a / a)): 2: 3_ {1}}$	${displaystyle (* 3_ {1} 3_ {1} 3_ {1})}$
152			P3₁21	P 3₁ 2 1	${displaystyle Gamma _ {h} D_ {3} ^ {4}}$	70а	${displaystyle (c: (a / a)) cdot 2: 3_ {1}}$	${displaystyle (3_ {1} {*} 3_ {1})}$
153			P3₂12	P 3₂ 1 2	${displaystyle Gamma _ {h} D_ {3} ^ {5}}$	73а	${displaystyle (c: (a / a)): 2: 3_ {2}}$	${displaystyle (* 3_ {1} 3_ {1} 3_ {1})}$
154			P3₂21	P 3₂ 2 1	${displaystyle Gamma _ {h} D_ {3} ^ {6}}$	71a	${displaystyle (c: (a / a)) cdot 2: 3_ {2}}$	${displaystyle (3_ {1} {*} 3_ {1})}$
155			R32	R 3 2	${displaystyle Gamma _ {rh} D_ {3} ^ {7}}$	46 с	${displaystyle (а / а / а) / 3: 2}$	${displaystyle (* 3_ {0} 3_ {1} 3_ {2})}$
156	3м	${displaystyle * 33}$	P3m1	P 3 м 1	${displaystyle Gamma _ {h} C_ {3v} ^ {1}}$	40-е годы	${displaystyle (c: (a / a)): mcdot 3}$	${displaystyle (* {cdot} 3 {cdot} 3 {cdot} 3)}$
157			P31m	P 3 1 мес.	${displaystyle Gamma _ {h} C_ {3v} ^ {2}}$	41с	${displaystyle (c: (a / a)) cdot mcdot 3}$	${displaystyle (3_ {0} {*} {cdot} 3)}$
158			P3c1	П 3 с 1	${displaystyle Gamma _ {h} C_ {3v} ^ {3}}$	39ч	${displaystyle (c: (a / a)): {ilde {c}}: 3}$	${displaystyle (* {:} 3 {:} 3 {:} 3)}$
159			P31c	П 3 1 в	${displaystyle Gamma _ {h} C_ {3v} ^ {4}}$	40ч	${displaystyle (c: (a / a)) cdot {ilde {c}}: 3}$	${displaystyle (3_ {0} {*} {:} 3)}$
160			R3m	R 3 м	${displaystyle Gamma _ {rh} C_ {3v} ^ {5}}$	42с	${displaystyle (a / a / a) / 3cdot m}$	${displaystyle (3_ {1} {*} {cdot} 3)}$
161			R3c	R 3 c	${displaystyle Gamma _ {rh} C_ {3v} ^ {6}}$	41ч	${displaystyle (a / a / a) / 3cdot {ilde {c}}}$	${displaystyle (3_ {1} {*} {:} 3)}$
162	3 2 / м	${displaystyle 2 {*} 3}$	п31 мес.	п 3 1 2 / м	${displaystyle Gamma _ {h} D_ {3d} ^ {1}}$	56 с	${displaystyle (c: (a / a)) cdot mcdot {ilde {6}}}$	${displaystyle (* {cdot} 63_ {0} 2)}$
163			п31c	п 3 1 2 / с	${displaystyle Gamma _ {h} D_ {3d} ^ {2}}$	46ч	${displaystyle (c: (a / a)) cdot {ilde {c}} cdot {ilde {6}}}$	${displaystyle (* {:} 63_ {0} 2)}$
164			п3m1	п 3 2 / м 1	${displaystyle Gamma _ {h} D_ {3d} ^ {3}}$	55-е годы	${displaystyle (c: (a / a)): mcdot {ilde {6}}}$	${displaystyle (* 6 {cdot} 3 {cdot} 2)}$
165			п3c1	п 3 2 / с 1	${displaystyle Gamma _ {h} D_ {3d} ^ {4}}$	45ч	${displaystyle (c: (a / a)): {ilde {c}} cdot {ilde {6}}}$	${displaystyle (* 6 {:} 3 {:} 2)}$
166			р3м	р 3 2 / м	${displaystyle Gamma _ {rh} D_ {3d} ^ {5}}$	57 с	${displaystyle (a / a / a) / {ilde {6}} cdot m}$	${displaystyle (* {cdot} 63_ {1} 2)}$
167			р3c	р 3 2 / с	${displaystyle Gamma _ {rh} D_ {3d} ^ {6}}$	47ч	${displaystyle (a / a / a) / {ilde {6}} cdot {ilde {c}}}$	${displaystyle (* {:} 63_ {1} 2)}$

Список гексагональных

Шестиугольная решетка Браве

Гексагональная кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Фибрифолд
168	6	${displaystyle 66}$	P6	Стр. 6	${displaystyle Gamma _ {h} C_ {6} ^ {1}}$	49 с	${displaystyle (c: (a / a)): 6}$	${displaystyle (6_ {0} 3_ {0} 2_ {0})}$
169			P6₁	Стр. 6₁	${displaystyle Gamma _ {h} C_ {6} ^ {2}}$	74а	${displaystyle (c: (a / a)): 6_ {1}}$	${displaystyle (6_ {1} 3_ {1} 2_ {1})}$
170			P6₅	Стр. 6₅	${displaystyle Gamma _ {h} C_ {6} ^ {3}}$	75а	${displaystyle (c: (a / a)): 6_ {5}}$	${displaystyle (6_ {1} 3_ {1} 2_ {1})}$
171			P6₂	Стр. 6₂	${displaystyle Gamma _ {h} C_ {6} ^ {4}}$	76a	${displaystyle (c: (a / a)): 6_ {2}}$	${displaystyle (6_ {2} 3_ {2} 2_ {0})}$
172			P6₄	Стр. 6₄	${displaystyle Gamma _ {h} C_ {6} ^ {5}}$	77a	${displaystyle (c: (a / a)): 6_ {4}}$	${displaystyle (6_ {2} 3_ {2} 2_ {0})}$
173			P6₃	Стр. 6₃	${displaystyle Gamma _ {h} C_ {6} ^ {6}}$	78a	${displaystyle (c: (a / a)): 6_ {3}}$	${displaystyle (6_ {3} 3_ {0} 2_ {1})}$
174	6	${displaystyle 3 *}$	п6	п 6	${displaystyle Gamma _ {h} C_ {3h} ^ {1}}$	43с	${displaystyle (c: (a / a)): 3: m}$	${displaystyle [3_ {0} 3_ {0} 3_ {0}]}$
175	6 / м	${displaystyle 6 *}$	P6 / м	P 6 / м	${displaystyle Gamma _ {h} C_ {6h} ^ {1}}$	53 с	${displaystyle (c: (a / a)) cdot m: 6}$	${displaystyle [6_ {0} 3_ {0} 2_ {0}]}$
176	6 / м	${displaystyle 6 *}$	P6₃/ м	Стр. 6₃/ м	${displaystyle Gamma _ {h} C_ {6h} ^ {2}}$	81a	${displaystyle (c: (a / a)) cdot m: 6_ {3}}$	${displaystyle [6_ {3} 3_ {0} 2_ {1}]}$
177	622	${displaystyle 226}$	P622	П 6 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {1}}$	54с	${displaystyle (c: (a / a)) cdot 2: 6}$	${displaystyle (* 6_ {0} 3_ {0} 2_ {0})}$
178			P6₁22	Стр. 6₁ 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {2}}$	82a	${displaystyle (c: (a / a)) cdot 2: 6_ {1}}$	${displaystyle (* 6_ {1} 3_ {1} 2_ {1})}$
179			P6₅22	Стр. 6₅ 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {3}}$	83a	${displaystyle (c: (a / a)) cdot 2: 6_ {5}}$	${displaystyle (* 6_ {1} 3_ {1} 2_ {1})}$
180			P6₂22	Стр. 6₂ 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {4}}$	84а	${displaystyle (c: (a / a)) cdot 2: 6_ {2}}$	${displaystyle (* 6_ {2} 3_ {2} 2_ {0})}$
181			P6₄22	Стр. 6₄ 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {5}}$	85а	${displaystyle (c: (a / a)) cdot 2: 6_ {4}}$	${displaystyle (* 6_ {2} 3_ {2} 2_ {0})}$
182			P6₃22	Стр. 6₃ 2 2	${displaystyle Gamma _ {h} D_ {6} ^ {6}}$	86а	${displaystyle (c: (a / a)) cdot 2: 6_ {3}}$	${displaystyle (* 6_ {3} 3_ {0} 2_ {1})}$
183	6мм	${displaystyle * 66}$	P6мм	P 6 м м	${displaystyle Gamma _ {h} C_ {6v} ^ {1}}$	50-е годы	${displaystyle (c: (a / a)): mcdot 6}$	${displaystyle (* {cdot} 6 {cdot} 3 {cdot} 2)}$
184			P6cc	P 6 c c	${displaystyle Gamma _ {h} C_ {6v} ^ {2}}$	44ч	${displaystyle (c: (a / a)): {ilde {c}} cdot 6}$	${displaystyle (* {:} 6 {:} 3 {:} 2)}$
185			P6₃см	Стр. 6₃ см	${displaystyle Gamma _ {h} C_ {6v} ^ {3}}$	80a	${displaystyle (c: (a / a)): {ilde {c}} cdot 6_ {3}}$	${displaystyle (* {cdot} 6 {:} 3 {:} 2)}$
186			P6₃MC	Стр. 6₃ м с	${displaystyle Gamma _ {h} C_ {6v} ^ {4}}$	79а	${displaystyle (c: (a / a)): mcdot 6_ {3}}$	${displaystyle (* {:} 6 {cdot} 3 {cdot} 2)}$
187	6m2	${displaystyle * 223}$	п6m2	п 6 м 2	${displaystyle Gamma _ {h} D_ {3h} ^ {1}}$	48 с	${displaystyle (c: (a / a)): mcdot 3: m}$	${displaystyle [* {cdot} 3 {cdot} 3 {cdot} 3]}$
188			п6c2	п 6 c 2	${displaystyle Gamma _ {h} D_ {3h} ^ {2}}$	43ч	${displaystyle (c: (a / a)): {ilde {c}} cdot 3: m}$	${displaystyle [* {:} 3 {:} 3 {:} 3]}$
189			п62м	п 6 2 мес.	${displaystyle Gamma _ {h} D_ {3h} ^ {3}}$	47с	${displaystyle (c: (a / a)) cdot m: 3cdot m}$	${displaystyle [3_ {0} {*} {cdot} 3]}$
190			п62c	п 6 2 с	${displaystyle Gamma _ {h} D_ {3h} ^ {4}}$	42ч	${displaystyle (c: (a / a)) cdot m: 3cdot {ilde {c}}}$	${displaystyle [3_ {0} {*} {:} 3]}$
191	6 / м 2 / м 2 / м	${displaystyle * 226}$	P6 / ммм	P 6 / м 2 / м 2 / м	${displaystyle Gamma _ {h} D_ {6h} ^ {1}}$	58 с	${displaystyle (c: (a / a)) cdot m: 6cdot m}$	${displaystyle [* {cdot} 6 {cdot} 3 {cdot} 2]}$
192			P6 / mcc	P 6 / м 2 / с 2 / с	${displaystyle Gamma _ {h} D_ {6h} ^ {2}}$	48ч	${displaystyle (c: (a / a)) cdot m: 6cdot {ilde {c}}}$	${displaystyle [* {:} 6 {:} 3 {:} 2]}$
193			P6₃/ мкм	Стр. 6₃/ м 2 / с 2 / м	${displaystyle Gamma _ {h} D_ {6h} ^ {3}}$	87a	${displaystyle (c: (a / a)) cdot m: 6_ {3} cdot {ilde {c}}}$	${displaystyle [* {cdot} 6 {:} 3 {:} 2]}$
194			P6₃/ mmc	Стр. 6₃/ м 2 / м 2 / с	${displaystyle Gamma _ {h} D_ {6h} ^ {4}}$	88a	${displaystyle (c: (a / a)) cdot m: 6_ {3} cdot m}$	${displaystyle [* {:} 6 {cdot} 3 {cdot} 2]}$

Список кубических

Кубическая решетка Браве
просто (П)	По центру тела (Я)	По центру лица (F)

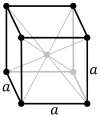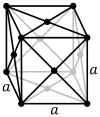Примеры кубических структур

(221) Хлорид цезия. Разные цвета для двух типов атомов.
(216) Сфалерит
(223) Структура Вира – Фелана

Кубическая кристаллическая система
Число	Группа точек	Орбифолд	Короткое имя	Полное имя	Schoenflies	Федоров	Шубников	Конвей	Фибрифолд (сохраняющий ${displaystyle z}$ )	Фибрифолд (сохраняющий ${displaystyle x}$ , ${displaystyle y}$ , ${displaystyle z}$ )
195	23	${displaystyle 332}$	P23	П 2 3	${displaystyle Gamma _ {c} T ^ {1}}$	59 с	${displaystyle left (a: a: aight): 2/3}$	${displaystyle 2 ^ {circ}}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 3}$
196			F23	Ж 2 3	${displaystyle Gamma _ {c} ^ {f} T ^ {2}}$	61с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 2/3 }$	${displaystyle 1 ^ {circ}}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 3}$
197			I23	Я 2 3	${displaystyle Gamma _ {c} ^ {v} T ^ {3}}$	60-е годы	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): 2/3}$	${displaystyle 4 ^ {circ circ}}$	${displaystyle (2_ {1} {*} 2_ {0} 2_ {0}) {:} 3}$	${displaystyle (2_ {1} {*} 2_ {0} 2_ {0}) {:} 3}$
198			P2₁3	П 2₁ 3	${displaystyle Gamma _ {c} T ^ {4}}$	89a	${displaystyle left (a: a: aight): 2_ {1} / 3}$	${displaystyle 1 ^ {circ} / 4}$	${displaystyle (2_ {1} 2_ {1} {ar {imes}}) {:} 3}$	${displaystyle (2_ {1} 2_ {1} {ar {imes}}) {:} 3}$
199			I2₁3	Я 2₁ 3	${displaystyle Gamma _ {c} ^ {v} T ^ {5}}$	90а	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): 2_ {1} / 3}$	${displaystyle 2 ^ {circ} / 4}$	${displaystyle (2_ {0} {*} 2_ {1} 2_ {1}) {:} 3}$	${displaystyle (2_ {0} {*} 2_ {1} 2_ {1}) {:} 3}$
200	2 / м 3	${displaystyle 3 {*} 2}$	Вечера3	P 2 / м 3	${displaystyle Gamma _ {c} T_ {h} ^ {1}}$	62с	${displaystyle left (a: a: aight) cdot m / {ilde {6}}}$	${displaystyle 4 ^ {-}}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2] {:} 3}$
201			Pn3	P 2 / n 3	${displaystyle Gamma _ {c} T_ {h} ^ {2}}$	49ч	${displaystyle left (a: a: aight) cdot {widetilde {ab}} / {ilde {6}}}$	${displaystyle 4 ^ {circ +}}$	${displaystyle (2 {ar {*}} _ {1} 2_ {0} 2_ {0}) {:} 3}$	${displaystyle (2 {ar {*}} _ {1} 2_ {0} 2_ {0}) {:} 3}$
202			FM3	F 2 / м 3	${displaystyle Gamma _ {c} ^ {f} T_ {h} ^ {3}}$	64 с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight) cdot m / { Ильде {6}}}$	${displaystyle 2 ^ {-}}$	${displaystyle [* {cdot} 2 {cdot} 2 {:} 2 {:} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {:} 2 {:} 2] {:} 3}$
203			Fd3	F 2 / d 3	${displaystyle Gamma _ {c} ^ {f} T_ {h} ^ {4}}$	50ч	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight) cdot {frac { 1} {2}} {widetilde {ab}} / {ilde {6}}}$	${displaystyle 2 ^ {circ +}}$	${displaystyle (2 {ar {*}} 2_ {0} 2_ {1}) {:} 3}$	${displaystyle (2 {ar {*}} 2_ {0} 2_ {1}) {:} 3}$
204			Я3	Я 2 / м 3	${displaystyle Gamma _ {c} ^ {v} T_ {h} ^ {5}}$	63 с	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight) cdot m / {ilde {6}}}$	${displaystyle 8 ^ {- circ}}$	${displaystyle [2_ {1} {*} {cdot} 2 {cdot} 2] {:} 3}$	${displaystyle [2_ {1} {*} {cdot} 2 {cdot} 2] {:} 3}$
205			Па3	П 2₁/ а 3	${displaystyle Gamma _ {c} T_ {h} ^ {6}}$	91a	${displaystyle left (a: a: aight) cdot {ilde {a}} / {ilde {6}}}$	${displaystyle 2 ^ {-} / 4}$	${displaystyle (2_ {1} 2 {ar {*}} {:}) {:} 3)}$	${displaystyle (2_ {1} 2 {ar {*}} {:}) {:} 3)}$
206			Я3	Я 2₁/ а 3	${displaystyle Gamma _ {c} ^ {v} T_ {h} ^ {7}}$	92а	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight) cdot {ilde {a}} / {ilde {6}}}$	${displaystyle 4 ^ {-} / 4}$	${displaystyle (* 2_ {1} 2 {:} 2 {:} 2) {:} 3}$	${displaystyle (* 2_ {1} 2 {:} 2 {:} 2) {:} 3}$
207	432	${displaystyle 432}$	P432	П 4 3 2	${displaystyle Gamma _ {c} O ^ {1}}$	68 с	${displaystyle left (a: a: aight): 4/3}$	${displaystyle 4 ^ {circ -}}$	${displaystyle (* 4_ {0} 4_ {0} 2_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 6}$
208			P4₂32	Стр. 4₂ 3 2	${displaystyle Gamma _ {c} O ^ {2}}$	98a	${displaystyle left (a: a: aight): 4_ {2} // 3}$	${displaystyle 4 ^ {+}}$	${displaystyle (* 4_ {2} 4_ {2} 2_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 6}$
209			F432	Ж 4 3 2	${displaystyle Gamma _ {c} ^ {f} O ^ {3}}$	70-е годы	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4/3 }$	${displaystyle 2 ^ {circ -}}$	${displaystyle (* 4_ {2} 4_ {0} 2_ {1}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 6}$
210			F4₁32	П 4₁ 3 2	${displaystyle Gamma _ {c} ^ {f} O ^ {4}}$	97a	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4_ {1 } // 3}$	${displaystyle 2 ^ {+}}$	${displaystyle (* 4_ {3} 4_ {1} 2_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 6}$
211			I432	Я 4 3 2	${displaystyle Gamma _ {c} ^ {v} O ^ {5}}$	69 с	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): 4/3}$	${displaystyle 8 ^ {+ circ}}$	${displaystyle (4_ {2} 4_ {0} 2_ {1}) {: 3}}$	${displaystyle (2_ {1} {*} 2_ {0} 2_ {0}) {:} 6}$
212			P4₃32	Стр. 4₃ 3 2	${displaystyle Gamma _ {c} O ^ {6}}$	94a	${displaystyle left (a: a: aight): 4_ {3} // 3}$	${displaystyle 2 ^ {+} / 4}$	${displaystyle (4_ {1} {*} 2_ {1}) {:} 3}$	${displaystyle (2_ {1} 2_ {1} {ar {imes}}) {:} 6}$
213			P4₁32	Стр. 4₁ 3 2	${displaystyle Gamma _ {c} O ^ {7}}$	95а	${displaystyle left (a: a: aight): 4_ {1} // 3}$	${displaystyle 2 ^ {+} / 4}$	${displaystyle (4_ {1} {*} 2_ {1}) {:} 3}$	${displaystyle (2_ {1} 2_ {1} {ar {imes}}) {:} 6}$
214			I4₁32	Я 4₁ 3 2	${displaystyle Gamma _ {c} ^ {v} O ^ {8}}$	96а	${displaystyle left ({frac {a + b + c} {2}} /: a: a: aight): 4_ {1} // 3}$	${displaystyle 4 ^ {+} / 4}$	${displaystyle (* 4_ {3} 4_ {1} 2_ {0}) {:} 3}$	${displaystyle (2_ {0} {*} 2_ {1} 2_ {1}) {:} 6}$
215	43м	${displaystyle * 332}$	п43м	п 4 3 мес.	${displaystyle Gamma _ {c} T_ {d} ^ {1}}$	65-е годы	${displaystyle left (a: a: aight): {ilde {4}} / 3}$	${displaystyle 2 ^ {circ} {:} 2}$	${displaystyle (* 4 {cdot} 42_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 6}$
216			F43м	F 4 3 мес.	${displaystyle Gamma _ {c} ^ {f} T_ {d} ^ {2}}$	67с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): {ilde { 4}} / 3}$	${displaystyle 1 ^ {circ} {:} 2}$	${displaystyle (* 4 {cdot} 42_ {1}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 6}$
217			я43м	я 4 3 мес.	${displaystyle Gamma _ {c} ^ {v} T_ {d} ^ {3}}$	66-е годы	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): {ilde {4}} / 3}$	${displaystyle 4 ^ {circ} {:} 2}$	${displaystyle (* {cdot} 44 {:} 2) {:} 3}$	${displaystyle (2_ {1} {*} 2_ {0} 2_ {0}) {:} 6}$
218			п43n	п 4 3 п	${displaystyle Gamma _ {c} T_ {d} ^ {4}}$	51ч	${displaystyle left (a: a: aight): {ilde {4}} // 3}$	${displaystyle 4 ^ {circ}}$	${displaystyle (* 4 {:} 42_ {0}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {0} 2_ {0} 2_ {0}) {:} 6}$
219			F43c	F 4 3 с	${displaystyle Gamma _ {c} ^ {f} T_ {d} ^ {5}}$	52ч	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): {ilde { 4}} // 3}$	${displaystyle 2 ^ {circ circ}}$	${displaystyle (* 4 {:} 42_ {1}) {:} 3}$	${displaystyle (* 2_ {0} 2_ {1} 2_ {0} 2_ {1}) {:} 6}$
220			я43D	я 4 3 дн.	${displaystyle Gamma _ {c} ^ {v} T_ {d} ^ {6}}$	93а	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): {ilde {4}} // 3}$	${displaystyle 4 ^ {circ} / 4}$	${displaystyle (4 {ar {*}} 2_ {1}) {:} 3}$	${displaystyle (2_ {0} {*} 2_ {1} 2_ {1}) {:} 6}$
221	4 / м 3 2 / м	${displaystyle * 432}$	Вечера3м	P 4 / м 3 2 / м	${displaystyle Gamma _ {c} O_ {h} ^ {1}}$	71-е годы	${displaystyle left (a: a: aight): 4 / {ilde {6}} cdot m}$	${displaystyle 4 ^ {-} {:} 2}$	${displaystyle [* {cdot} 4 {cdot} 4 {cdot} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2] {:} 6}$
222			Pn3п	P 4 / n 3 2 / п	${displaystyle Gamma _ {c} O_ {h} ^ {2}}$	53ч	${displaystyle left (a: a: aight): 4 / {ilde {6}} cdot {widetilde {abc}}}$	${displaystyle 8 ^ {circ circ}}$	${displaystyle (* 4_ {0} 4 {:} 2) {:} 3}$	${displaystyle (2 {ar {*}} _ {1} 2_ {0} 2_ {0}) {:} 6}$
223			Вечера3п	Стр. 4₂/ м 3 2 / п	${displaystyle Gamma _ {c} O_ {h} ^ {3}}$	102a	${displaystyle left (a: a: aight): 4_ {2} // {ilde {6}} cdot {widetilde {abc}}}$	${displaystyle 8 ^ {circ}}$	${displaystyle [* {cdot} 4 {:} 4 {cdot} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {cdot} 2 {cdot} 2] {:} 6}$
224			Pn3м	Стр. 4₂/ п 3 2 / м	${displaystyle Gamma _ {c} O_ {h} ^ {4}}$	103a	${displaystyle left (a: a: aight): 4_ {2} // {ilde {6}} cdot m}$	${displaystyle 4 ^ {+} {:} 2}$	${displaystyle (* 4_ {2} 4 {cdot} 2) {:} 3}$	${displaystyle (2 {ar {*}} _ {1} 2_ {0} 2_ {0}) {:} 6}$
225			FM3м	Ж 4 / м 3 2 / м	${displaystyle Gamma _ {c} ^ {f} O_ {h} ^ {5}}$	73 с	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4 / { ilde {6}} cdot m}$	${displaystyle 2 ^ {-} {:} 2}$	${displaystyle [* {cdot} 4 {cdot} 4 {:} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {:} 2 {:} 2] {:} 6}$
226			FM3c	Ж 4 / м 3 2 / с	${displaystyle Gamma _ {c} ^ {f} O_ {h} ^ {6}}$	54ч	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4 / { ilde {6}} cdot {ilde {c}}}$	${displaystyle 4 ^ {-}}$	${displaystyle [* {cdot} 4 {:} 4 {:} 2] {:} 3}$	${displaystyle [* {cdot} 2 {cdot} 2 {:} 2 {:} 2] {:} 6}$
227			Fd3м	П 4₁/ д 3 2 / м	${displaystyle Gamma _ {c} ^ {f} O_ {h} ^ {7}}$	100а	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4_ {1 } // {ilde {6}} cdot m}$	${displaystyle 2 ^ {+} {:} 2}$	${displaystyle (* 4_ {1} 4 {cdot} 2) {:} 3}$	${displaystyle (2 {ar {*}} 2_ {0} 2_ {1}) {:} 6}$
228			Fd3c	П 4₁/ д 3 2 / с	${displaystyle Gamma _ {c} ^ {f} O_ {h} ^ {8}}$	101а	${displaystyle left ({frac {a + c} {2}} / {frac {b + c} {2}} / {frac {a + b} {2}}: a: a: aight): 4_ {1 } // {ilde {6}} cdot {ilde {c}}}$	${displaystyle 4 ^ {++}}$	${displaystyle (* 4_ {1} 4 {:} 2) {:} 3}$	${displaystyle (2 {ar {*}} 2_ {0} 2_ {1}) {:} 6}$
229			Я3м	Я 4 / м 3 2 / м	${displaystyle Gamma _ {c} ^ {v} O_ {h} ^ {9}}$	72-е	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): 4 / {ilde {6}} cdot m}$	${displaystyle 8 ^ {circ} {:} 2}$	${displaystyle [* {cdot} 4 {cdot} 4 {:} 2] {:} 3}$	${displaystyle [2_ {1} {*} {cdot} 2 {cdot} 2] {:} 6}$
230			Я3d	Я 4₁/ а 3 2 / д	${displaystyle Gamma _ {c} ^ {v} O_ {h} ^ {10}}$	99a	${displaystyle left ({frac {a + b + c} {2}} / a: a: aight): 4_ {1} // {ilde {6}} cdot {frac {1} {2}} {widetilde { abc}}}$	${displaystyle 8 ^ {circ} / 4}$	${displaystyle (* 4_ {1} 4 {:} 2) {:} 3}$	${displaystyle (* 2_ {1} 2 {:} 2 {:} 2) {:} 6}$

использованная литература

^ Bradley, C.J .; Кракнелл, А. П. (2010). Математическая теория симметрии в твердых телах: теория представлений для точечных групп и пространственных групп. Оксфорд, Нью-Йорк: Кларендон Пресс. С. 127–134. ISBN 978-0-19-958258-7. OCLC 859155300.

внешняя ссылка

[1] Bradley, C.J .; Кракнелл, А. П. (2010). Математическая теория симметрии в твердых телах: теория представлений для точечных групп и пространственных групп. Оксфорд, Нью-Йорк: Кларендон Пресс. С. 127–134. ISBN 978-0-19-958258-7. OCLC 859155300.

[1]