Матроидный многогранник - Matroid polytope

В математике матроидный многогранник, также называемый матроидный базисный многогранник (или же базисный матроидный многогранник), чтобы отличить его от других многогранников, производных от матроида, является многогранник построенный по базам матроид. Учитывая матроид ${ displaystyle M}$, матроидный многогранник ${ displaystyle P_ {M}}$ это выпуклый корпус из индикаторные векторы основ ${ displaystyle M}$.

Определение

Позволять ${ displaystyle M}$ быть матроид на ${ displaystyle n}$ элементы. Учитывая основу ${ Displaystyle B substeq {1, точки, п }}$ из ${ displaystyle M}$, то индикаторный вектор из ${ displaystyle B}$ является

${ displaystyle mathbf {e} _ {B}: = sum _ {i in B} mathbf {e} _ {i},}$

куда ${ Displaystyle mathbf {е} _ {я}}$ это стандарт ${ displaystyle i}$й единичный вектор в ${ Displaystyle mathbb {R} ^ {п}}$. В матроидный многогранник ${ displaystyle P_ {M}}$ это выпуклый корпус из набора

${ displaystyle { mathbf {e} _ {B} mid B { text {является основой}} M } substeq mathbb {R} ^ {n}.}$

Примеры

Квадратная пирамида

Октаэдр

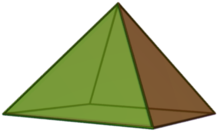
• Позволять ${ displaystyle M}$ - матроид ранга 2 на 4 элементах с базами

${ Displaystyle { mathcal {B}} (М) = { {1,2 }, {1,3 }, {1,4 }, {2,3 }, { 2,4 } }.}$

То есть все 2-элементные подмножества ${ displaystyle {1,2,3,4 }}$ Кроме ${ displaystyle {3,4 }}$. Соответствующие индикаторные векторы ${ Displaystyle { mathcal {B}} (М)}$ находятся

${ Displaystyle { {1,1,0,0 }, {1,0,1,0 }, {1,0,0,1 }, {0,1,1,0 }, {0,1,0,1 } }.}$

Матроидный многогранник ${ displaystyle M}$ является

${ Displaystyle P_ {M} = { text {conv}} { {1,1,0,0 }, {1,0,1,0 }, {1,0,0,1 }, {0,1,1,0 }, {0,1,0,1 } }.}$

Эти точки образуют четыре равносторонние треугольники в точке ${ displaystyle {1,1,0,0 }}$, поэтому его выпуклая оболочка квадратная пирамида по определению.

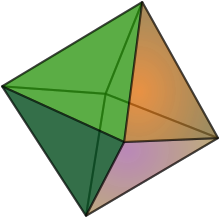
• Позволять ${ displaystyle N}$ - матроид ранга 2 на 4 элементах с основаниями все 2-элементные подмножества ${ displaystyle {1,2,3,4 }}$. Соответствующий матроидный многогранник ${ Displaystyle P_ {N}}$ это октаэдр. Заметим, что многогранник ${ displaystyle P_ {M}}$ из предыдущего примера содержится в ${ Displaystyle P_ {N}}$.
• Если ${ displaystyle M}$ это униформа матроид ранга ${ displaystyle r}$ на ${ displaystyle n}$ элементов, то матроидный многогранник ${ displaystyle P_ {M}}$ это гиперсимплекс ${ displaystyle Delta _ {n} ^ {r}}$.^[1]

Характеристики

• Матроидный многогранник содержится в гиперсимплекс ${ displaystyle Delta _ {n} ^ {r}}$, куда ${ displaystyle r}$ - ранг ассоциированного матроида и ${ displaystyle n}$ - размер основного набора связанного матроида.^[2] Более того, вершины ${ displaystyle P_ {M}}$ являются подмножеством вершин ${ displaystyle Delta _ {n} ^ {r}}$.
• Каждое ребро матроидного многогранника ${ displaystyle P_ {M}}$ параллельный перевод ${ displaystyle e_ {i} -e_ {j}}$ для некоторых ${ displaystyle i, j in E}$, основной набор связанного матроида. Другими словами, края ${ displaystyle P_ {M}}$ точно соответствуют парам оснований ${ displaystyle B, B '}$ которые удовлетворяют базисная обменная собственность: ${ displaystyle B '= B setminus {я чашка j}}$ для некоторых ${ displaystyle i, j in E.}$^[2] Благодаря этому свойству длина каждой кромки равна квадратный корень из двух. В более общем смысле, семейства множеств, для которых выпуклая оболочка индикаторных векторов имеет длину ребер один или квадратный корень из двух, в точности являются дельта-матроиды.
• Матроидные многогранники являются членами семейства обобщенные пермутоэдры.^[3]
• Позволять ${ displaystyle r: 2 ^ {E} rightarrow mathbb {Z}}$ - ранговая функция матроида ${ displaystyle M}$. Матроидный многогранник ${ displaystyle P_ {M}}$ можно записать однозначно как подписанный Сумма Минковского из симплексы:^[3]

${ Displaystyle P_ {M} = sum _ {A substeq E} { tilde { beta}} (M / A) Delta _ {E-A}}$

куда ${ displaystyle E}$ основной набор матроида ${ displaystyle M}$ и ${ Displaystyle бета (М)}$ знаковый бета-инвариант ${ displaystyle M}$:

${ Displaystyle { тильда { бета}} (М) = (- 1) ^ {г (М) +1} бета (М),}$

${ Displaystyle бета (M) = (- 1) ^ {r (M)} sum _ {X substeq E} (- 1) ^ {| X |} r (X).}$

${ Displaystyle P_ {M}: = left {{ textbf {x}} in mathbb {R} _ {+} ^ {E} ~ | ~ sum _ {e in U} { textbf {x}} (e) leq r (U), forall U substeq E right }}$

Связанные многогранники

Матроидный многогранник независимости

В Матроидный многогранник независимости или же Матроидный многогранник независимости выпуклая оболочка множества

${ displaystyle {, mathbf {e} _ {I} mid I { text {является независимым набором}} M , } substeq mathbb {R} ^ {n}.}$

Матроидный (базисный) многогранник является гранью матроидного многогранника независимости. Учитывая классифицировать ${ displaystyle psi}$ матроида ${ displaystyle M}$, многогранник матроид независимости равен полиматроид определяется по ${ displaystyle psi}$.

Пометить матроидный многогранник

Матроидный многогранник флага - еще один многогранник, построенный из основ матроидов. А флаг ${ Displaystyle { mathcal {F}}}$ строго возрастающая последовательность

${ Displaystyle F ^ {1} подмножество F ^ {2} subset cdots subset F ^ {m} ,}$

конечных множеств.^[4] Позволять ${ displaystyle k_ {i}}$ - мощность множества ${ displaystyle F_ {i}}$. Два матроида ${ displaystyle M}$ и ${ displaystyle N}$ как говорят согласный если их ранговые функции удовлетворяют

${ Displaystyle r_ {M} (Y) -r_ {M} (X) leq r_ {N} (Y) -r_ {N} (X) { text {для всех}} X subset Y substeq E . ,}$

Даны попарно согласованные матроиды ${ displaystyle M_ {1}, dots, M_ {m}}$ на земле установлен ${ displaystyle E}$ со званиями ${ displaystyle r_ {1} < cdots$, рассмотрим набор флагов ${ displaystyle (B_ {1}, dots, B_ {m})}$ куда ${ displaystyle B_ {i}}$ является основой матроида ${ displaystyle M_ {i}}$ и ${ Displaystyle B_ {1} subset cdots subset B_ {m}}$. Такой набор флагов - это флаг матроид ${ Displaystyle { mathcal {F}}}$. Матроиды ${ displaystyle M_ {1}, dots, M_ {m}}$ называются составляющие из ${ Displaystyle { mathcal {F}}}$.Для каждого флага ${ displaystyle B = (B_ {1}, dots, B_ {m})}$ в матроиде флага ${ Displaystyle { mathcal {F}}}$, позволять ${ displaystyle v_ {B}}$ быть суммой индикаторных векторов каждого базиса в ${ displaystyle B}$

${ Displaystyle v_ {B} = v_ {B_ {1}} + cdots + v_ {B_ {m}}. ,}$

Учитывая матроид флага ${ Displaystyle { mathcal {F}}}$, то флаг матроид многогранник ${ Displaystyle P _ { mathcal {F}}}$ выпуклая оболочка множества

${ displaystyle {v_ {B} mid B { text {- это флаг в}} { mathcal {F}} }.}$

Матроидный многогранник флага может быть записан как сумма Минковского (базисных) матроидных многогранников составляющих матроид:^[4]

${ Displaystyle P _ { mathcal {F}} = P_ {M_ {1}} + cdots + P_ {M_ {k}}. ,}$

Рекомендации