Машина Мура - Википедия - Moore machine

в теория вычислений, а Машина Мура это конечный автомат чьи выходные значения определяются только его текущим государственный. Это в отличие от Мучная машина, чьи (Мили) выходные значения определяются как его текущим состоянием, так и значениями его входов. Машина Мура названа в честь Эдвард Ф. Мур, который представил концепцию в статье 1956 года, «Геданкен-эксперименты на последовательных машинах ».^[1]

Формальное определение

Машину Мура можно определить как 6-кратный ${ displaystyle (Q, q_ {0}, Sigma, O, delta, G)}$ состоящий из следующего:

Конечный набор состояния ${ displaystyle Q}$
Начальное состояние (также называемое начальным состоянием) ${ displaystyle q_ {0}}$ который является элементом ${ displaystyle Q}$
Конечное множество, называемое входом алфавит ${ displaystyle Sigma}$
Конечное множество, называемое выходом алфавит ${ displaystyle O}$
Переход функция ${ displaystyle delta: Q times Sigma rightarrow Q}$ отображение состояния и входного алфавита на следующее состояние
Функция вывода ${ displaystyle G: Q rightarrow O}$ отображение каждого состояния в выходной алфавит

Машину Мура можно рассматривать как ограниченный тип конечный преобразователь.

Визуальное представление

Стол

Таблица перехода состояний - таблица, показывающая связь между вводом и состоянием.^{[требуется разъяснение ]}

Диаграмма

В диаграмма состояний для машины Мура или диаграммы Мура - это диаграмма, которая связывает выходное значение с каждым состоянием. Машина Мура является производителем выходных данных.

Связь с машинами Мили

Поскольку машины Мура и Мили являются типами конечных автоматов, они одинаково выразительны: любой тип может использоваться для анализа обычный язык.

Разница между машинами Мура и Мучные машины состоит в том, что в последнем случае выход перехода определяется комбинацией текущих государственный и текущий ввод ( ${ Displaystyle S times Sigma}$ как вход в ${ displaystyle G}$ ), а не только текущее состояние ( ${ displaystyle S}$ как вход в ${ displaystyle G}$ ). Когда он представлен как диаграмма состояний,

для машины Мура каждый узел (состояние) помечен выходным значением;
для машины Мили каждая дуга (переход) помечена выходным значением.

Каждая машина Мура ${ displaystyle M}$ эквивалентна машине Мили с теми же состояниями и переходами, а функция вывода ${ Displaystyle G (s, sigma) rightarrow G_ {M} ( delta _ {M} (s, sigma))}$ , который принимает каждую пару состояние-вход ${ displaystyle (s, sigma)}$ и дает ${ Displaystyle G_ {M} ( delta _ {M} (s, sigma))}$ , куда ${ displaystyle G_ {M}}$ является ${ displaystyle M}$ функция вывода и ${ displaystyle delta _ {M}}$ является ${ displaystyle M}$ функция перехода.

Однако не каждую машину Мили можно преобразовать в эквивалентную машину Мура. Некоторые могут быть преобразованы только в почти эквивалентная машина Мура, со смещенными во времени выходами. Это связано с тем, что метки состояния соединяются с метками перехода для формирования пар ввода / вывода. Рассмотрим переход ${ displaystyle s_ {i} rightarrow s_ {j}}$ от государства ${ displaystyle s_ {i}}$ заявить ${ displaystyle s_ {j}}$ . Вход, вызывающий переход ${ displaystyle s_ {i} rightarrow s_ {j}}$ маркирует край ${ displaystyle (s_ {i}, s_ {j})}$ . Выход, соответствующий этому входу, является меткой состояния ${ displaystyle s_ {i}}$ .^[2] Обратите внимание, что это исходное состояние перехода. Таким образом, для каждого входа выход уже фиксирован до того, как вход получен, и зависит исключительно от текущего состояния. Это первоначальное определение Э. Мура. Использование ярлыка состояния - распространенная ошибка. ${ displaystyle s_ {j}}$ как выход для перехода ${ displaystyle s_ {i} rightarrow s_ {j}}$ .

Примеры

Типы по количеству входов / выходов.

Простой

Простые машины Мура имеют один вход и один выход:

детектор края с помощью XOR
двоичная суммирующая машина
синхронизированные последовательные системы (ограниченная форма машины Мура, где состояние изменяется только при изменении глобального тактового сигнала)

Большинство цифровых электронных систем разработаны как синхронизированные последовательные системы. Тактовые последовательные системы - это ограниченная форма машины Мура, где состояние изменяется только при изменении глобального тактового сигнала. Обычно текущее состояние хранится в шлепки, а глобальный тактовый сигнал подключается ко входу «тактового сигнала» триггеров. Тактовые последовательные системы - один из способов решения метастабильность проблемы. Типичная электронная машина Мура включает комбинационная логика цепочка для декодирования текущего состояния в выходы (лямбда). В тот момент, когда изменяется текущее состояние, эти изменения проходят через эту цепочку, и почти мгновенно вывод обновляется. Существуют методы проектирования, гарантирующие, что глюки происходят на выходах в течение этого короткого периода, пока эти изменения распространяются по цепочке, но большинство систем спроектировано так, что сбои в течение этого короткого времени перехода игнорируются или не имеют значения. Затем выходы остаются неизменными бесконечно (Светодиоды оставаться ярким, питание остается подключенным к двигателям, соленоиды оставаться под напряжением и т. д.), пока машина Мура снова не изменит состояние.

Пример работы

Последовательная сеть имеет один вход и один выход. Выход становится 1 и остается 1 после этого, когда по крайней мере два нуля и две единицы встречаются в качестве входных данных.

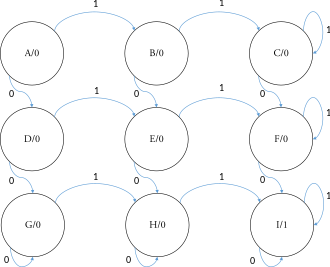
Пример мур-машины

Справа показана машина с девятью состояниями для приведенного выше описания. Начальное состояние - состояние A, а конечное состояние - состояние I. Таблица состояний для этого примера выглядит следующим образом:

Текущее состояние	Вход	Следующее состояние	Выход
А	0	D	0
А	1	B	0
B	0	E	0
B	1	C	0
C	0	F	0
C	1	C	0
D	0	грамм	0
D	1	E	0
E	0	ЧАС	0
E	1	F	0
F	0	я	0
F	1	F	0
грамм	0	грамм	0
грамм	1	ЧАС	0
ЧАС	0	ЧАС	0
ЧАС	1	я	0
я	0	я	1
я	1	я	1

Сложный

Более сложные машины Мура могут иметь несколько входов, а также несколько выходов.

Геданкен-эксперименты

В статье Мура "Геданкен-эксперименты на последовательных машинах »,^[1] то ${ Displaystyle (п; м; р)}$ автоматы (или машины) ${ displaystyle S}$ определяются как имеющие ${ displaystyle n}$ состояния, ${ displaystyle m}$ входные символы и ${ displaystyle p}$ выходные символы. Доказаны девять теорем о строении ${ displaystyle S}$ , и эксперименты с ${ displaystyle S}$ . Потом, " ${ displaystyle S}$ машины »стали называть« машинами Мура ».

В конце статьи, в разделе «Дальнейшие проблемы», ставится следующая задача:

Другая непосредственно следующая проблема - это улучшение оценок, приведенных в теоремах 8 и 9.

Теорема Мура 8 сформулирована следующим образом:

Учитывая произвольную ${ Displaystyle (п; м; р)}$ машина ${ displaystyle S}$ , такое, что каждые два его состояния отличимы друг от друга, то существует эксперимент длины ${ Displaystyle { tfrac {п (п-1)} {2}}}$ что определяет состояние ${ displaystyle S}$ в конце эксперимента.

В 1957 г. А. А. Карацуба доказал следующие две теоремы, полностью решившие проблему Мура об улучшении оценок длины эксперимента его «Теоремы 8».

Теорема А. Если ${ displaystyle S}$ является ${ Displaystyle (п; м; р)}$ машина такая, что каждые два ее состояния отличимы друг от друга, то существует разветвленный эксперимент продолжительностью не более ${ Displaystyle { tfrac {(п-1) (п-2)} {2}} + 1}$ по которому можно определить состояние ${ displaystyle S}$ в конце эксперимента.

Теорема Б. Существует ${ Displaystyle (п; м; р)}$ машины, каждые два состояния которой различимы друг от друга, так что продолжительность кратчайших экспериментов, устанавливающих состояние машины в конце эксперимента, равна ${ Displaystyle { tfrac {(п-1) (п-2)} {2}} + 1}$ .

Теоремы А и Б легли в основу курсовой работы студента четвертого курса Карацубы А.А. «К задаче из теории автоматов», которая была отмечена отзывом на конкурсе студенческих работ факультета механики и математики МГУ им. М.В. Ломоносова в 1958 г. Статья Карацубы передана в журнал. Успехи матем. Наук 17 декабря 1958 г. и был опубликован там в июне 1960 г.^[3]

До настоящего времени (2011 г.) результат Карацубы о продолжительности экспериментов является единственным точным нелинейным результатом как в теории автоматов, так и в аналогичных задачах теории сложности вычислений.

Смотрите также

дальнейшее чтение

Конвей, Дж. (1971). Регулярная алгебра и конечные машины. Лондон: Чепмен и Холл. ISBN 0-412-10620-5. Zbl 0231.94041.
Мур Э. Ф. Геданкен-эксперименты на последовательных машинах. Исследования автоматов, Анналы математических исследований, 34, 129–153. Издательство Принстонского университета, Принстон, Нью-Джерси (1956).
Карацуба А. А. Решение одной задачи теории конечных автоматов. Усп. Мат. 1960. Т. 15: 3. С. 157–159.
Карацуба А. А. Experimente mit Automaten (нем.) Elektron. Информация Кибернетик, 11, 611–612 (1975).
Карацуба А.А. Список исследовательских работ.

Машина Мура и Мили

внешняя ссылка

СМИ, связанные с Машина Мура в Wikimedia Commons

[gedanken-1] а ^б Мур, Эдвард Ф (1956). «Геданкен-эксперименты на последовательных машинах». Исследования автоматов, Анналы математических исследований. Принстон, Нью-Джерси: Издательство Принстонского университета (34): 129–153.

[2] Ли, Эдвард Эшфорд; Сешия, Санджит Арункумар (2013). Введение во встраиваемые системы (1.08 ред.). Калифорнийский университет в Беркли: Lulu.com. ISBN 9780557708574. Получено 1 июля 2014.

[3] Карацуба, А.А. (1960). «Решение одной задачи из теории конечных автоматов». Успехи матем. Наук (15:3): 157–159.

[1]

[2]

[3]