Числовая точность в Microsoft Excel - Википедия - Numeric precision in Microsoft Excel
Как и в случае с другими таблицами, Майкрософт Эксель работает только с ограниченной точностью, потому что сохраняет только определенное количество цифр для описания чисел (он ограничен точность ). За некоторыми исключениями, касающимися ошибочных значений, бесконечностей и денормализованных чисел, Excel вычисляет в формат с плавающей запятой двойной точности от Спецификация IEEE 754[1] (помимо чисел Excel использует еще несколько типов данных[2]). Хотя Excel может отображать 30 знаков после запятой, его точность для указанного числа ограничена 15. значимые фигуры, а точность расчетов может быть еще меньше из-за трех проблем: округлять,[3] усечение, и двоичное хранилище.
Точность и двоичная память


На верхнем рисунке отображается дробь 1/9000 в Excel. Хотя это число имеет десятичное представление, представляющее собой бесконечную строку единиц, Excel отображает только первые 15 цифр. Во второй строке к дроби добавляется цифра один, и снова Excel отображает только 15 цифр. В третьей строке вычитается единица из суммы с помощью Excel. Поскольку в сумме после десятичной дроби всего одиннадцать единиц, истинная разница при вычитании «1» составляет три нуля, за которыми следует строка из одиннадцати единиц. Однако разница, о которой сообщает Excel, составляет три нуля, за которыми следует 15-значная строка тринадцать 1 и две лишние ошибочные цифры. Таким образом, Excel вычисляет числа: нет числа, которые он отображает. Более того, ошибка в ответе Excel - это не просто ошибка округления.
Неточность расчетов в Excel сложнее ошибок из-за точности до 15 значащих цифр. Хранение чисел в двоичном формате Excel также влияет на его точность.[4] Для иллюстрации на нижнем рисунке приведено простое добавление 1 + Икс − 1 для нескольких значений Икс. Все ценности Икс начинаются с 15-го десятичного знака, поэтому Excel должен их учитывать. Перед подсчетом суммы 1 + Икс, Excel в первом приближении Икс как двоичное число. Если эта двоичная версия Икс представляет собой простую степень двойки, 15-значное десятичное приближение к Икс хранится в сумме, а два верхних примера на рисунке указывают на восстановление Икс без ошибок. В третьем примере Икс более сложное двоичное число, Икс = 1.110111⋯111 × 2−49 (Всего 15 бит). Здесь Икс аппроксимируется 4-битным двоичным кодом 1.111 × 2−49 (некоторое представление об этом приближении можно найти, используя геометрическая прогрессия: Икс = 1.11 × 2−49 + 2−52 × (1 − 2−11) ≈ 1.11 × 2−49 + 2−52 = 1.111 × 2−49 ) и используется десятичный эквивалент этого грубого 4-битного приближения. В четвертом примере Икс это десятичный число, не эквивалентное простому двоичному файлу (хотя оно согласуется с двоичным кодом третьего примера относительно отображаемой точности). Десятичный ввод аппроксимируется двоичным, а затем который используется десятичная дробь. Эти два средних примера на рисунке показывают, что вносится некоторая ошибка.
Последние два примера показывают, что произойдет, если Икс это довольно небольшое число. Во втором из последнего примера Икс = 1.110111⋯111 × 2−50; Всего 15 бит. двоичный файл очень грубо заменяется одной степенью двойки (в этом примере 2−49) и его десятичный эквивалент. В нижнем примере десятичная дробь, идентичная двоичной системе с указанной выше точностью, тем не менее, аппроксимируется иначе, чем двоичная, и исключается путем усечения до 15 значащих цифр, не влияя на 1 + Икс − 1, что приводит к Икс = 0.[5]
За Икс'S, которые не являются простой степенью двойки, заметная ошибка в 1 + Икс − 1 может произойти даже тогда, когда Икс довольно большой. Например, если Икс = 1/1000, тогда 1 + Икс − 1 = 9.9999999999989 × 10−4, ошибка в 13-й значащей цифре. В этом случае, если бы Excel просто добавлял и вычитал десятичные числа, избегая преобразования в двоичное и обратно в десятичное, ошибки округления не возникало бы, и точность фактически была бы лучше. В Excel есть опция «Установить точность как отображаемую».[6] С помощью этого параметра, в зависимости от обстоятельств, точность может быть лучше или хуже, но вы будете точно знать, что делает Excel. (Следует отметить, однако, что сохраняется только выбранная точность, и нельзя восстановить дополнительные цифры, изменив эту опцию.) Некоторые аналогичные примеры можно найти по этой ссылке.[7]
Короче говоря, разнообразие поведения точности вводится комбинацией представления числа с ограниченным количеством двоичных цифр вместе с усечение числа после пятнадцатой значащей цифры.[8] Обработка в Excel чисел, превышающих 15 значащих цифр, иногда способствует большей точности последних нескольких значащих цифр в вычислении, чем прямая работа только с 15 значащими цифрами, а иногда и нет.
Обоснование преобразования в двоичное представление и обратно в десятичное, а также дополнительные сведения о точности в Excel и VBA см. По этим ссылкам.[9]
Примеры, в которых точность не является показателем точности
Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Апрель 2010 г.) |
Статистические функции
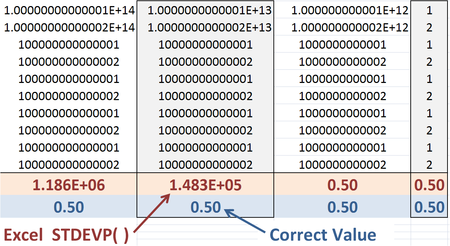
Точность функций, предоставляемых Excel, может быть проблемой. Мика Альтман и другие. представьте этот пример:[10] Стандартное отклонение совокупности, определяемое как:
математически эквивалентно:
Однако первая форма сохраняет лучшую численную точность для больших значений Икс, потому что квадраты разностей между Икс и Икссредний приводит к меньшему округлению, чем разница между гораздо большими числами Σx2 и (Σx)2. Однако встроенная функция Excel STDEVP () использует менее точную формулировку, поскольку она быстрее в вычислительном отношении.[11]
И функция «совместимости» STDEVP, и функция «согласованности» STDEV.P в Excel 2010 возвращают стандартное отклонение генеральной совокупности 0,5 для заданного набора значений. Тем не менее, численную неточность все же можно показать на этом примере, расширив существующий рисунок, включив 1015, после чего ошибочное стандартное отклонение, обнаруженное Excel 2010, будет равно нулю.
Вычитание результатов вычитания
Выполнение простых вычитаний может привести к ошибкам, так как две ячейки могут отображать одно и то же числовое значение при сохранении двух отдельных значений. Пример этого происходит на листе, где следующие ячейки имеют следующие числовые значения:
и следующие ячейки содержат следующие формулы
Обе клетки и отображать . Однако если ячейка содержит формулу тогда не отображает как и следовало ожидать, но отображает вместо.
Ошибка округления
Пользовательские вычисления должны быть тщательно организованы, чтобы ошибка округления не стала проблемой. Пример возникает при решении квадратное уровненеие:
Решения (корни) этого уравнения точно определяются квадратичная формула:
Когда один из этих корней очень велик по сравнению с другим, то есть когда квадратный корень близок к значению б, оценка корня, соответствующего вычитанию двух членов, становится очень неточной из-за округления.
Можно определить ошибку округления, используя Серия Тейлор формула квадратного корня:[12]
Как следствие,
указывая, что, как б становится больше, первый оставшийся член, скажем, ε:
становится все меньше и меньше. Цифры для б и квадратный корень становится почти таким же, и разница становится небольшой:
В этих условиях все значащие цифры выражают б. Например, если точность составляет 15 цифр, и эти два числа, б и квадратный корень одинаковы для 15 цифр, вместо разницы ε разность будет равна нулю.
Лучшую точность можно получить с помощью другого подхода, описанного ниже.[13] Если обозначить два корня через р 1 и р 2, квадратное уравнение можно записать:
Когда корень р 1 >> р 2, сумма (р 1 + р 2 ) ≈ р 1 и сравнение двух форм показывает примерно:
пока
Таким образом, находим примерный вид:
Эти результаты не подлежат ошибке округления, но они не точны, если б2 большой по сравнению сac.

Суть в том, что при выполнении этого расчета с использованием Excel, поскольку значения корней становятся все дальше друг от друга, метод расчета должен будет переключиться с прямого вычисления квадратной формулы на какой-либо другой метод, чтобы ограничить ошибку округления. Точка переключения методов зависит от размера коэффициентов. а иб.
На рисунке Excel используется для нахождения наименьшего корня квадратного уравнения. Икс2 + bx + c = 0 для c = 4 иc = 4 × 105. Разница между прямой оценкой с использованием формулы квадратиков и приближением, описанным выше для широко разнесенных корней, нанесена на график. против. б. Первоначально разница между методами уменьшается, потому что метод широко разнесенного корня становится более точным при увеличении б-значения. Однако помимо некоторых б-значение разница увеличивается, потому что квадратная формула (подходит для меньших б-значения) становится хуже из-за округления, в то время как метод широко разнесенного корня (подходит для больших б-значения) продолжает улучшаться. Точка переключения методов обозначена большими точками, и тем больше, чем больше c-значения. В целом б-значения, наклонная вверх кривая представляет собой ошибку округления Excel в квадратной формуле, неустойчивое поведение которой приводит к изгибу кривых.
Другая область, где точность является проблемой, - это область численный расчет интегралов и решение дифференциальных уравнений. Примеры Правило Симпсона, то Метод Рунге – Кутты, а алгоритм Нумерова для Уравнение Шредингера.[14] Используя Visual Basic для приложений, любой из этих методов можно реализовать в Excel. В численных методах используется сетка, в которой вычисляются функции. Функции могут быть интерполированы между точками сетки или экстраполированы для определения местоположения соседних точек сетки. Эти формулы включают сравнение соседних значений. Если сетка разнесена очень мелко, произойдет ошибка округления, и чем меньше используется точность, тем хуже ошибка округления. При большом расстоянии пострадает точность. Если представить себе численную процедуру как система обратной связи, этот вычислительный шум можно рассматривать как сигнал, который подается в систему, что приведет к нестабильности, если система не будет тщательно спроектирована.[15]
Точность в VBA
Хотя Excel номинально работает с 8 байт числа по умолчанию, VBA имеет множество типов данных. В Двойной тип данных - 8 байт, Целое число тип данных - 2 байта, а общий 16 байт Вариант тип данных может быть преобразован в 12-байтовый Десятичный тип данных с использованием функции преобразования VBA CDec.[16] Выбор типов переменных при вычислении VBA требует учета требований к памяти, точности и скорости.
Рекомендации
- ^ «Арифметика с плавающей запятой может давать неточные результаты в Excel». Редакция 8.2; Идентификатор статьи: 78113. Поддержка Microsoft. 30 июня 2010 г.. Получено 2010-07-02.
- ^ Стив Далтон (2007). «Таблица 2.3: Типы и ограничения данных рабочего листа». Финансовые приложения с использованием разработки надстроек Excel на C / C ++ (2-е изд.). Вайли. С. 13–14. ISBN 0-470-02797-5.
- ^ Округление - это потеря точности при вычитании чисел, различающихся на небольшую величину. Поскольку каждое число состоит только из пятнадцати значащих цифр, их разница будет неточной, если не будет достаточно значащих цифр, чтобы выразить разницу.
- ^ Роберт де Леви (2004). «Алгоритмическая точность». Расширенный Excel для анализа научных данных. Издательство Оксфордского университета. п. 44. ISBN 0-19-515275-1.
- ^ Чтобы ввести число в двоичном формате, оно представляется как строка степеней двойки: 2 ^ (- 50) * (2 ^ 0 + 2 ^ −1 + ⋯). Чтобы ввести число как десятичное, десятичное число вводится напрямую.
- ^ Этот параметр находится на вкладке «Параметры Excel / Дополнительно». Видеть Как исправить ошибки округления: метод 2
- ^ Странность сложения Excel
- ^ Роберт де Леви (2004). цитируемая работа. С. 45–46. ISBN 0-19-515275-1.
- ^ Точность в Excel:
- Арифметика с плавающей запятой может давать неточные результаты: Подробное объяснение с примерами последствий хранения двоичных / 15 сигнатур.
- Почему Excel дает неправильные ответы? В архиве 2010-03-30 на Wayback Machine: Еще одно подробное обсуждение с примерами и некоторыми исправлениями.
- Что должен знать каждый компьютерный ученый о плавающей запятой Сосредоточен на примерах представления чисел с плавающей запятой.
- Визуальная базовая и арифметическая точность: Ориентирован на VBA, который работает несколько иначе.
- Бернар В. Лиенгме (2008). «Математические ограничения Excel». Руководство по Microsoft Excel 2007 для ученых и инженеров. Академическая пресса. п. 31 год ff. ISBN 0-12-374623-X.
- ^ Мика Альтман; Джефф Гилл; Майкл Макдональд (2004). «§2.1.1 Показательный пример: вычисление стандартного отклонения коэффициента». Численные вопросы в статистических вычислениях для социолога. Wiley-IEEE. п. 12. ISBN 0-471-23633-0.
- ^ Роберт де Леви (2004). Расширенный Excel для анализа научных данных. Издательство Оксфордского университета. С. 45–46. ISBN 0-19-515275-1.
- ^ Градштейн Израиль Соломонович; Рыжик Иосиф Моисеевич; Геронимус Юрий Вениаминович; Цейтлин Михаил Юльевич; Джеффри, Алан (2015) [октябрь 2014]. «1.112. Силовой ряд». В Цвиллингере, Даниэль; Молл, Виктор Гюго (ред.). Таблица интегралов, серий и продуктов. Перевод Scripta Technica, Inc. (8-е изд.). Academic Press, Inc. п. 25. ISBN 0-12-384933-0. LCCN 2014010276.
- ^ Этот приближенный метод часто используется при проектировании усилителей с обратной связью, где два корня представляют время отклика системы. См. Статью о пошаговая реакция.
- ^ Андерс Блом Компьютерные алгоритмы решения уравнений Шредингера и Пуассона, Факультет физики Лундского университета, 2002 г.
- ^ Р. В. Хэмминг (1986). Численные методы для ученых и инженеров (2-е изд.). Courier Dover Publications. ISBN 0-486-65241-6. В этой книге подробно обсуждаются округление, усечение и стабильность. Например, см. Главу 21: Неопределенные интегралы - обратная связь, стр. 357.
- ^ Джон Уокенбах (2010). «Определение типов данных». Программирование Power в Excel 2010 с помощью VBA. Вайли. стр.198 ff и Таблица 8-1. ISBN 0-470-47535-8.

![{ sqrt {{ frac { Sigma (x - { bar {x}}) ^ {2}} {n}}}} = { sqrt {{ frac { Sigma left [x- left] ( Sigma x right) / n right] ^ {2}} {n}}}} ,](https://wikimedia.org/api/rest_v1/media/math/render/svg/fba9fcca2fb68488422af6749b3eaed03fb48865)






















