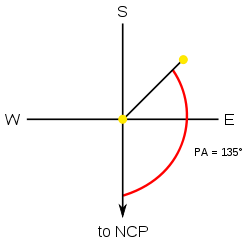
Иллюстрация того, как оценивается позиционный угол через окуляр телескопа; главная звезда находится в центре.
В астрономия, позиционный угол (обычно сокращенно PA) - это соглашение об измерении углов на небе. В Международный астрономический союз определяет его как угол, измеренный относительно северный полюс мира (NCP), превращаясь в положительную сторону прямое восхождение. В стандартных (не перевернутых) изображениях это счетчикпо часовой стрелке Измерьте относительно оси в направлении положительного склонение.
В случае наблюдаемого визуальные двойные звезды, он определяется как угловое смещение вторичной звезды от главной относительно северный полюс мира.
Как показывает пример, если бы кто-то наблюдал гипотетическую двойную звезду с PA 135 °, это означает, что воображаемая линия в окуляре, проведенная от северного небесного полюса к главному полюсу (P), будет смещена относительно вторичной звезды (S), так что что угол NCP-PS будет 135 °.
При построении визуальных орбит двоичных объектов линия NCP традиционно проводится вниз, то есть с севером внизу, а PA измеряется против часовой стрелки. Также направление собственное движение может, например, быть задан его позиционным углом.
Определение позиционного угла также применяется к протяженным объектам, таким как галактики, где он относится к углу, составляющему большую ось объекта с линией NCP.
Морское дело
Концепция позиционного угла унаследована от морской навигации по океанам, где оптимальные компас курс - это курс с известной позиции s к целевой позиции т с минимальными усилиями. Если не принимать во внимание влияние ветра и океанских течений, оптимальным курсом является минимальное расстояние между двумя точками на поверхности океана. Вычисление курса компаса известно как обратная задача из геодезические.
В этой статье рассматривается только абстракция минимизации расстояния между s и т путешествовать по поверхности сферы с некоторым радиусом р. В каком направлении угол п относительно Севера, должно ли судно поворачиваться, чтобы достичь целевой позиции?
Глобальная геоцентрическая система координат

Позиционный угол точки т в момент s - угол, под которым зеленый и большой пунктирные круги пересекаются в s. Направления блока тыE, тыN и ось вращения ω отмечены стрелками.
Детальная оценка оптимального направления возможна, если морская поверхность аппроксимируется поверхностью шара. Стандартное вычисление помещает корабль в геодезический широта φs и геодезический долгота λs, куда φ считается положительным, если к северу от экватора, и где λ считается положительным, если к востоку от Гринвич. В глобальной системе координат с центром в центре сферы декартовы компоненты равны

и целевая позиция

Северный полюс находится на

В минимальное расстояние d это расстояние по большому кругу, который проходит через s и т. Он рассчитывается на плоскости, содержащей центр сферы и большой круг,

куда θ угловое расстояние между двумя точками, если смотреть из центра сферы, измеренное в радианы. Косинус угла рассчитывается по формуле скалярное произведение двух векторов

Если судно направляется прямо к Северному полюсу, пройденное расстояние составит

Если корабль стартует в т и плывет прямо к Северному полюсу, пройденное расстояние

Краткий вывод
В формула косинуса из сферическая тригонометрия [1] уступает для угла п между большими кругами через s которые указывают на север с одной стороны и на т с другой стороны


В формула синуса дает

Решение этого для грех θс, т а вставка в предыдущую формулу дает выражение для тангенса позиционного угла,


Длинные производные
Поскольку краткий вывод дает угол между 0 и π который не показывает знак (к западу или востоку от севера?), желателен более явный вывод, который дает отдельно синус и косинус п такое, что использование правильная ветвь арктангенса позволяет производить угол в полном диапазоне -π≤p≤π.
Вычисление начинается с построения большого круга между s и т. Он лежит в плоскости, содержащей центр сферы, s и т и построен вращающимся s под углом θс, т вокруг оси ω. Ось перпендикулярна плоскости большого круга и вычисляется нормализованным вектором перекрестное произведение из двух позиций:

Правосторонняя наклонная система координат с центром в центре сферы задается следующими тремя осями: s, ось
![{displaystyle mathbf {s} _ {perp} = omega imes {frac {1} {R}} mathbf {s} = {frac {1} {sin heta _ {s, t}}} left ({egin {array} {c} cos varphi _ {t} cos lambda _ {t} (sin ^ {2} varphi _ {s} + cos ^ {2} varphi _ {s} sin ^ {2} lambda _ {s}) - cos лямбда _ {s} (sin varphi _ {s} cos varphi _ {s} sin varphi _ {t} + cos ^ {2} varphi _ {s} sin lambda _ {s} cos varphi _ {t} sin lambda _ {t}) cos varphi _ {t} sin lambda _ {t} (sin ^ {2} varphi _ {s} + cos ^ {2} varphi _ {s} cos ^ {2} lambda _ {s}) -sin lambda _ {s} (sin varphi _ {s} cos varphi _ {s} sin varphi _ {t} + cos ^ {2} varphi _ {s} cos lambda _ {s} cos varphi _ {t} cos лямбда _ {t}) cos varphi _ {s} [cos varphi _ {s} sin varphi _ {t} -sin varphi _ {s} cos varphi _ {t} cos (lambda _ {t} -lambda _ { s})] end {array}} ight)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cf6392e23b2822694c8b81ffe3c941fbe9c2c80)
и ось ω.Положение вдоль большого круга

Направление по компасу задается вставкой двух векторов s и s⊥ и вычисляя градиент вектора относительно θ в θ = 0.

Угол п задается разделением этого направления по двум ортогональным направлениям в плоскости, касательной к сфере в точке s. Два направления задаются частными производными от s относительно φ и в отношении λ, нормированные на единицу длины:



тыN указывает на север и тыE указывает на восток в позиции s.Позиционный угол п проекты s⊥в эти два направления,
 ,
,
где положительный знак означает, что положительные позиционные углы определены как север над востоком. Значения косинуса и синуса п вычисляются путем умножения этого уравнения с обеих сторон на два единичных вектора,
![{displaystyle cos p = mathbf {s} _ {perp} cdot mathbf {u} _ {N} = {frac {1} {sin heta _ {s, t}}} [cos varphi _ {s} sin varphi _ { t} -sin varphi _ {s} cos varphi _ {t} cos (lambda _ {t} -lambda _ {s})];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4102efe0cfecd18a48f842d8ccd48fdf33c06e18)
![{displaystyle sin p = mathbf {s} _ {perp} cdot mathbf {u} _ {E} = {frac {1} {sin heta _ {s, t}}} [cos varphi _ {t} sin (lambda _ {t} -lambda _ {s})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02cea96a297832ca577ee997e888f1a33a7fd35a)
Вместо того, чтобы вставлять запутанное выражение s⊥, оценка может использовать, что тройное произведение инвариантно относительно кругового сдвига аргументов:

Если atan2 используется для вычисления значения, можно уменьшить оба выражения путем деления на cos φти умножение на грех θс, т, потому что эти значения всегда положительны и эта операция не меняет знаков; тогда эффективно

Смотрите также
дальнейшее чтение
Рекомендации
внешняя ссылка
















![{displaystyle mathbf {s} _ {perp} = omega imes {frac {1} {R}} mathbf {s} = {frac {1} {sin heta _ {s, t}}} left ({egin {array} {c} cos varphi _ {t} cos lambda _ {t} (sin ^ {2} varphi _ {s} + cos ^ {2} varphi _ {s} sin ^ {2} lambda _ {s}) - cos лямбда _ {s} (sin varphi _ {s} cos varphi _ {s} sin varphi _ {t} + cos ^ {2} varphi _ {s} sin lambda _ {s} cos varphi _ {t} sin lambda _ {t}) cos varphi _ {t} sin lambda _ {t} (sin ^ {2} varphi _ {s} + cos ^ {2} varphi _ {s} cos ^ {2} lambda _ {s}) -sin lambda _ {s} (sin varphi _ {s} cos varphi _ {s} sin varphi _ {t} + cos ^ {2} varphi _ {s} cos lambda _ {s} cos varphi _ {t} cos лямбда _ {t}) cos varphi _ {s} [cos varphi _ {s} sin varphi _ {t} -sin varphi _ {s} cos varphi _ {t} cos (lambda _ {t} -lambda _ { s})] end {array}} ight)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2cf6392e23b2822694c8b81ffe3c941fbe9c2c80)






![{displaystyle cos p = mathbf {s} _ {perp} cdot mathbf {u} _ {N} = {frac {1} {sin heta _ {s, t}}} [cos varphi _ {s} sin varphi _ { t} -sin varphi _ {s} cos varphi _ {t} cos (lambda _ {t} -lambda _ {s})];}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4102efe0cfecd18a48f842d8ccd48fdf33c06e18)
![{displaystyle sin p = mathbf {s} _ {perp} cdot mathbf {u} _ {E} = {frac {1} {sin heta _ {s, t}}} [cos varphi _ {t} sin (lambda _ {t} -lambda _ {s})].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02cea96a297832ca577ee997e888f1a33a7fd35a)

