R-дерево - R-tree

Эта статья о структуре данных. Для типа метрического пространства см. Настоящее дерево.
R-дерево
Типдерево
Изобрел1984
ИзобретенныйАнтонин Гуттман
Сложность времени в нотация большой O
АлгоритмСреднийХудший случай
ПоискO (бревноMп)
Простой пример R-дерева для 2D прямоугольников
Визуализация R * -дерева для 3D точек с помощью ELKI (кубики - это страницы каталога)

R-деревья находятся древовидные структуры данных используется для методы пространственного доступа, т.е. для индексации многомерной информации, такой как географические координаты, прямоугольники или же полигоны. R-дерево было предложено Антонином Гуттманом в 1984 году.[1] и нашла значительное применение как в теоретическом, так и в прикладном контексте.[2] В реальной жизни R-дерево часто используется для хранения пространственных объектов, таких как местоположения ресторанов или многоугольников, из которых состоят типичные карты: улицы, здания, очертания озер, береговые линии и т. Д., А затем быстрое нахождение ответов на запросы. например, «Найти все музеи в пределах 2 км от моего текущего местоположения», «Получить все участки дороги в пределах 2 км от моего местоположения» (чтобы отобразить их в система навигации ) или «найти ближайшую заправку» (правда, без учета дорог). R-дерево также может ускорять поиск ближайшего соседа[3] для различных метрик расстояния, включая расстояние по дуге.[4]

Идея R-дерева

Ключевая идея структуры данных - сгруппировать близлежащие объекты и представить их с помощью минимальный ограничивающий прямоугольник на следующем более высоком уровне дерева; «R» в R-дереве означает прямоугольник. Поскольку все объекты лежат внутри этого ограничивающего прямоугольника, запрос, который не пересекает ограничивающий прямоугольник, также не может пересекать ни один из содержащихся в нем объектов. На уровне листа каждый прямоугольник описывает отдельный объект; на более высоких уровнях агрегация увеличивающегося числа объектов. Это также можно рассматривать как более грубую аппроксимацию набора данных.

Подобно B-дерево, R-дерево также является сбалансированным деревом поиска (так что все конечные узлы находятся на одинаковой глубине), организует данные на страницах и предназначено для хранения на диске (как используется в базы данных ). Каждая страница может содержать максимальное количество записей, часто обозначаемых как . Он также гарантирует минимальное заполнение (за исключением корневого узла), однако лучшая производительность была продемонстрирована при минимальном заполнении 30–40% от максимального количества записей (B-деревья гарантируют заполнение страницы на 50% и B * -деревья даже 66%). Причина этого - более сложная балансировка, необходимая для пространственных данных, в отличие от линейных данных, хранящихся в B-деревьях.

Как и в случае с большинством деревьев, алгоритмы поиска (например, пересечение, сдерживание, поиск ближайшего соседа ) довольно просты. Ключевой идеей является использование ограничивающих рамок, чтобы решить, искать ли внутри поддерева. Таким образом, большинство узлов в дереве никогда не читаются во время поиска. Как и B-деревья, R-деревья подходят для больших наборов данных и базы данных, где узлы могут быть выгружены в память, когда это необходимо, а все дерево не может храниться в основной памяти. Даже если данные можно уместить в памяти (или кэшировать), R-деревья в большинстве практических приложений обычно обеспечивают преимущества в производительности по сравнению с простой проверкой всех объектов, когда количество объектов превышает несколько сотен или около того. Однако для приложений в памяти существуют аналогичные альтернативы, которые могут обеспечить немного лучшую производительность или их проще реализовать на практике.

Ключевая сложность R-tree состоит в том, чтобы построить эффективное дерево, которое, с одной стороны, сбалансировано (так что листовые узлы находятся на одной высоте), с другой стороны, прямоугольники не покрывают слишком много пустого пространства и не слишком сильно перекрываются ( так что во время поиска нужно обрабатывать меньше поддеревьев). Например, первоначальная идея вставки элементов для получения эффективного дерева состоит в том, чтобы всегда вставлять в поддерево, которое требует наименьшего увеличения его ограничивающего прямоугольника. После заполнения страницы данные разделяются на два набора, каждый из которых должен занимать минимальную площадь. Большая часть исследований и улучшений для R-деревьев направлена ​​на улучшение способа построения дерева и может быть сгруппирована по двум целям: построение эффективного дерева с нуля (известная как массовая загрузка) и выполнение изменений в существующем дереве (вставка и удаление).

R-деревья не гарантируют хорошего худшая производительность, но обычно хорошо работают с реальными данными.[5] Хотя больший теоретический интерес представляет (массовая загрузка) Приоритетное R-дерево вариант R-дерева оптимален для наихудшего случая,[6] но из-за повышенной сложности пока не получил особого внимания в практических приложениях.

Когда данные организованы в R-дерево, соседи на заданном расстоянии r и k ближайших соседей (для любого Lп-Норма ) всех точек можно эффективно вычислить с помощью пространственного соединения.[7][8] Это полезно для многих алгоритмов, основанных на таких запросах, например для Фактор местного выброса. ДеЛи-Клу,[9] Кластеризация связи плотности - это кластерный анализ алгоритм, который использует структуру R-tree для подобного типа пространственного соединения для эффективного вычисления ОПТИКА кластеризация.

Варианты

Алгоритм

Макет данных

Данные в R-деревьях организованы в страницы, которые могут иметь переменное количество записей (до некоторого заранее определенного максимума и обычно выше минимального заполнения). Каждая запись в не-листовой узел хранит две части данных: способ идентификации дочерний узел, а Ограничительная рамка всех записей в этом дочернем узле. Конечные узлы хранят данные, необходимые для каждого дочернего элемента, часто точку или ограничивающую рамку, представляющую дочерний элемент, и внешний идентификатор для дочернего элемента. Для точечных данных конечными записями могут быть только сами точки. Для данных многоугольников (которые часто требуют хранения больших многоугольников) обычная настройка - хранить только MBR (минимальный ограничивающий прямоугольник) многоугольника вместе с уникальным идентификатором в дереве.

Поиск

В поиск диапазона, ввод - это прямоугольник поиска (окно запроса). Поиск очень похож на поиск в B + дерево. Поиск начинается с корневого узла дерева. Каждый внутренний узел содержит набор прямоугольников и указателей на соответствующий дочерний узел, а каждый листовой узел содержит прямоугольники пространственных объектов (указатель на некоторый пространственный объект может находиться там). Для каждого прямоугольника в узле необходимо решить, перекрывает он прямоугольник поиска или нет. Если да, необходимо также поискать соответствующий дочерний узел. Поиск выполняется таким образом рекурсивно до тех пор, пока не будут пройдены все перекрывающиеся узлы. Когда достигается листовой узел, содержащиеся в нем ограничивающие рамки (прямоугольники) проверяются относительно прямоугольника поиска, и их объекты (если они есть) помещаются в набор результатов, если они лежат в пределах прямоугольника поиска.

Для приоритетного поиска, например поиск ближайшего соседа, запрос состоит из точки или прямоугольника. Корневой узел вставляется в приоритетную очередь. Пока очередь не опустеет или не будет возвращено желаемое количество результатов, поиск продолжается, обрабатывая ближайшую запись в очереди. Узлы дерева раскрываются, и их дочерние элементы повторно вставляются. Конечные записи возвращаются при обнаружении в очереди.[10] Этот подход можно использовать с различными метриками расстояния, включая расстояние по дуге для географических данных.[4]

Вставка

Чтобы вставить объект, дерево рекурсивно просматривается от корневого узла. На каждом шаге проверяются все прямоугольники в текущем узле каталога, и кандидат выбирается с помощью эвристики, такой как выбор прямоугольника, который требует наименьшего увеличения. Затем поиск спускается на эту страницу, пока не достигнет листового узла. Если листовой узел заполнен, он должен быть разделен перед выполнением вставки. Опять же, поскольку исчерпывающий поиск слишком затратен, используется эвристика для разделения узла на два. При добавлении вновь созданного узла к предыдущему уровню этот уровень снова может переполняться, и эти переполнения могут распространяться до корневого узла; когда этот узел также переполняется, создается новый корневой узел, и дерево увеличивается в высоту.

Выбор поддерева вставки

На каждом уровне алгоритму необходимо решить, в какое поддерево вставить новый объект данных. Когда объект данных полностью содержится в единственном прямоугольнике, выбор очевиден. Когда есть несколько вариантов или прямоугольников, которые необходимо увеличить, выбор может существенно повлиять на производительность дерева.

В классическом R-дереве объекты вставляются в поддерево, которое требует наименьшего увеличения. В более продвинутых R * -дерево используется смешанная эвристика. На уровне листа он пытается минимизировать перекрытие (в случае завязок предпочтительнее минимальное увеличение, а затем минимальная площадь); на более высоких уровнях оно ведет себя аналогично R-дереву, но на связях снова предпочитает поддерево с меньшей площадью. Уменьшение перекрытия прямоугольников в R * -дереве является одним из ключевых преимуществ перед традиционным R-деревом (это также является следствием других используемых эвристик, а не только выбора поддерева).

Разделение переполненного узла

Поскольку перераспределение всех объектов узла на два узла имеет экспоненциальное количество вариантов, необходимо использовать эвристику, чтобы найти наилучшее разбиение. В классическом R-дереве Гутман предложил две такие эвристики, названные QuadraticSplit и LinearSplit. При квадратичном разбиении алгоритм ищет пару прямоугольников, которая является наихудшей комбинацией в одном узле, и помещает их в качестве исходных объектов в две новые группы. Затем он ищет запись, которая имеет наибольшее предпочтение для одной из групп (с точки зрения увеличения площади), и назначает объект этой группе до тех пор, пока не будут назначены все объекты (удовлетворяющие минимальному заполнению).

Существуют и другие стратегии расщепления, такие как Сплит Грина,[11] в R * -дерево эвристика расщепления[12] (который снова пытается минимизировать перекрытие, но также предпочитает квадратичные страницы) или алгоритм линейного разделения, предложенный Энгом и Таном[13] (который, однако, может создавать очень неправильные прямоугольники, которые менее эффективны для многих реальных запросов диапазона и окон). В дополнение к более продвинутой эвристике разделения, R * -дерево также пытается избежать разделения узла, повторно вставляя некоторые из членов узла, что аналогично тому, как B-дерево уравновешивает переполненные узлы. Было показано, что это также уменьшает перекрытие и, следовательно, повышает производительность дерева.

Наконец, X-дерево[14] может рассматриваться как вариант R * -дерева, который также может решить не разделять узел, а построить так называемый суперузел, содержащий все дополнительные записи, когда он не находит подходящего разделения (в частности, для размерные данные).

Влияние различных эвристик разделения на базу данных с почтовыми округами США

  • Квадратичное расщепление Гуттмана.[1]
    Страницы в этом дереве часто пересекаются.

  • Линейное расщепление Гуттмана.[1]
    Строение еще хуже, но строится быстрее.

  • Раскол Грина.[11] Страницы пересекаются гораздо меньше, чем со стратегией Гуттмана.

  • Линейное расщепление Анг-Тан.[13]
    Эта стратегия создает нарезанные страницы, что часто приводит к снижению производительности запросов.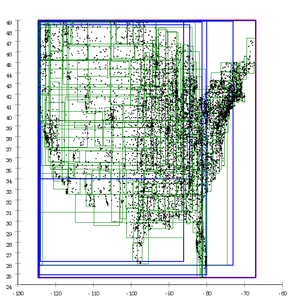

  • R * дерево топологическое расщепление.[12]
    Страницы перекрываются гораздо меньше, поскольку R * -дерево пытается минимизировать перекрытие страниц, а повторные вставки дополнительно оптимизировали дерево. Стратегия разделения предпочитает квадратные страницы, что обеспечивает лучшую производительность для обычных картографических приложений.

  • Массовая загрузка R * дерево с использованием Sort-Tile-Recursive (STR).
    Листовые страницы совсем не перекрываются, а страницы каталогов частично перекрываются. Это очень эффективное дерево, но оно требует, чтобы данные были полностью известны заранее.

  • М-деревья похожи на R-дерево, но используют вложенные сферические страницы.
    Однако разделение этих страниц намного сложнее, и страницы обычно намного больше перекрываются.

Удаление

Удаление записи со страницы может потребовать обновления ограничивающих прямоугольников родительских страниц. Однако, когда страница не заполнена, она не будет сбалансирована со своими соседями. Вместо этого страница будет растворена, и все ее дочерние элементы (которые могут быть поддеревьями, а не только конечными объектами) будут повторно вставлены. Если во время этого процесса корневой узел будет иметь единственный элемент, высота дерева может уменьшиться.

Массовая загрузка

  • Ближайший-X: объекты сортируются по их первой координате («X»), а затем разбиваются на страницы желаемого размера.
  • Упакованы R-дерево Гильберта: вариант Nearest-X, но сортировка с использованием значения Гильберта для центра прямоугольника вместо использования координаты X. Нет никакой гарантии, что страницы не будут перекрываться.
  • Сортировка-мозаика-рекурсивная (STR):[15] Другой вариант Nearest-X, который оценивает общее количество необходимых листьев как , необходимый коэффициент разделения в каждом измерении для достижения этой цели как , затем последовательно разбивает каждое измерение на разделы одинакового размера с использованием одномерной сортировки. Полученные страницы, если они занимают более одной страницы, снова загружаются массово с использованием того же алгоритма. Для точечных данных конечные узлы не будут перекрываться и «разбивать» пространство данных на страницы примерно одинакового размера.
  • Минимизация перекрытия сверху вниз (OMT):[16] Улучшение по сравнению с STR с использованием нисходящего подхода, который сводит к минимуму перекрытия между срезами и повышает производительность запросов.
  • Приоритетное R-дерево

Смотрите также

Рекомендации

  1. ^ а б c Гуттман А. (1984). "R-деревья: динамическая структура индекса для пространственного поиска" (PDF). Материалы международной конференции ACM SIGMOD 1984 по управлению данными - SIGMOD '84. п. 47. Дои:10.1145/602259.602266. ISBN  978-0897911283. S2CID  876601.
  2. ^ Ю. Манолопулос; А. Нанопулос; Я. Теодоридис (2006). R-деревья: теория и приложения. Springer. ISBN  978-1-85233-977-7. Получено 8 октября 2011.
  3. ^ Roussopoulos, N .; Kelley, S .; Винсент, Ф. Д. Р. (1995). «Запросы ближайшего соседа». Материалы международной конференции ACM SIGMOD 1995 года по управлению данными - SIGMOD '95. п. 71. Дои:10.1145/223784.223794. ISBN  0897917316.
  4. ^ а б Schubert, E .; Зимек, А .; Кригель, Х. (2013). «Геодезические дистанционные запросы на R-деревьях для индексации географических данных». Достижения в области пространственных и временных баз данных. Конспект лекций по информатике. 8098. п. 146. Дои:10.1007/978-3-642-40235-7_9. ISBN  978-3-642-40234-0.
  5. ^ Hwang, S .; Kwon, K .; Cha, S. K .; Ли, Б. С. (2003). "Оценка производительности вариантов R-дерева основной памяти". Достижения в области пространственных и временных баз данных. Конспект лекций по информатике. 2750. стр.10. Дои:10.1007/978-3-540-45072-6_2. ISBN  978-3-540-40535-1.
  6. ^ Ардж, Л.; Де Берг, М .; Haverkort, H.J .; Йи, К. (2004). «Приоритетное R-дерево» (PDF). Материалы международной конференции ACM SIGMOD 2004 по управлению данными - SIGMOD '04. п. 347. Дои:10.1145/1007568.1007608. ISBN  978-1581138597. S2CID  6817500.
  7. ^ Бринхофф, Т .; Кригель, Х.; Сигер, Б. (1993). «Эффективная обработка пространственных объединений с использованием R-деревьев». Запись ACM SIGMOD. 22 (2): 237. CiteSeerX  10.1.1.72.4514. Дои:10.1145/170036.170075.
  8. ^ Бём, Кристиан; Кребс, Флориан (01.09.2003). Поддержка приложений KDD с помощью соединения k-ближайшего соседа. Приложения баз данных и экспертных систем. Конспект лекций по информатике. Шпрингер, Берлин, Гейдельберг. С. 504–516. CiteSeerX  10.1.1.71.454. Дои:10.1007/978-3-540-45227-0_50. ISBN  9783540408062.
  9. ^ Achtert, E .; Böhm, C .; Крегер, П. (2006). DeLi-Clu: повышение надежности, полноты, удобства использования и эффективности иерархической кластеризации с помощью ранжирования ближайших пар. LNCS: достижения в области обнаружения знаний и интеллектуального анализа данных. Конспект лекций по информатике. 3918. С. 119–128. Дои:10.1007/11731139_16. ISBN  978-3-540-33206-0.
  10. ^ Kuan, J .; Льюис, П. (1997). «Быстрый поиск k ближайших соседей для семейства R-tree». Труды ICICS, 1997 Международная конференция по информации, связи и обработке сигналов. Тема: Тенденции в разработке информационных систем и беспроводной мультимедийной связи (Кат. № 97TH8237). п. 924. Дои:10.1109 / ICICS.1997.652114. ISBN  0-7803-3676-3.
  11. ^ а б Грин, Д. (1989). «Реализация и анализ производительности методов доступа к пространственным данным». [1989] Известия. Пятая международная конференция по инженерии данных. С. 606–615. Дои:10.1109 / ICDE.1989.47268. ISBN  978-0-8186-1915-1. S2CID  7957624.
  12. ^ а б Beckmann, N .; Кригель, Х.; Schneider, R .; Сигер, Б. (1990). «R * -дерево: эффективный и надежный метод доступа для точек и прямоугольников» (PDF). Материалы международной конференции ACM SIGMOD по управлению данными 1990 г. - SIGMOD '90. п. 322. CiteSeerX  10.1.1.129.3731. Дои:10.1145/93597.98741. ISBN  978-0897913652. S2CID  11567855.
  13. ^ а б Ang, C.H .; Тан, Т. С. (1997). «Новый алгоритм разделения линейных узлов для R-деревьев». В Шолле, Мишель; Voisard, Agnès (ред.). Материалы 5-го Международного симпозиума по достижениям в области пространственных баз данных (SSD '97), Берлин, Германия, 15–18 июля 1997 г.. Конспект лекций по информатике. 1262. Springer. С. 337–349. Дои:10.1007/3-540-63238-7_38.
  14. ^ Берхтольд, Стефан; Keim, Daniel A .; Кригель, Ханс-Петер (1996). «X-Tree: структура индекса для данных большого размера». Материалы 22-й конференции VLDB. Мумбаи, Индия: 28–39.
  15. ^ Leutenegger, Scott T .; Эджингтон, Джеффри М .; Лопес, Марио А. (февраль 1997 г.). "STR: простой и эффективный алгоритм упаковки R-Tree". Цитировать журнал требует | журнал = (помощь)
  16. ^ Ли, Тэвон; Ли, Сухо (июнь 2003 г.). "OMT: алгоритм минимизации перекрытия сверху вниз массовой загрузки для R-дерева" (PDF). Цитировать журнал требует | журнал = (помощь)

внешняя ссылка