Дерево (структура данных) - Tree (data structure)

В Информатика, а дерево широко используется абстрактный тип данных который моделирует иерархический древовидная структура, с корневым значением и поддеревьями потомков с родительский узел, представленный как набор связанных узлы.
Можно определить древовидную структуру данных рекурсивно как набор узлов (начиная с корневого узла), где каждый узел представляет собой структуру данных, состоящую из значения вместе со списком ссылок на узлы («потомки»), с ограничениями, что никакая ссылка не дублируется, и никто не указывает на корень.
В качестве альтернативы дерево может быть определено абстрактно как целое (глобально) как заказанное дерево, со значением, присвоенным каждому узлу. Обе эти точки зрения полезны: в то время как дерево может быть проанализировано математически в целом, когда оно фактически представлено в виде структуры данных, оно обычно представляется и обрабатывается отдельно по узлам (а не как набор узлов и список смежности ребер между узлами, так как можно представить диграф, например). Например, рассматривая дерево в целом, можно говорить о «родительском узле» данного узла, но в целом как структура данных данный узел содержит только список своих дочерних узлов, но не содержит ссылки на его родитель (если есть).
Общее использование
- Представляя иерархический такие данные как:
- Абстрактные синтаксические деревья для компьютерных языков
- Разбирать деревья для человеческих языков
- Объектные модели документов из XML и HTML документы
- JSON и YAML документы в обработке
- Деревья поиска хранить данные таким образом, чтобы алгоритм поиска возможно через обход дерева
- А двоичное дерево поиска это тип двоичное дерево
- Представляя отсортированные списки данных
- Как рабочий процесс для композитинг цифровые изображения для визуальный эффект[нужна цитата ]
- Хранение Barnes-Hut деревья, используемые для моделирования галактик
Терминология
А узел - это структура, которая может содержать значение или условие или представлять отдельную структуру данных (которая может быть собственным деревом). Каждый узел в дереве имеет ноль или более дочерние узлы, которые находятся под ним в дереве (условно деревья рисуются растущими вниз). Узел, у которого есть дочерний элемент, называется дочерним родительский узел (или же начальство ). Узел имеет не более одного родителя, но возможно много узлы-предки, например родительский родитель. Дочерние узлы с одним и тем же родителем родственные узлы.
An внутренний узел (также известный как внутренний узел, индекс для краткости, или узел ответвления) - это любой узел дерева, имеющий дочерние узлы. Точно так же внешний узел (также известный как внешний узел, листовой узел, или же конечный узел) - это любой узел, не имеющий дочерних узлов.
Самый верхний узел в дереве называется корневой узел. В зависимости от определения может потребоваться, чтобы у дерева был корневой узел (в этом случае все деревья непустые), или может быть разрешено быть пустым, и в этом случае оно не обязательно имеет корневой узел. Будучи самым верхним узлом, корневой узел не будет иметь родителя. Это узел, с которого начинаются алгоритмы в дереве, поскольку в качестве структуры данных можно переходить только от родителей к потомкам. Обратите внимание, что некоторые алгоритмы (например, поиск в глубину после упорядочения) начинаются с корня, но сначала посещают листовые узлы (получают доступ к значению листовых узлов), посещают только корень последним (т. Е. Сначала обращаются к дочерним элементам корня. , но доступ только к значению корня последним). Все остальные узлы могут быть доступны из него, следуя края или же ссылки. (В формальном определении каждый такой путь также уникален.) На диаграммах корневой узел обычно рисуется вверху. На некоторых деревьях, например кучи, корневой узел имеет особые свойства. Каждый узел в дереве можно рассматривать как корневой узел поддерева, укорененного в этом узле.
В высота узла - это длина самого длинного нисходящего пути к листу от этого узла. Высота корня - это высота дерева. В глубина узла - это длина пути к его корню (т.е. корневой путь). Это обычно необходимо при манипулировании различными самобалансирующимися деревьями, AVL деревья особенно. Корневой узел имеет нулевую глубину, листовые узлы имеют нулевую высоту, а дерево только с одним узлом (следовательно, и корнем, и листом) имеет нулевую глубину и высоту. Обычно пустое дерево (дерево без узлов, если таковые разрешены) имеет высоту -1.
А поддерево дерева Т дерево, состоящее из узла в Т и все его потомки в Т.[а][1] Таким образом, узлы соответствуют поддеревьям (каждый узел соответствует своему поддереву и всем его потомкам) - поддерево, соответствующее корневому узлу, является всем деревом, а каждый узел является корневым узлом поддерева, которое он определяет; поддерево, соответствующее любому другому узлу, называется правильное поддерево (по аналогии с правильное подмножество ).
Другие термины, используемые с деревьями:
- Сосед
- Родитель или ребенок.
- Предок
- Узел, достижимый путем повторного перехода от дочернего к родительскому.
- Потомок
- Узел, достижимый повторным переходом от родителя к потомку. Также известный как младший ребенок.
- Узел отделения
- Внутренний узел
- Узел по крайней мере с одним дочерним элементом.
- Степень
- Для данного узла его количество дочерних элементов. Лист обязательно имеет нулевую степень. Степень дерева - это степень его корня.
- Степень дерева
- Степень корня.
- Расстояние
- Количество ребер на кратчайшем пути между двумя узлами.
- Уровень
- 1 + количество ребер между узлом и корнем, т.е. (глубина + 1)[сомнительный ]
- Ширина
- Количество узлов на уровне.
- Ширина
- Количество листьев.
- лес
- Набор п ≥ 0 непересекающихся деревьев.
- Заказанное дерево
- Корневое дерево, в котором для дочерних элементов каждой вершины указан порядок.
- Размер дерева
- Количество узлов в дереве.
Предварительное определение



Дерево - это нелинейная структура данных по сравнению с массивами, связными списками, стеками и очередями, которые являются линейными структурами данных. Дерево может быть пустым без узлов или дерево представляет собой структуру, состоящую из одного узла, называемого корнем, и нуля или одного или нескольких поддеревьев.
Рисование деревьев
Деревья часто рисуют в плоскости. Упорядоченные деревья могут быть практически однозначно представлены на плоскости и поэтому называются платаны, следующим образом: если зафиксировать обычный порядок (скажем, против часовой стрелки) и расположить дочерние узлы в этом порядке (первое входящее родительское ребро, затем первое дочернее ребро и т. д.), это дает вложение дерева в плоскость, уникальное вплоть до окружающая изотопия. И наоборот, такое вложение определяет порядок дочерних узлов.
Если поместить корень наверху (родители выше детей, как в семейное древо ) и помещает все узлы, которые находятся на заданном расстоянии от корня (с точки зрения количества ребер: «уровень» дерева) на заданной горизонтальной линии, получается стандартный рисунок дерева. Для двоичного дерева первый дочерний элемент находится слева («левый узел»), а второй дочерний элемент - справа («правый узел»).
Общие операции
| График и дерево алгоритмы поиска |
|---|
| Списки |
|
| похожие темы |
- Перечисление всех предметов
- Нумерация раздела дерева
- Поиск предмета
- Добавление нового элемента в определенную позицию в дереве
- Удаление элемента
- Обрезка: Удаление целой части дерева
- Прививка: Добавление целого раздела в дерево
- Поиск корня для любого узла
- Нахождение наименьший общий предок из двух узлов
Методы обхода и поиска
Переход по элементам дерева посредством связей между родителями и детьми называется ходить по дереву, а действие - ходить дерева. Часто операция может выполняться, когда указатель достигает определенного узла. Обход, при котором каждый родительский узел проходит до его дочерних узлов, называется Предварительный заказ ходить; прогулка, при которой дети проходят путь до того, как пройдут их родители, называется почтовый заказ ходить; обход, при котором проходит левое поддерево узла, затем сам узел и, наконец, его правое поддерево, называется чтобы обход. (Этот последний сценарий, относящийся к ровно двум поддеревьям, левому поддереву и правому поддереву, предполагает, в частности, двоичное дерево.) А порядок уровней прогулка эффективно выполняет поиск в ширину по всему дереву; узлы проходят уровень за уровнем, где сначала посещается корневой узел, за ним следуют его прямые дочерние узлы и их братья и сестры, за ними следуют его внучатые узлы и их братья и сестры, и т.д., пока не будут пройдены все узлы в дереве.
Представления
Есть много разных способов представления деревьев; общие представления представляют узлы как динамически распределяется записи с указателями на их детей, их родителей или и то, и другое, или как элементы в множество, причем отношения между ними определяются их положением в массиве (например, двоичная куча ).
Действительно, двоичное дерево может быть реализовано как список списков (список, в котором значения являются списками): заголовок списка (значение первого члена) - это левый дочерний элемент (поддерево), а хвост (список второго и последующих членов) является правым потомком (поддеревом). Это также можно изменить, чтобы разрешить значения, как в Лиспе. S-выражения, где голова (значение первого члена) - это значение узла, голова хвоста (значение второго члена) - левый потомок, а хвост хвоста (список третьего и последующих членов) - правый ребенок.
Как правило, узел в дереве не имеет указателей на своих родителей, но эта информация может быть включена (расширена структура данных, чтобы также включить указатель на родительский элемент) или сохранена отдельно. В качестве альтернативы восходящие ссылки могут быть включены в данные дочернего узла, как в многопоточное двоичное дерево.
Обобщения
Диграфы
Если ребра (к дочерним узлам) рассматриваются как ссылки, тогда дерево является частным случаем орграфа, и древовидная структура данных может быть обобщена для представления ориентированные графы путем удаления ограничений, согласно которым узел может иметь не более одного родителя и что никакие циклы не допускаются. Ребра по-прежнему абстрактно рассматриваются как пары узлов, однако термины родитель и ребенок обычно заменяются другой терминологией (например, источник и цель). Разные стратегии реализации существует: орграф может быть представлен той же локальной структурой данных, что и дерево (узел со значением и список дочерних элементов), при условии, что «список дочерних элементов» является списком ссылок, или глобально такими структурами, как списки смежности.
В теория графов, а дерево это связанный ациклический график; если не указано иное, в теории графов деревья и графы считаются неориентированными. Между такими деревьями и деревьями, как структура данных, нет однозначного соответствия. Мы можем взять произвольное неориентированное дерево, произвольно выбрать одно из его вершины как корень, сделайте все его края направленными, направив их в сторону от корневого узла, создавая древообразование - и назначить порядок всем узлам. Результат соответствует древовидной структуре данных. Выбор другого корня или другой порядок приводит к другому.
Для данного узла в дереве его дочерние элементы определяют упорядоченный лес (объединение поддеревьев, заданных всеми дочерними элементами, или, что эквивалентно, взятие поддерева, данное самим узлом, и стирание корня). Подобно тому, как поддеревья естественны для рекурсии (как и при поиске в глубину), леса естественны для Corecursion (как в поиске в ширину).
Через взаимная рекурсия, лес можно определить как список деревьев (представленных корневыми узлами), где узел (дерева) состоит из значения и леса (его дочерние элементы):
f: [n [1], ..., n [k]] n: v f
Тип данных против структуры данных
Существует различие между деревом как абстрактным типом данных и конкретной структурой данных, аналогично различию между список и связанный список.
Как тип данных, дерево имеет значение и дочерние элементы, а дочерние элементы сами являются деревьями; значение и дочерние элементы дерева интерпретируются как значение корневого узла и поддеревьев дочерних элементов корневого узла. Чтобы разрешить конечные деревья, нужно либо разрешить список дочерних элементов быть пустым (в этом случае деревья могут быть непустыми, а «пустое дерево» вместо этого будет представлено лесом из нулевых деревьев), либо разрешить деревьям быть пустым, и в этом случае список дочерних элементов может иметь фиксированный размер (фактор ветвления, особенно 2 или "двоичный"), если желательно.
В качестве структуры данных связанное дерево представляет собой группу узлы, где каждый узел имеет значение и список Рекомендации другим узлам (его дочерним узлам). Также существует требование, чтобы никакие две «нисходящие» ссылки не указывали на один и тот же узел. На практике узлы в дереве обычно включают в себя и другие данные, такие как следующие / предыдущие ссылки, ссылки на их родительские узлы или почти что угодно.
За счет использования Рекомендации Что касается деревьев в структуре данных связанного дерева, деревья часто обсуждаются неявно, предполагая, что они представлены ссылками на корневой узел, поскольку часто именно так они реализуются. Например, вместо пустого дерева может быть пустая ссылка: дерево всегда непусто, но ссылка на дерево может быть пустой.
Рекурсивный
Рекурсивно, как тип данных, дерево определяется как значение (некоторого типа данных, возможно, пустое) вместе со списком деревьев (возможно, пустой список), поддеревья его дочерних элементов; символически:
- t: v [t [1], ..., t [k]]
(Дерево т состоит из стоимости v и список других деревьев.)
Более элегантно, через взаимная рекурсия, из которых дерево является одним из самых основных примеров, дерево может быть определено в терминах леса (списка деревьев), где дерево состоит из значения и леса (поддеревья его дочерних деревьев):
- f: [t [1], ..., t [k]]
- т: v f
Обратите внимание, что это определение дано в терминах ценностей и подходит для функциональные языки (предполагается ссылочная прозрачность ); разные деревья не имеют связей, поскольку представляют собой просто списки значений.
В качестве структуры данных дерево определяется как узел (корень), который сам состоит из значения (некоторого типа данных, возможно, пустого) вместе со списком ссылок на другие узлы (список, возможно, пустой, ссылки, возможно, нулевые ); символически:
- n: v [& n [1], ..., & n [k]]
(Узел п состоит из стоимости v и список ссылок на другие узлы.)
Эта структура данных определяет ориентированный граф,[b] и чтобы он был деревом, необходимо добавить условие к его глобальной структуре (его топологии), а именно, что не более одной ссылки может указывать на любой заданный узел (узел имеет не более одного родителя), и ни один узел в дереве указать на корень. Фактически, каждый узел (кроме корня) должен иметь ровно одного родителя, а корень не должен иметь родителей.
В самом деле, учитывая список узлов и для каждого узла список ссылок на его дочерние элементы, нельзя сказать, является ли эта структура деревом или нет, не проанализировав ее глобальную структуру и что на самом деле это топологически дерево, как определено ниже.
Теория типов
Как абстрактный тип данных, тип абстрактного дерева Т со значениями некоторого типа E определяется с использованием абстрактного типа леса F (список деревьев), по функциям:
- ценить: Т → E
- дети: Т → F
- ноль: () → F
- узел: E × F → Т
с аксиомами:
- значение (узел (е, ж)) = е
- дети (узел (е, ж)) = ж
С точки зрения теория типов, дерево - это индуктивный тип определяется конструкторами ноль (пустой лес) и узел (дерево с корневым узлом с заданным значением и дочерними элементами).
Математическая терминология
В целом древовидная структура данных - это заказанное дерево, обычно со значениями, прикрепленными к каждому узлу. Конкретно это (если требуется, чтобы он был непустым):
- А укоренившееся дерево с направлением «от корня» (более узкий термин - «древообразование "), смысл:
- А ориентированный граф,
- чья основная неориентированный граф это дерево (любые две вершины соединены ровно одним простым путем),
- с выделенным корнем (одна вершина обозначается как корень),
- который определяет направление на ребрах (стрелки указывают от корня; для данного ребра узел, из которого направлено ребро, называется родитель а узел, на который указывает край, называется ребенок),
вместе с:
- упорядочение дочерних узлов данного узла и
- значение (некоторого типа данных) на каждом узле.
Часто деревья имеют фиксированный (точнее, ограниченный) фактор ветвления (превосходить ), особенно всегда с двумя дочерними узлами (возможно, пустыми, следовательно в большинстве два непустой дочерние узлы), следовательно, «двоичное дерево».
Разрешение пустых деревьев делает некоторые определения более простыми, некоторые - более сложными: корневое дерево должно быть непустым, следовательно, если пустые деревья разрешены, приведенное выше определение вместо этого становится «пустым деревом или корневым деревом такое, что ...». С другой стороны, пустые деревья упрощают определение фиксированного коэффициента ветвления: с разрешенными пустыми деревьями двоичное дерево - это дерево, в котором каждый узел имеет ровно два дочерних элемента, каждый из которых является деревом (возможно, пустым). Полный набор операций с деревом должен включать операцию разветвления.
Математическое определение
Эта секция может содержать чрезмерное количество сложных деталей, которые могут заинтересовать только определенную аудиторию. (Август 2020 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Неупорядоченное дерево
Математически неупорядоченное дерево[2] (или «алгебраическое дерево»)[3] можно определить как алгебраическая структура (Икс, родитель) куда Икс непустой несущий набор узлы и родитель это функция на Икс который присваивает каждому узлу Икс его "родительский" узел, родитель (Икс). Структура подчиняется условию, что каждый непустой подалгебра должно быть то же самое фиксированная точка. То есть должен быть уникальный «корневой» узел р, так что родитель (р) = р и для каждого узла Икс, какое-то итеративное приложение родитель (родитель (⋯ родитель (Икс)⋯)) равно р.
Есть несколько эквивалентных определений.
В качестве ближайшей альтернативы можно определить неупорядоченные деревья как частичный алгебры (Икс, родитель) которые получаются из описанных выше тотальных алгебр, если родитель (р) быть неопределенным. То есть корень р единственный узел, на котором родитель функция не определена и для каждого узла Икс, корень достижимый из Икс в ориентированный граф (Икс, родитель). Это определение фактически совпадает с определением антидревесение. В TAoCP книга использует термин ориентированное дерево.[4]
| An неупорядоченное дерево это структура (Икс, ≺) куда Икс это набор узлы и ≺ это от ребенка к родителю отношение между узлами такое, что: | |
| (1) | Икс не пусто. |
|---|---|
| (2) | Икс слабо связаны в ≺. |
| (3) | ≺ является функциональный. |
| (4) | ≺ удовлетворяет АКК: не существует бесконечной последовательности Икс1 ≺ Икс2 ≺ Икс3 ≺ ⋯. |
Прямоугольник справа описывает частичную алгебру (Икс, родитель) как реляционная структура (Икс, ≺). Если (1) заменить на
- Икс содержит ровно один ≺-максимальный узел.
тогда условие (2) становится избыточным.
Используя это определение, можно предоставить специальную терминологию для обобщений неупорядоченных деревьев, которые соответствуют выделенным подмножествам перечисленных условий:
- (1,2,3) – направленное псевдодерево,
- (3) – направленный псевдолес,
- (3,4) - неупорядоченный лес (компоненты которого - неупорядоченные деревья),
- (4) – ориентированный ациклический граф, предположил, что Икс конечно,
- (1 ', 4) - ациклический доступный точечный граф (тогда условие (2) выполняется неявно).
Другое эквивалентное определение неупорядоченного дерева - это определение теоретико-множественное дерево однокорневой и высотой не более ω ("конечное" дерево).[5] То есть алгебраические структуры (Икс, родитель) эквивалентны частичные заказы (Икс, ≤) у которых есть верхний элемент р и каждый главный расстроен (он же главный фильтр ) является конечным цепь. Чтобы быть точным, следует говорить о обратный теоретико-множественное дерево, поскольку в теоретико-множественном определении обычно используется противоположный порядок.
Соответствие между (Икс, родитель) и (Икс, ≤) устанавливается через рефлексивный переходное закрытие / снижение, при этом сокращение приводит к "частичной" версии без корневого цикла.
Определение деревья в описательной теории множеств (DST) использует представление частичных заказов (Икс, ≥) в качестве префикс порядки между конечными последовательностями. Оказывается, что до изоморфизм, существует взаимно однозначное соответствие между (обратным) деревьями DST и древовидными структурами, определенными до сих пор.
Мы можем ссылаться на четыре эквивалентных характеризации как на дерево как алгебра, дерево как частичная алгебра, дерево как частичный заказ, и дерево в порядке префикса. Существует также пятое эквивалентное определение - определение корневое дерево из теории графов который представляет собой просто связанный ациклический корневой граф.
Выражение деревьев как (частичных) алгебр (также называемых функциональные графики ) (Икс, родитель) непосредственно следует за реализацией древовидных структур с использованием родительские указатели. Обычно используется частичная версия, в которой корневой узел не имеет определенного родителя. Однако в некоторых реализациях или моделях даже родитель (р) = р Установлена округлость. Известные примеры:
- Linux VFS где «У корневого дентри есть d_parent, указывающий на себя».[6].
- Концепция дерево создания[7][8][9]
из объектно-ориентированного программирования. В этом случае корневой узел - это верхний метакласс - единственный учебный класс это прямой экземпляр самого себя.
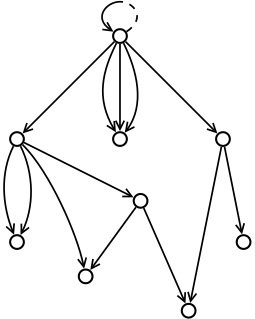
Обратите внимание, что приведенное выше определение допускает бесконечный деревья. Это позволяет описывать бесконечные структуры, поддерживаемые некоторыми реализациями через ленивая оценка. Ярким примером является бесконечный регресс из собственные классы от Рубин объектная модель.[10] В этой модели дерево, установленное через суперкласс связи между нетерминальными объектами бесконечны и имеют бесконечную ветвь (единственная бесконечная ветвь «спиральных» объектов - см. диаграмма ).
Братья и сестры
В каждом неупорядоченном дереве (Икс, родитель) есть выдающийся раздел из набора Икс узлов в братья и сестры. Два некорневых узла Икс, у принадлежат к тому же набору братьев и сестер, если родитель (Икс) = родитель (у). Корневой узел р формирует одиночка набор братьев и сестер {р}.[c] Дерево называется локально конечный или же конечно ветвление если каждый из его братьев и сестер конечен.
Каждая пара различных братьев и сестер несравненный в ≤. Вот почему слово неупорядоченный используется в определении. Такая терминология может ввести в заблуждение, когда все одноуровневые наборы являются одиночными, т.е. когда набор Икс всех узлов полностью заказанный (и поэтому хорошо организованный ) к ≤ В таком случае можно говорить о одно ветвящееся дерево вместо.
Использование включения набора
Как и в случае любого частично упорядоченного набора, древовидные структуры (Икс, ≤) может быть представлен порядок включения - к установить системы в котором ≤ совпадает с ⊆индуцированная включение порядок. Рассмотрим структуру (U, ℱ) такой, что U непустое множество, и ℱ набор подмножеств U такие, что выполняются следующие условия ( Коллекция вложенных наборов определение):
- ∅ ∉ ℱ. (То есть, (U, ℱ) это гиперграф.)
- U ∈ ℱ.
- Для каждого Икс, Y из ℱ, Икс ∩ Y ∈ {∅, Икс, Y}. (То есть, ℱ это ламинарный семья.)[11]
- Для каждого Икс из ℱ, есть только конечное количество Y из ℱ такой, что Икс ⊆ Y.
Тогда структура (ℱ, ⊆) неупорядоченное дерево, корень которого равен U. Наоборот, если (U, ≤) неупорядоченное дерево, и ℱ это набор {↓Икс | Икс ∈ U} из всех главные идеалы из (U, ≤) тогда установленная система (U, ℱ) удовлетворяет указанным выше свойствам.

Представление древовидной структуры в виде системы множеств обеспечивает семантическую модель по умолчанию - в большинстве наиболее популярных случаев древовидные структуры данных представляют иерархия сдерживания. Это также предлагает обоснование направления порядка с корнем вверху: корневой узел - это больше контейнер, чем любой другой узел. Известные примеры:
- Структура каталогов файловой системы. Каталог содержит свои подкаталоги.
- DOM-дерево. Части документа, соответствующие узлам DOM, находятся во взаимосвязи подчастей в соответствии с порядком дерева.
- Одиночное наследование в объектно-ориентированном программировании. Экземпляр класса также является экземпляром суперкласса.
- Иерархическая таксономия такой как Десятичная классификация Дьюи с участками возрастающей специфичности.
- BSP деревья, квадродеревья, Octrees, R-деревья и другие древовидные структуры данных, используемые для рекурсивных разделение пространства.
Хорошо обоснованные деревья
Неупорядоченное дерево (Икс, ≤) является обоснованный если строгий частичный порядок < это обоснованные отношения. В частности, каждое конечное дерево хорошо обосновано. Если предположить аксиома зависимого выбора дерево является хорошо обоснованным тогда и только тогда, когда у него нет бесконечной ветви.
Хорошо обоснованные деревья можно определяется рекурсивно - путем формирования деревьев из несвязного объединения меньших деревьев. Для точного определения предположим, что Икс представляет собой набор узлов. С использованием рефлексивность частичных заказов, мы можем идентифицировать любое дерево (Y, ≤) на подмножестве Икс с частичным порядком (≤) - подмножество Икс × Икс. Набор ℛ всех отношений р которые образуют хорошо обоснованное дерево (Y, р) на подмножестве Y из Икс определяется поэтапно ℛя, так что ℛ = ⋃ {ℛя | я порядковый}. Для каждого порядковый номер я, позволять р принадлежат к я-й этап ℛя если и только если р равно
- ⋃ℱ ∪ ((dom (⋃ℱ) ∪ {Икс}) × {Икс})
куда ℱ это подмножество ⋃ {ℛk | k < я} такие, что элементы ℱ попарно не пересекаются, а Икс это узел, который не принадлежит дом (⋃ℱ). (Мы используем дом (S) для обозначения домен отношения S.) Обратите внимание, что самая низкая ступень ℛ0 состоит из одноузловых деревьев {(Икс,Икс)} так как только пустой ℱ возможно. На каждом этапе (возможно) новые деревья р построены, взяв лес ⋃ℱ с компонентами ℱ с нижних ступеней и прикрепление нового корня Икс на вершине ⋃ℱ.
В отличие от дерева высота что не превосходит ω, классифицировать благоустроенных деревьев безгранично,[12] увидеть свойства "разворачиваться ".
Использование рекурсивных пар
В вычислениях общепринятым способом определения хорошо обоснованных деревьев является использование рекурсивных упорядоченных пар(F, Икс): дерево - это лес F вместе со "свежим" узлом Икс.[13] А лес F в свою очередь - возможно, пустой набор деревьев с попарно непересекающимися наборами узлов. Для точного определения действуйте так же, как при построении имена используется в теоретико-множественной технике форсинга. Позволять Икс быть набором узлов. в надстройка над Икс, определить множества Т, ℱ деревьев и лесов соответственно и карту узлы: Т → ℘(Икс) присвоение каждому дереву т базовый набор узлов, так что:
(деревья над Икс) т ∈ Т ↔ т пара (F, Икс) из ℱ × Икс такой, что для всех s ∈ F,
Икс ∉ узлы (s),(леса над Икс) F ∈ ℱ ↔ F это подмножество Т так что для каждого s,т ∈ F, s ≠ т,
узлы (s) ∩ узлы (т) = ∅ }},(узлы деревьев) у ∈ узлов (т) ↔ т = (F, Икс) ∈ Т и
либо у = Икс или же у ∈ узлов (s) для некоторых s ∈ F }}.
Окружности в приведенных выше условиях можно устранить, расслаивая каждый из Т, ℱ и узлы по этапам, как в предыдущем подразделе. Затем определите отношение "поддерево" ≤ на Т как рефлексивное транзитивное закрытие отношения "непосредственное поддерево" ≺ определяется между деревьями
s ≺ т ↔ s ∈ π1(т)
куда π1(т) это проекция из т на первую координату; т.е. это лес F такой, что т = (F, Икс) для некоторых Икс ∈ Икс. Можно заметить, что (Т, ≤) это многодерево: для каждого т ∈ Т, главный идеал ↓т заказан ≤ является хорошо обоснованным деревом как частичный порядок. Причем для каждого дерева т ∈ Т, его «узлы» - структура порядка (узлы (т), ≤т) дан кем-то Икс ≤т у если и только если есть леса F, грамм ∈ ℱ так что оба (F, Икс) и (грамм, у) являются поддеревьями т и (F, Икс) ≤ (грамм, у).
Используя стрелки
Другая формализация, а также обобщение неупорядоченных деревьев могут быть получены с помощью материализация родительско-дочерние пары узлов. Каждую такую упорядоченную пару можно рассматривать как абстрактную сущность - «стрелку». Это приводит к мультидиграф (Икс, А, s, т) куда Икс это набор узлов, А это набор стрелки, и s и т являются функциями от А к Икс присвоение каждой стрелке своего источник и цель, соответственно. На структуру распространяются следующие условия:
- (А, s ○ т–1) является неупорядоченным деревом, как тотальная алгебра.
- В т карта это биекция между стрелками и узлами.
В (1) символ композиции ○ следует интерпретировать слева направо. Условие говорит, что обратная последовательность стрелок[d] это полная карта от дочерних к родительским. Обозначим эту родительскую карту между стрелками п, т.е. п = s ○ т−1. Тогда у нас также есть s = п ○ т, таким образом, мультииграф, удовлетворяющий (1,2), также может быть аксиоматизирован как (Икс, А, п, т), с родительской картой п вместо s как определяющая составляющая. Обратите внимание, что корневая стрелка обязательно является петлей, то есть ее источник и цель совпадают.
Важное обобщение вышеупомянутой структуры достигается путем разрешения целевой карты т быть один к одному. Это означает, что (2) ослабляется до
- (2 ') т карта сюръективный - каждый узел является целью какой-либо стрелки.
Обратите внимание, что условие (1) утверждает, что только листовые стрелки могут иметь одну и ту же цель. Это ограничение из т к классифицировать из п все еще инъективный.
Мультидиграфы, удовлетворяющие (1,2 '), можно назвать «деревьями стрелок» - их характеристики дерева накладываются на стрелки, а не на узлы. Эти структуры можно рассматривать как наиболее существенную абстракцию Linux VFS, поскольку они отражают жесткую структуру файловых систем. Узлы называются inodes, стрелки Дентри (или же жесткие ссылки ). Родительская и целевая карты п и т соответственно представлены d_parent и d_inode поля в структуре данных dentry.[14] Каждому inode назначается фиксированный тип файла, из которых каталог Тип играет особую роль «задуманных родителей»:
- только inodes каталога могут отображаться как источник жесткой ссылки и
- индексный дескриптор каталога не может быть целью более чем одной жесткой ссылки.
Использование пунктирного стиля для первой половины корневого цикла означает, что, как и в случае с родительской картой, существует частичный версия для исходной карты s в котором источник корневой стрелки не определен. Этот вариант используется для дальнейшего обобщения, см. # Использование путей в мультидиграфе.
Использование путей в орграфе
Неупорядоченные деревья естественно возникают в результате «разворачивания» доступные точечные графы.[15]
Позволять ℛ = (Икс, р, р) быть заостренная реляционная структура, т.е. такие, что Икс это набор узлов, р отношение между узлами (подмножество Икс × Икс), и р является выделенным «корневым» узлом. Предположим далее, что ℛ является доступный, что обозначает Икс равно прообраз из {р} при рефлексивном переходном замыкании р, и назовем такую структуру доступный точечный граф или же пнг для краткости. (⁎) Тогда можно вывести еще один apg ℛ '= (Икс', р', р') - в разворачиваться из ℛ - следующее:
- ИКС' это набор перевернутых пути к р, т.е. множество непустых конечных последовательностей п узлов (элементы Икс) такие, что (а) последовательные члены п наоборот р-связанный, и (б) первый член п это корень р,
- Р' это отношение между путями из ИКС' такие, что пути п и q находятся Р'-связаны тогда и только тогда, когда п = q ⁎ [Икс] для какого-то узла Икс (т.е. q является максимальным собственным префикс из п, "выскочил " п), и
- р' одноэлементная последовательность [р].
Судя по всему, структура (Икс', р') является неупорядоченным деревом в версии "частичной алгебры": Р' является частичной картой, которая связывает каждый некорневой элемент Икс' к своему родителю по пути. Корневой элемент, очевидно, р'. Кроме того, выполняются следующие свойства:
- ℛ изоморфна своей развертке ℛ ' если и только если ℛ это дерево (⁑). (В частности, разворачивание идемпотент, с точностью до изоморфизма.)
- Раскладывание сохраняет обоснованность: если р хорошо обосновано, значит Р'.
- Раскладывание сохраняет ранг: Если р хорошо обоснован, то ряды р и Р' совпадают.
Примечания:
- (⁎) Чтобы установить соответствие между р и родитель карта, представленное определение использует перевернутый доступность: р доступен с любого узла. В исходном определении П. Акзель[15], каждый узел доступен из р (таким образом, вместо «прообраз» применяется слово «изображение»).[e]
- (⁑) Мы неявно ввели определение неупорядоченных деревьев как apgs: вызовите apg ℛ = (Икс, р, р) а дерево если сокращение (Икс, р) является неупорядоченным деревом как частичная алгебра. Это можно перевести как: Каждый узел доступен только по одному пути.
Использование путей в мультидиграфе
Как показано на примере жестко связанной структуры файловых систем, многие структуры данных в вычислительной технике позволяют несколько связи между узлами. Следовательно, чтобы правильно отобразить появление неупорядоченных деревьев среди структур данных, необходимо обобщить доступные точечные графы на мультидиграф параметр. Для упрощения терминологии мы используем термин колчан который является устоявшимся синонимом слова «мультидиграф».

Пусть доступный остроконечный колчан или же apq для краткости можно определить как структуру
- ℳ = (Икс, А, s, т)
куда
- Икс это набор узлы,
- А это набор стрелки,
- s это частичный функция от А к Икс (в источник карта), и
- т это полная функция от А к Икс (в цель карта).
Таким образом, ℳ это «частичный мультидиграф».
На конструкцию распространяются следующие условия:
- Есть ровно одна "корневая" стрелка, ар, чей источник s(ар) не определено.
- Каждый узел Икс ∈ Икс достижимо через конечную последовательность последовательных стрелок, начиная с корневой стрелки ар.
ℳ считается дерево если целевая карта т является взаимно однозначным соответствием стрелок и узлов. разворачиваться из ℳ формируется последовательностями, упомянутыми в (2), которые являются пути доступности (ср. Алгебра путей ). В качестве apq развертывание можно записать как
- ℳ '= (Икс', А', s', т')
куда
- ИКС' это набор путей доступности,
- А ' совпадает с ИКС',
- s ' совпадает с появлением пути, и
- т ' это личность на ИКС'.
Как и в случае с apgs, развертывание идемпотентно и всегда приводит к дереву.
В лежащий в основе пнг получается как структура
- (Икс, р, т(ар))
куда
- р = {(т(а),s(а)) | а ∈ А {ар}}.
На диаграмме выше показан пример apq со стрелками 1 + 14. В JavaScript, Python или же Рубин, структура может быть создана с помощью следующего (точно такого же) кода:
р = {}; р[1] = {}; р[2] = р[1]; р[3] = {}; р[4] = {}; р[1][5] = {}; р[1][14] = р[1][5];р[3][7] = {}; р[3][8] = р[3][7]; р[3][13] = {};р[4][9] = р[4]; р[4][10] = р[4]; р[4][11] = {};р[3][7][6] = р[3]; р[3][7][12] = р[1][5];Использование имен
Неупорядоченные деревья и их обобщения составляют суть системы именования.Существует два ярких примера систем именования: файловые системы и (вложенные) ассоциативные массивы. Представленные структуры на основе нескольких графов из предыдущих подразделов анонимный абстракции для обоих случаев. Для получения возможности именования стрелки должны быть снабжены имена в качестве идентификаторы.Имя должно быть локально уникальным - внутри каждого родственного набора стрелок.[f] может быть не более одной стрелки, помеченной данным именем.
источник | имя | цель |
|---|---|---|
| s(а) | σ(а) | т(а) |
Это можно формализовать как структуру
- ℰ = (Икс, Σ, А, s, σ, т)
куда
- Икс это набор узлы,
- Σ это набор имена,
- А это набор стрелки,
- s является частичной функцией от А к Икс,
- σ является частичной функцией от А к Σ, и
- т это полная функция от А к Икс.
Для стрелы а, составляющие тройной (s(а), σ(а), т(а)) соответственно ас источник, имя и цель. На конструкцию распространяются следующие условия:
- Редукт (Икс, А, s, т) является доступный остроконечный колчан (apq), как определено ранее.
- Функция имени σ не определено только для корневой стрелки без источника.
- Функция имени σ инъективен в ограничении на каждый родственный набор стрелок, т.е.для любых стрелок, не являющихся корневыми а, б, если s(а) = s(б) и σ(а) = σ(б) тогда а = б.
Эту структуру можно назвать вложенный словарь или же названный apq. В вычислительной технике такие структуры встречаются повсеместно. Таблица выше показывает, что стрелки можно рассматривать как «невещественные» как набор А' = {(s(а), σ (а), т(а)) | а ∈ А {ар}} троек источник-имя-цель. Это приводит к реляционной структуре (Икс, Σ, А') что можно рассматривать как реляционная база данных стол. Подчеркивание в источник и имя указывать первичный ключ.
Структуру можно перефразировать как детерминированную маркированная переходная система: Икс это набор "состояний", Σ это набор «ярлыков», А ' представляет собой набор «помеченных переходов». (Более того, корневой узел р = т(ар) является «начальным состоянием», а условие доступности означает, что каждое состояние достижимо из начального состояния.)

На схеме справа показан вложенный словарь. ℰ который имеет тот же базовый мультидиграф, что и в примере в предыдущем подразделе. Структура может быть создана с помощью кода ниже. Как и раньше, точно такой же код применяется для JavaScript, Python и Ruby.
Первый основание, ℰ0, создается путем однократного присвоения буквальный {...} к р. Эта структура, изображенная сплошными линиями, представляет собой "стрелка "(следовательно, это остовное дерево ). Буквальный, в свою очередь, кажется JSON сериализация ℰ0.
Впоследствии остальные стрелки создаются путем присвоения уже существующих узлов. Стрелки, вызывающие циклы, отображаются синим цветом.
р = {"а":{"а":5,"б":5},"c":{"а":{"ш":5},"c":{}},"d":{"ш":1.3}}р["б"] = р["а"]; р["c"]["б"] = р["c"]["а"]р["c"]["а"]["п"] = р["c"]; р["d"]["е"] = р["d"]["себя"] = р["d"]В Linux VFS функция имени σ представлен d_name поле в структуре данных dentry.[14] В ℰ0 Структура выше демонстрирует соответствие между структурами, представляемыми в формате JSON, и структурами файловых систем с жесткой связью. В обоих случаях существует фиксированный набор встроенных типов «узлов», один из которых является типом контейнера, за исключением того, что в JSON фактически есть два таких типа типы - Объект и массив. Если последний игнорируется (а также различие между отдельными примитивными типами данных), то предоставленные абстракции файловых систем и данных JSON одинаковы - оба являются деревьями стрелок, снабженными именами. σ и различие узлов-контейнеров.
Пути
Функция именования σ вложенного словаря ℰ естественно простирается от стрелок до путей стрелок. Каждая последовательность п = [а1, ..., ап] последовательных стрелок неявно присваивается путь (ср. Путь ) - последовательность σ(п) = [σ(а1), ..., σ(ап)] названий стрелок.[грамм]Локальная уникальность переносится на пути стрелок: разные одноуровневые пути имеют разные имена. В частности, пути стрелок, ведущих к корню, находятся во взаимно однозначном соответствии со своими именами путей. Это соответствие дает «символическое» представление о развертывании ℰ через путевые имена - узлы в ℰ глобально идентифицируются через дерево имен путей.
Заказанное дерево
Структуры, представленные в предыдущем подразделе, образуют лишь базовую «иерархическую» часть древовидных структур данных, которые появляются в вычислениях. В большинстве случаев существует также дополнительное «горизонтальное» упорядочение между братьями и сестрами. В деревья поиска порядок обычно устанавливается «ключом» или значением, связанным с каждым из братьев и сестер, но во многих деревьях это не так. Например, документы XML, списки в файлах JSON и многие другие структуры имеют порядок, который не зависит от значений в узлах, но сам является данными - сортировка абзацев романа по алфавиту приведет к потере информации.[сомнительный ]
Корреспондент расширение описанных ранее древовидных структур (Икс, ≤) можно определить, наделив каждый набор братьев и сестер линейным порядком следующим образом.[17][18]
Альтернативное определение по Кубояме[2] представлен в следующем подразделе.
An заказанное дерево это структура (Икс, ≤V, ≤S) куда Икс непустой набор узлов и ≤V и ≤S отношения на Икс называется vэротический (или также иерархический[2]) порядок и sиблинг порядок соответственно. На конструкцию распространяются следующие условия:
- (Икс, ≤V) - это частичный порядок, представляющий собой неупорядоченное дерево, как определено в предыдущем подразделе.
- (Икс, ≤S) это частичный заказ.
- Отчетливые узлы сопоставимы по <S тогда и только тогда, когда они братья и сестры:
- (<S) ∪ (>S) = ((≺V) ○ (≻V)) ∖ я быИкс.
- У каждого узла есть только конечное число предшествующих братьев и сестер, то есть каждый главный идеал (Икс, ≤S) конечно. (Это условие можно опустить в случае конечных деревьев.)
Условия (2) и (3) говорят, что (Икс, ≤S) представляет собой покомпонентный линейный порядок, каждый компонент является одноуровневым набором. Условие (4) утверждает, что если родственный набор S бесконечно тогда (S, ≤S) изоморфен (ℕ, ≤), обычный порядок натуральных чисел.
Учитывая это, есть три (другие) выделенные частичные приказы, которые однозначно задаются следующими предписаниями:
(<ЧАС) = (≤V) ○ (<S) ○ (≥V) (в часгоризонтальный порядок), (<L⁻) = (>V) ∪ (<ЧАС) (в "несогласованный" лв порядке очереди), (<L⁺) = (<V) ∪ (<ЧАС) (в "согласный" лв порядке очереди).
Это составляет "V-S-H-L±"система пяти частичных заказов ≤V, ≤S, ≤ЧАС, ≤L⁺, ≤L⁻ на той же площадке Икс узлов, в которых, кроме пары { ≤S, ≤ЧАС} любые два отношения однозначно определяют остальные три, см. таблица детерминированности.
Примечания об условных обозначениях:
- В состав отношений символ ○, используемый в этом подразделе, следует интерпретировать слева направо (как ).
- Символы < и ≤ выразить строгий и нестрогий версии частичного заказа.
- Символы > и ≥ выражают обратные отношения.
- В ≺ символ используется для покрывающее отношение из ≤ какой немедленный вариант частичного заказа.
Это дает шесть версий ≺, <, ≤, ≻, >, ≥ для одного отношения частичного порядка. Кроме ≺ и ≻, каждая версия однозначно определяет другие. Переход от ≺ к <требует, чтобы < быть транзитивно приводимым. Это всегда устраивает всех <V, <S и <ЧАС но может не выдержать <L⁺ или же <L⁻ если Икс бесконечно.
Частичные заказы ≤V и ≤ЧАСдополняют:
- (<V) ⊎ (>V) ⊎ (<ЧАС) ⊎ (>ЧАС) = Икс × Икс ∖ idИкс.
Как следствие, «согласованный» линейный порядок <L⁺ это линейное расширение из <V. По аналогии, <L⁻ является линейным продолжением >V.
Покрывающие отношения ≺L⁻ и ≺L⁺ соответствуют обход предварительного заказа и обход после заказа, соответственно. Если х ≺L⁻ у тогда, в зависимости от того, у есть предыдущий брат или нет, Икс node является либо «крайним правым» нестрогим потомком предыдущего брата у или, в последнем случае, Икс первый ребенок у. Пары последнего случая образуют соотношение (≺L⁻) ∖ (<ЧАС) которая является частичной картой, которая назначает каждому нелистовому узлу его Первый ребенок узел. По аналогии, (≻L⁺) ∖ (>ЧАС) назначает каждому нелистовому узлу с конечным числом детей его последний дочерний узел.
Определение с использованием горизонтального порядка
Определение Кубоямы «упорядоченных деревьев с укоренением»[2] использует горизонтальный порядок ≤ЧАС как определяющее отношение.[час] (См. Также Suppes.[19])
Используя введенные обозначения и терминологию, определение можно выразить следующим образом.
An заказанное дерево это структура (Икс, ≤V, ≤ЧАС) такие, что выполняются условия (1–5):
- (Икс, ≤V) частичный порядок, который является неупорядоченное дерево. (The vэротический порядок.)
- (Икс, ≤ЧАС) это частичный заказ. (The часгоризонтальный порядок.)
- Частичные заказы ≤V и ≤ЧАС дополняют: (<V) ⊎ (>V) ⊎ (<ЧАС) ⊎ (>ЧАС) = Икс × Икс ∖ idИкс.
- (То есть пары узлов, которые несравненный в (<V) сопоставимы в (<ЧАС) наоборот.)
- Частичные заказы ≤V и ≤ЧАС согласуются": (<ЧАС) = (≤V) ○ (<ЧАС) ○ (≥V).
- (То есть для каждого узла Икс, у такой, что Икс <ЧАС у, все потомки Икс должен предшествовать всем потомкам у.)
- У каждого узла есть только конечное число предыдущих братьев и сестер. (То есть для каждого бесконечного набор братьев и сестер S, (S, ≤ЧАС) имеет тип заказа натуральных чисел.) (Как и раньше, это условие можно опустить в случае конечных деревьев.)
Братский порядок (≤S) получается (<S) = (<ЧАС) ∩ ((≺V) ○ (≻V)), т.е. два различных узла находятся в порядке братьев и сестер тогда и только тогда, когда они расположены в горизонтальном порядке и являются братьями и сестрами.
Таблица детерминации
В следующей таблице показано определение "V-S-H-L±"система. Выражения отношения в теле таблицы равны одному из <V, <S, <ЧАС, <L⁻, или же <L⁺ по столбцу. Отсюда следует, что кроме пары { ≤S, ≤ЧАС}, упорядоченное дерево (Икс, ...) однозначно определяется любыми двумя из пяти отношений.
| <V | <S | <ЧАС | <L⁻ | <L⁺ | |
|---|---|---|---|---|---|
| ПРОТИВ | (≤V) ○ (<S) ○ (≥V) | ||||
| V, H | (<ЧАС) ∩ ((≺V)○(≻V)) | (>V) ∪ (<ЧАС) | (<V) ∪ (<ЧАС) | ||
| V, L⁻ | (<L⁻) ∩ ((≺V)○(≻V)) | (<L⁻) ∖ (>V) | |||
| V, L⁺ | (<L⁺) ∩ ((≺V)○(≻V)) | (<L⁺) ∖ (<V) | |||
| H, L⁻ | (>L⁻) ∖ (<ЧАС) | ||||
| H, L⁺ | (<L⁺) ∖ (<ЧАС) | ||||
| L⁻, L⁺ | (>L⁻) ∩ (<L⁺) | (<L⁻) ∩ (<L⁺) | |||
| S, L⁻ | Икс ≺V у ↔ у = infL⁻(Y) куда Y это изображение {Икс} под (≥S)○(≻L⁻) | ||||
| S, L⁺ | Икс ≺V у ↔ у = supL⁺(Y) куда Y это изображение {Икс} под (≤S)○(≺L⁺) | ||||
В последних двух рядах инфL⁻(Y) обозначает инфимум из Y в (Икс, ≤L⁻), и Как делаL⁺(Y) обозначает супремум из Y в (Икс, ≤L⁺). В обоих рядах (≤S) соотв. (≥S) может быть эквивалентно заменен родным братом эквивалентность (≤S)○(≥S). В частности, разделение на одноуровневые множества вместе с любым из ≤L⁻ или же ≤L⁺ также достаточно для определения упорядоченного дерева. Первый рецепт на ≺V можно читать как: родитель некорневого узла Икс равняется точной нижней грани множества всех непосредственных предшественников братьев и сестер Икс, где слова «infimum» и «предшественники» означают ≤L⁻. Точно так же и со вторым рецептом, просто используйте «супремум», «преемники» и ≤L⁺.
Отношения ≤S и ≤ЧАС очевидно, не может образовать определяющую пару. В качестве простейшего примера рассмотрим упорядоченное дерево ровно с двумя узлами - тогда нельзя сказать, какой из них является корнем.
Оси XPath
| Ось XPath | Связь |
|---|---|
предок | <V |
предок или я | ≤V |
ребенок | ≻V |
потомок | >V |
потомок или я | ≥V |
следующий | <ЧАС |
следующий брат | <S |
родитель | ≺V |
предшествующий | >ЧАС |
предыдущий брат | >S |
себя | я быИкс |
В таблице справа показано соответствие введенных отношений Оси XPath, которые используются в структурированный документ системы для доступа к узлам, которые имеют определенные отношения упорядочения к начальному «контекстному» узлу. Для узла контекста[20] Икс, это ось названный спецификатором в левом столбце набор узлов, равный изображение из {Икс} по корреспондентскому отношению. По состоянию на XPath 2.0, узлы "возвращаются" в порядок документов, который является «дискордантным» линейным порядком ≤L⁻. «Согласованность» будет достигнута, если вертикальный порядок ≤V был определен противоположным образом, с направлением снизу вверх от корня, как в теории множеств, в соответствии с естественным деревья.[я]
Карты обхода
Ниже приведен список частичные карты которые обычно используются для упорядоченного обхода дерева.[21] Каждая карта отличается функциональный подотношение ≤L⁻ или его противоположность.
- ≺V ... родительский узел частичная карта,
- ≻S ... предыдущий брат частичная карта,
- ≺S ... ближайший брат частичная карта,
- (≺L⁻) ∖ (<ЧАС) ... Первый ребенок частичная карта,
- (≻L⁺) ∖ (>ЧАС) ... последний ребенок частичная карта,
- ≻L⁻ ... предыдущий узел частичная карта,
- ≺L⁻ ... следующий узел частичная карта.
Генерирующая структура
Карты обхода составляют частичную унарная алгебра[22] (Икс, родитель, предыдущий брат, ..., следующий узел) который формирует основу для представления деревьев как связанные структуры данных. По крайней мере, концептуально существуют родительские ссылки, родственные связи смежности и первые / последние дочерние ссылки. Это также относится к неупорядоченным деревьям в целом, что можно наблюдать на Дентри структура данных в Linux VFS.[23]
Аналогично "V-S-H-L"±В системе частичных порядков есть пары карт обхода, которые однозначно определяют всю упорядоченную древовидную структуру. Естественно, одна такая порождающая структура (Икс, V, S) который можно записать как (Икс, родитель, nextSibling) - структура родительских и соседних ссылок. Еще одна важная генерирующая структура - это (Икс, firstChild, nextSibling) известный как бинарное дерево с левым потомком и правым братом. Эта частичная алгебра устанавливает взаимно однозначное соответствие между бинарные деревья и заказал деревья.
Определение с использованием бинарных деревьев
Соответствие бинарным деревьям дает краткое определение упорядоченных деревьев как частичных алгебр.
An заказанное дерево это структура куда Икс непустой набор узлов, а lc, RS частичные карты на Икс называется лeft-cребенок и рполет-sиблинг, соответственно. На конструкцию распространяются следующие условия:
- Частичные карты lc и RS не пересекаются, т.е. (lc) ∩ (RS) = ∅ .
- Обратное (lc) ∪ (RS) это частичная карта п такая, что частичная алгебра (Икс, п) - неупорядоченное дерево.
Структура частичного порядка (Икс, ≤V, ≤S) получается следующим образом:
(≺S) = (RS), (≻V) = (lc) ○ (≤S).
Кодирование последовательностями
Упорядоченные деревья можно естественным образом закодировать конечными последовательностями натуральных чисел.[24][j] Обозначим ω⁎ множество всех конечных последовательностей натуральных чисел. Тогда любое непустое подмножество W из ω⁎ это закрыто префиксы дает начало упорядоченному дереву: возьмите порядок префиксов для ≥V и лексикографический порядок за ≤L⁻. И наоборот, для упорядоченного дерева Т = (Икс, V, ≤L⁻) назначить каждый узел Икс последовательность индексов братьев и сестер, то есть корню назначается пустая последовательность, а для каждого некорневого узла Икс, позволять ш(Икс) = ш(родитель (Икс)) ⁎ [я] куда я количество предшествующих братьев и сестер Икс и ⁎ это конкатенация оператор. Положить W = {ш(Икс) | Икс ∈ Икс}. потом W, снабженный индуцированными заказами ≤V (обратный порядок префиксов) и ≤L⁻ (лексикографический порядок), изоморфен Т.
Поуровневый заказ

В качестве возможного расширения "V-S-H-L±"системы, можно определить другие особые отношения между узлами на основе дерева структура уровней. Сначала обозначим через ∼E отношение эквивалентности, определяемое Икс ∼E у если и только если Икс и у имеют одинаковое количество предков. Это приводит к разбиению множества узлов на уровни L0, L1, ... (, Lп) - а грубость раздела на братья и сестры. Затем определим отношения <E, <B⁻ и <B⁺ к
Можно заметить, что <E является строгим частичным порядком и <B⁻ и <B⁺ строгие общие заказы. Более того, есть сходство между "V-S-L"±"и" V-E-B±"системы: <E покомпонентно линейно и ортогонально <V, <B⁻ является линейным продолжением <E и из >V, и <B⁺ является линейным продолжением <E и из <V.
Смотрите также
- Древовидная структура
- Дерево (теория графов)
- Дерево (теория множеств)
- Кардинальное дерево и Порядковое дерево
- Иерархия (математика)
- Диалоговое дерево
- Одиночное наследование
- Генеративная грамматика
- Иерархическая кластеризация
- Дерево разделов двоичного пространства
- Рекурсия
- Дерево фенвик
Другие деревья
- Trie
- Алгоритм Дэй – Стаута – Уоррена
- Анфилады
- Бинарное дерево левого потомка и правого брата
- Иерархическая временная память
Примечания
- ^ Это отличается от формального определения поддерева, используемого в теории графов, которое представляет собой подграф, образующий дерево - он не обязательно должен включать всех потомков. Например, корневой узел сам по себе является поддеревом в смысле теории графов, но не в смысле структуры данных (если только нет потомков).
- ^ Собственно, корневой упорядоченный ориентированный граф.
- ^ В качестве альтернативы можно использовать «частичную» версию, исключив .
- ^ Стрелки а и б как говорят последовательныйсоответственно, если т(а) = s(б).
- ^ Однако некоторые авторы также вводят определение с обратной достижимостью.[16]
- ^ Т.е. стрелки с одним и тем же исходным узлом.
- ^ Здесь мы предполагаем, что корневая стрелка ар не в п.
- ^ К сожалению, автор использует термин родственный порядок для отношения горизонтального порядка. Это нестандартно, если не ошибочно.
- ^ Это также установило бы соответствие двух возможных направлений символов неравенства с категоризацией осей XPath в передние оси и обратные оси.
- ^ В общем, любой алфавит с упорядочением, изоморфным порядку натуральных чисел.
Рекомендации
- ^ Вайсштейн, Эрик В. «Поддерево». MathWorld.
- ^ а б c d Тетсудзи Кубояма (2007). «Сопоставление и обучение на деревьях» (PDF). Докторская диссертация, Токийский университет.
- ^ «Модель Linux VFS: структура именования».
- ^ Дональд Кнут. Искусство программирования, Том 1: Фундаментальные алгоритмы, Третье издание. Addison-Wesley, 1997. Раздел 2.3.4.2: Ориентированные деревья.
- ^ Унгер, Спенсер (2012). "Деревья в теории множеств" (PDF). Цитировать журнал требует
| журнал =(помощь) - ^ Брюс Филдс. «Примечания к ядру Linux».
- ^ Пьер Куант (1987). «Метаклассы - это первый класс: модель ObjVlisp». Материалы конференции OOPSLA '87 по системам, языкам и приложениям объектно-ориентированного программирования. Северная Голландия.
- ^ Вольфганг Клас, Михаэль Шрефль (1995). Метаклассы и их применение: адаптация модели данных и интеграция с базой данных. Springer.
- ^ "Что такое метакласс?".
- ^ «Объектная модель Ruby: подробно о структуре данных».
- ^ Б. Корте, Дж. Выген (2012). Комбинаторная оптимизация. Спрингер, Гейдельберг.
- ^ Дасгупта, Абхиит (2014). Теория множеств: с введением в реальные множества точек. Нью-Йорк: Биркхойзер.
- ^ Макинсон, Дэвид (2012). Наборы, логика и математика для вычислений. Springer Science & Business Media. ISBN 9781447124993.
- ^ а б Бове, Даниэль; Чезати, Марко (2005). Понимание ядра Linux. О'Рейли. ISBN 9780596554910.
- ^ а б Aczel, Питер (1988), Необоснованные наборы., Лекционные заметки CSLI, 14, Стэнфорд, Калифорния: Стэнфордский университет, Центр изучения языка и информации, ISBN 0-937073-22-9, МИСТЕР 0940014
- ^ А. С. Дагиги, М. Гольшани, Дж. Д. Хэмкинс и Э. Йержабек (2014). «Основополагающая аксиома и элементарные самовложения Вселенной». Бесконечность, вычислимость и метаматематика: Festschrift празднует 60-летие Петера Кёпке и Филипа Велча. arXiv:1311.0814. Bibcode:2013arXiv1311.0814S. CiteSeerX 10.1.1.764.742.CS1 maint: использует параметр авторов (связь)
- ^ Ян Хиддерс; Филипп Михильс; Роэль Веркаммен (2005). «Оптимизация сортировки и исключения дубликатов в выражениях пути XQuery» (PDF). Цитировать журнал требует
| журнал =(помощь) - ^ Фритьоф Дау; Марк Сифер (2007). «Формализм для навигации и редактирования структуры XML-документа» (PDF). Международный семинар по базам данных в сетевых информационных системах. Шпрингер, Берлин, Гейдельберг.
- ^ Суппес, Патрик (1973). «Семантика контекстно-свободных фрагментов естественных языков». Подходы к естественному языку. Спрингер, Дордрехт: 370–394. CiteSeerX 10.1.1.398.2289. Дои:10.1007/978-94-010-2506-5_21. ISBN 978-90-277-0233-3.
- ^ "XML Path Language (XPath) 3.1". Консорциум World Wide Web. 21 марта 2017.
- ^ «Обход объектной модели документа». W3C. 2000 г.
- ^ «Унарные алгебры».
- ^ J.T. Мюльберг, Г. Люттген (2009). «Проверка кода скомпилированной файловой системы». Формальные методы: основы и приложения: 12-й Бразильский симпозиум по формальным методам. Шпрингер, Берлин, Гейдельберг. CiteSeerX 10.1.1.156.7781. Цитировать журнал требует
| журнал =(помощь) - ^ Л. Афанасьев; П. Блэкберн; И. Димитриу; Б. Гайфф; Э. Горис; М. Маркс; М. де Рийке (2005). «PDL для заказанных деревьев» (PDF). Журнал прикладной неклассической логики. 15 (2): 115–135. Дои:10.3166 / jancl.15.115-135. S2CID 1979330.
дальнейшее чтение
- Дональд Кнут. Искусство программирования: Фундаментальные алгоритмы, Третье издание. Аддисон-Уэсли, 1997. ISBN 0-201-89683-4 . Раздел 2.3: Деревья, стр. 308–423.
- Томас Х. Кормен, Чарльз Э. Лейзерсон, Рональд Л. Ривест, и Клиффорд Штайн. Введение в алгоритмы, Второе издание. MIT Press и McGraw-Hill, 2001. ISBN 0-262-03293-7 . Раздел 10.4: Представление корневых деревьев, стр. 214–217. Главы 12–14 (Деревья двоичного поиска, красно-черные деревья, дополнительные структуры данных), стр. 253–320.
внешняя ссылка
- Деревья данных как средство представления комплексного анализа данных Салли Книп, 8 августа 2013 г.
- Описание от Словарь алгоритмов и структур данных
- CRAN - Пакет data.tree реализация древовидной структуры данных на языке программирования R
- WormWeb.org: интерактивная визуализация C. elegans Дерево ячеек - Визуализируйте все дерево происхождения клеток нематоды C. elegans (javascript)
- Бинарные деревья Л. Эллисон






