K-d дерево - K-d tree

k-d дерево
Тип	Многомерный BST
Изобрел	1975
Изобретенный	Джон Луи Бентли
Сложность времени в нотация большой O
Алгоритм Средний Худший случай Космос ${ Displaystyle О (п)}$ ${ Displaystyle О (п)}$ Поиск ${ Displaystyle О ( журнал п)}$ ${ Displaystyle О (п)}$ Вставить ${ Displaystyle О ( журнал п)}$ ${ Displaystyle О (п)}$ Удалить ${ Displaystyle О ( журнал п)}$ ${ Displaystyle О (п)}$

3-х мерный k-d дерево. Первое разделение (красная вертикальная плоскость) разрезает корневую ячейку (белая) на две части, каждая из которых затем разделяется (зелеными горизонтальными плоскостями) на две части. Наконец, четыре ячейки разделяются (четырьмя синими вертикальными плоскостями) на две части. Поскольку разделения больше нет, последние восемь называются листовыми ячейками.

В Информатика, а k-d дерево (Короче для k-мерный дерево ) это разделение пространства структура данных для организации точки в k-размерный Космос. k-d деревья представляют собой полезную структуру данных для нескольких приложений, таких как поиск с использованием многомерного ключа поиска (например, поиск по диапазону и поиск ближайшего соседа ). k-d деревья являются частным случаем разделение двоичного пространства деревья.

Неформальное описание

В k-d дерево - это двоичное дерево в котором каждый листовой узел - это k-мерная точка. Каждый нелистовой узел можно рассматривать как неявно генерирующий разбиение гиперплоскость который делит пространство на две части, известные как полупространства. Точки слева от этой гиперплоскости представлены левым поддеревом этого узла, а точки справа от гиперплоскости представлены правым поддеревом. Направление гиперплоскости выбирается следующим образом: каждый узел дерева связан с одним из k размеров, причем гиперплоскость перпендикулярна оси этого измерения. Так, например, если для определенного разбиения выбрана ось «x», все точки в поддереве с меньшим значением «x», чем узел, появятся в левом поддереве, а все точки с большим значением «x» будут в правом поддереве. В таком случае гиперплоскость будет задаваться значением x точки, а ее нормальный будет единицей оси x.^[1]

Операции на k-d деревья

строительство

Поскольку существует много возможных способов выбора плоскостей разделения, выровненных по осям, существует множество различных способов построения k-d деревья. Канонический метод k-d построение дерева имеет следующие ограничения:^[2]

• При перемещении вниз по дереву происходит циклическое переключение осей, используемых для выбора плоскостей разделения. (Например, в трехмерном дереве корень будет иметь Икс-выровненной плоскости, дочерние элементы корня будут иметь yвыровненные самолеты, все внуки рута будут иметь zвыровненные самолеты, у всех правнуков рута будет Икс-выровненные самолеты, праправнуки рута будут иметь yвыровненные самолеты и т. д.)
• Точки вставляются путем выбора медиана баллов, помещаемых в поддерево относительно их координат на оси, используемой для создания плоскости разделения. (Обратите внимание на предположение, что мы кормим весь набор п указывает на алгоритм заранее.)

Этот метод приводит к сбалансированный k-d дерево, в котором каждый листовой узел находится примерно на одинаковом расстоянии от корня. Однако сбалансированные деревья не обязательно оптимальны для всех приложений.

Обратите внимание, что это не требуется для выбора средней точки. В случае, если средние точки не выбраны, нет гарантии, что дерево будет сбалансировано. Чтобы избежать кодирования сложного О (п) нахождение медианы алгоритм^[3][4] или используя О (п журнал п) сортировка, например heapsort или Сортировка слиянием отсортировать все п точек, популярной практикой является сортировка фиксированный количество случайно выбранный точек и используйте медианное значение этих точек в качестве плоскости разделения. На практике этот метод часто приводит к хорошо сбалансированным деревьям.

Учитывая список п точек, следующий алгоритм использует сортировку с нахождением медианы для построения сбалансированной k-d дерево, содержащее эти точки.

функция kdtree (список точек pointList, int глубина){ // Выбираем ось по глубине, чтобы ось проходила через все допустимые значения    вар int ось: = глубина мод k; // Список точек Сортировки и выберите средние, как поворотный элемент    Выбрать медиана от ось от pointList; // Создать узел и построить поддерево    node.location: = медиана; node.leftChild: = kdtree (точки в pointList перед медиана, глубина + 1); node.rightChild: = kdtree (баллы в pointList после медиана, глубина + 1); возвращаться узел;}

Часто точки «после» медианы включают только те, которые строго больше медианы. Для точек, лежащих на медиане, можно определить функцию суперключа, которая сравнивает точки во всех измерениях.^{[non sequitur ]}. В некоторых случаях допустимо, чтобы точки, равные медиане, лежали по одну сторону от медианы, например, путем разделения точек на подмножество «меньше чем» и подмножество «больше или равно».

Пример реализации

Вышеупомянутый алгоритм реализован в Язык программирования Python как следует: от коллекции импорт именованныйот оператор импорт itemgetterот pprint импорт pformatкласс Узел(именованный("Узел", "местоположение left_child right_child")): def __repr__(себя): возвращаться pformat(кортеж(себя))def kdtree(point_list, глубина: int = 0): если не point_list: возвращаться Никто k = len(point_list[0]) # предполагается, что все точки имеют одинаковый размер # Выберите ось на основе глубины, чтобы ось проходила через все допустимые значения ось = глубина % k # Сортировка список точек по оси и выбрать средний элемент, как поворотный point_list.Сортировать(ключ=itemgetter(ось)) медиана = len(point_list) // 2 # Создать узел и построить поддеревья возвращаться Узел( расположение=point_list[медиана], left_child=kdtree(point_list[:медиана], глубина + 1), right_child=kdtree(point_list[медиана + 1 :], глубина + 1), )def главный(): "" "Пример использования" "" point_list = [(7, 2), (5, 4), (9, 6), (4, 7), (8, 1), (2, 3)] дерево = kdtree(point_list) Распечатать(дерево)если __имя__ == "__главный__": главный() Результат будет: ((7, 2), ((5, 4), ((2, 3), None, None), ((4, 7), None, None)), ((9, 6), ((8, 1), Нет, Нет), Нет)) Сгенерированное дерево показано ниже. 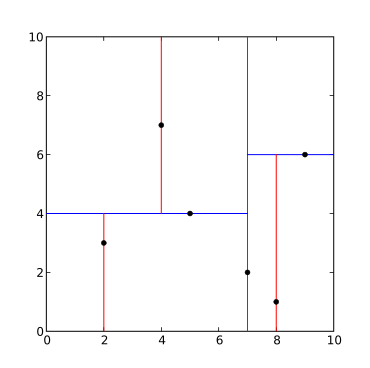k-d разложение дерева для набора точек (2,3), (5,4), (9,6), (4,7), (8,1), (7,2). Результирующий k-d дерево.

Этот алгоритм создает инвариантный что для любого узла все узлы слева поддерево находятся на одной стороне раскола самолет, а все узлы в правом поддереве находятся на другой стороне. Точки, лежащие в плоскости разделения, могут появиться с обеих сторон. Плоскость разделения узла проходит через точку, связанную с этим узлом (обозначенную в коде как node.location).

Альтернативные алгоритмы построения сбалансированного k-d дерево предварительно отсортируйте данные перед построением дерева. Затем они поддерживают порядок предварительной сортировки во время построения дерева и, следовательно, исключают дорогостоящий этап поиска медианы на каждом уровне подразделения. Два таких алгоритма создают сбалансированный k-d дерево отсортировать треугольники, чтобы сократить время выполнения трассировка лучей для трехмерного компьютерная графика. Эти алгоритмы предварительной сортировки п треугольников до построения k-d дерево, затем постройте дерево в О (п журнал п) время в лучшем случае.^[5][6] Алгоритм, строящий сбалансированный k-d дерево для сортировки точек сложность наихудшего случая равна О (кн журнал п).^[7] Этот алгоритм преобразует п очков в каждом из k размеры с использованием О (п журнал п) сортировка, например Heapsort или Сортировка слиянием перед построением дерева. Затем он поддерживает порядок этих k выполняет предварительную сортировку во время построения дерева и тем самым избегает нахождения медианы на каждом уровне подразделения.

Добавление элементов

Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Ноябрь 2008 г.)

Один добавляет новую точку к k-d дерево так же, как добавляется элемент к любому другому дерево поиска. Сначала обойдите дерево, начиная с корня и двигаясь либо к левому, либо к правому дочернему элементу, в зависимости от того, находится ли вставляемая точка «слева» или «справа» от плоскости разделения. Как только вы дойдете до узла, под которым должен располагаться дочерний элемент, добавьте новую точку как левый или правый дочерний элемент листового узла, опять же в зависимости от того, на какой стороне плоскости разделения узла находится новый узел.

Добавление точек таким образом может привести к разбалансировке дерева, что приведет к снижению производительности дерева. Скорость снижения производительности дерева зависит от пространственного распределения добавляемых точек дерева и количества добавляемых точек по отношению к размеру дерева. Если дерево становится слишком несбалансированным, может потребоваться повторная балансировка для восстановления производительности запросов, основанных на балансировке дерева, таких как поиск ближайшего соседа.

Удаление элементов

Эта секция нуждается в расширении. Вы можете помочь добавляя к этому. (Февраль 2011 г.)

Чтобы удалить точку из существующего k-d tree, не нарушая инварианта, самый простой способ - сформировать набор всех узлов и листьев из дочерних узлов целевого узла и воссоздать эту часть дерева.

Другой подход - найти замену удаленной точке.^[8] Сначала найдите узел R, содержащий точку, которую нужно удалить. Для базового случая, когда R - листовой узел, замена не требуется. В общем случае найдите точку замены, скажем p, из поддерева с корнем R. Замените точку, хранящуюся в R, на p. Затем рекурсивно удалите p.

Для поиска точки замены, если R различает x (скажем) и у R есть правильный дочерний элемент, найдите точку с минимальным значением x из поддерева, имеющего корень в правом дочернем элементе. В противном случае найдите точку с максимальным значением x из поддерева с корнем слева.

Балансировка

Балансировка k-d дерево требует ухода, потому что k-d деревья сортируются по нескольким измерениям, поэтому вращение деревьев техника не может быть использована для их баланса, так как это может нарушить инвариант.

Несколько вариантов сбалансированного k-d деревья существуют. Они включают разделенные k-d дерево, псевдо k-d дерево, K-D-B-дерево, hB-tree и Bkd-дерево. Многие из этих вариантов адаптивные k-d деревья.

Поиск ближайшего соседа

Воспроизвести медиа

Пример поиска ближайшего соседа в двумерном дереве. Здесь дерево уже построено, каждый узел соответствует прямоугольнику, каждый прямоугольник разделен на два равных подпрямоугольника, а листья соответствуют прямоугольникам, содержащим одну точку.

В поиск ближайшего соседа (NN) алгоритм направлен на поиск точки в дереве, ближайшей к заданной входной точке. Этот поиск можно выполнять эффективно, используя свойства дерева для быстрого устранения больших частей пространства поиска.

Поиск ближайшего соседа в k-d дерево действует следующим образом:

1. Начиная с корневого узла, алгоритм рекурсивно перемещается вниз по дереву, так же, как если бы точка поиска была вставлена ​​(т. Е. Идет влево или вправо в зависимости от того, больше или меньше точка, чем текущий узел в разделенное измерение).
2. Как только алгоритм достигает листового узла, он проверяет эту узловую точку, и, если расстояние лучше, эта узловая точка сохраняется как «текущая лучшая».
3. Алгоритм раскручивает рекурсию дерева, выполняя следующие шаги на каждом узле:
   1. Если текущий узел ближе, чем текущий лучший, он становится лучшим на текущий момент.
   2. Алгоритм проверяет, могут ли быть какие-либо точки с другой стороны плоскости разделения, которые находятся ближе к точке поиска, чем текущая лучшая. По идее, это делается путем пересечения разбиения гиперплоскость с гиперсфера вокруг точки поиска, радиус которой равен текущему ближайшему расстоянию. Поскольку все гиперплоскости выровнены по осям, это реализовано как простое сравнение, чтобы увидеть, меньше ли расстояние между координатой разделения точки поиска и текущим узлом, чем расстояние (общие координаты) от точки поиска до текущей наилучшей точки.
      1. Если гиперсфера пересекает плоскость, на другой стороне плоскости могут быть более близкие точки, поэтому алгоритм должен двигаться вниз по другой ветви дерева от текущего узла в поисках более близких точек, следуя тому же рекурсивному процессу, что и весь поиск .
      2. Если гиперсфера не пересекает плоскость разделения, алгоритм продолжает движение вверх по дереву, и вся ветвь на другой стороне этого узла удаляется.
4. Когда алгоритм завершает этот процесс для корневого узла, поиск завершается.

Обычно алгоритм использует квадраты расстояний для сравнения, чтобы избежать вычисления квадратных корней. Кроме того, он может сэкономить вычисления, сохраняя квадрат текущего лучшего расстояния в переменной для сравнения.

С помощью простых модификаций алгоритм может быть расширен несколькими способами. Он может обеспечить k ближайших соседей к точке, поддерживая k текущие рекорды вместо одного. Ветка удаляется только тогда, когда k точки были найдены, и ветвь не может иметь точек ближе, чем любая из k текущие рекорды.

Его также можно преобразовать в алгоритм приближения, чтобы он работал быстрее. Например, приблизительный поиск ближайшего соседа может быть достигнут путем простой установки верхней границы количества точек для исследования в дереве или прерывания процесса поиска на основе часов реального времени (что может быть более подходящим в аппаратных реализациях). Ближайший сосед для точек, которые уже находятся в дереве, может быть достигнут, не обновляя уточнение для узлов, которые дают нулевое расстояние в результате, это имеет обратную сторону отбрасывания точек, которые не уникальны, но совмещены с исходной точкой поиска .

Примерный ближайший сосед полезен в приложениях реального времени, таких как робототехника, из-за значительного увеличения скорости, достигаемого за счет отсутствия исчерпывающего поиска лучшей точки. Одна из его реализаций - поиск по наилучшему бункеру.

Поиск диапазона

Поиск диапазона ищет диапазоны параметров. Например, если дерево хранит значения, соответствующие доходу и возрасту, то поиск по диапазону может быть чем-то вроде поиска всех членов дерева, которые имеют возраст от 20 до 50 лет и доход от 50 000 до 80 000. Поскольку k-d деревья делят диапазон домена пополам на каждом уровне дерева, они полезны для выполнения поиска по диапазону.

Анализ деревьев двоичного поиска показал, что время наихудшего случая для поиска по диапазону в k-размерный k-d дерево, содержащее п узлов определяется следующим уравнением.^[9]

${ displaystyle t _ { text {худший}} = O (k cdot n ^ {1 - { frac {1} {k}}})}$

Снижение производительности при работе с данными большого размера

Найти ближайшую точку - это О (журнал п) в среднем, в случае случайно распределенных точек, хотя анализ в целом сложен.^[10]

В многомерных пространствах проклятие размерности заставляет алгоритм посещать гораздо больше ветвей, чем в пространствах с меньшей размерностью. В частности, когда количество точек лишь немного превышает количество измерений, алгоритм лишь немного лучше, чем линейный поиск всех точек. Как правило, если размерность ${ displaystyle k}$, количество точек в данных, ${ displaystyle n}$, должно быть ${ Displaystyle п gg 2 ^ {k}}$. В противном случае, когда ${ displaystyle k}$-d деревья используются с данными большой размерности, большинство точек в дереве будет оценено, а эффективность не лучше, чем полный перебор,^[11] и, если требуется достаточно хороший и быстрый ответ, вместо этого следует использовать приближенные методы ближайшего соседа.

Снижение производительности, когда точка запроса находится далеко от точек в дереве k-d

Кроме того, даже в низкоразмерном пространстве, если среднее попарное расстояние между k ближайшие соседи точки запроса значительно меньше среднего расстояния между точкой запроса и каждым из k ближайших соседей, производительность поиска ближайшего соседа ухудшается в сторону линейной, так как расстояния от точки запроса до каждого ближайшего соседа имеют одинаковую величину. (В худшем случае рассмотрим облако точек, распределенных на поверхности сферы с центром в начале координат. Каждая точка равноудалена от начала координат, поэтому поиск ближайшего соседа из начала координат должен проходить по всем точкам на поверхность сферы для идентификации ближайшего соседа, который в данном случае даже не уникален.)

Чтобы смягчить потенциально значительное снижение производительности поиска по дереву kd в худшем случае, алгоритм поиска по дереву может предоставить параметр максимального расстояния, а рекурсивный поиск может быть сокращен всякий раз, когда ближайшая точка в данной ветви дерева не может быть ближе, чем это максимальное расстояние. Это может привести к тому, что поиск ближайшего соседа не сможет вернуть ближайшего соседа, что означает, что никакие точки не находятся на этом максимальном расстоянии от точки запроса.

Сложность

• Создание статического k-d дерево из п points имеет следующую сложность наихудшего случая:
  • О (п журнал² п) если О (п журнал п) сортировка, например Heapsort или Сортировка слиянием используется для нахождения медианы на каждом уровне зарождающегося дерева;
  • О (п журнал п) если О (п) медиана медиан алгоритм^[3][4] используется для выбора медианы на каждом уровне зарождающегося дерева;
  • О (кн журнал п) если п очки предварительно отсортированы в каждом из k размеры с использованием О (п журнал п) сортировка, например Heapsort или Сортировка слиянием до строительства k-d дерево.^[7]
• Вставка новой точки в сбалансированный k-d дерево берет О (журнал п) время.
• Удаление точки из сбалансированного k-d дерево берет О (журнал п) время.
• Запрос диапазона параллельности осям в сбалансированном k-d дерево берет О (п^{1−1 / к} +м) время, где м - количество сообщенных точек, а k размер k-d дерево.
• Нахождение 1 ближайшего соседа в сбалансированном k-d дерево со случайно распределенными точками принимает О (журнал п) время в среднем.

Вариации

Объёмные объекты

Вместо очков k-d дерево также может содержать прямоугольники или гипер прямоугольники.^[12][13] Таким образом, поиск по диапазону превращается в проблему возврата всех прямоугольников, пересекающих прямоугольник поиска. Дерево строится обычным образом со всеми прямоугольниками у листьев. В поиск ортогонального диапазона, то напротив координата используется при сравнении с медианой. Например, если текущий уровень разделен по x_высоко, мы проверяем x_низкий координата прямоугольника поиска. Если медиана меньше x_низкий координата прямоугольника поиска, тогда ни один прямоугольник в левой ветви не может пересекаться с прямоугольником поиска и поэтому может быть обрезан. В противном случае необходимо пройти обе ветви. Смотрите также дерево интервалов, который является одномерным частным случаем.

Очки только в листьях

Также возможно определить k-d дерево с точками, хранящимися исключительно в листьях.^[2] Эта форма k-d tree позволяет использовать различные механики разделения, отличные от стандартного среднего разделения. Правило разделения средней точки^[14] выбирает середину самой длинной оси искомого пространства независимо от распределения точек. Это гарантирует, что соотношение сторон будет не более 2: 1, но глубина зависит от распределения точек. Вариант, называемый скользящей средней точкой, разделяется только по середине, если есть точки по обе стороны от разделения. В противном случае он разделится на точку, ближайшую к середине. Maneewongvatana и Mount показывают, что это обеспечивает "достаточно хорошую" производительность на общих наборах данных.

Используя скользящую среднюю точку, приблизительный ближайший сосед на запрос можно ответить в ${ displaystyle O left ({ tfrac {1} {{ epsilon } ^ {d}}} log n right)}$.Приблизительный подсчет дальности можно найти в ${ displaystyle O left ( log n + { left ({ tfrac {1} { epsilon }} right)} ^ {d} right)}$ этим методом.

Смотрите также

Близкие варианты:

• скрытый k-d дерево, а k-d дерево, определенное неявной функцией разделения, а не явно сохраненным набором разделений
• мин Макс k-d дерево, а k-d дерево, которое связывает минимальное и максимальное значение с каждым из его узлов
• Расслабленный k-d дерево, а k-d дерево, что дискриминанты в каждом узле произвольны

Связанные варианты:

• Quadtree, структура разделения пространства, которая одновременно разделяется на два измерения, так что каждый узел имеет 4 дочерних элемента.
• Octree, структура разделения пространства, которая одновременно разделяется в трех измерениях, так что каждый узел имеет 8 дочерних элементов.
• Шаровое дерево, многомерное разбиение пространства, полезное для поиска ближайшего соседа
• R-дерево и иерархия ограничивающих интервалов, структура для разделения объектов, а не точек, с перекрывающимися областями
• Дерево точек обзора, вариант k-d дерево, которое использует гиперсферы вместо гиперплоскостей для разделения данных

Проблемы, которые можно решить с помощью k-d деревья:

• Рекурсивное разбиение, метод построения деревьев статистических решений, подобных k-d деревья
• Клее проблема меры, задача вычисления площади объединения прямоугольников, решаемая с помощью k-d деревья
• Проблема гильотины, проблема поиска k-d дерево, ячейки которого достаточно велики, чтобы содержать заданный набор прямоугольников

Реализации с открытым исходным кодом

• АЛГЛИБ имеет реализации C # и C ++ алгоритмов ближайшего соседа на основе дерева k-d и алгоритмов приблизительного ближайшего соседа
• SciPy, библиотека Python для научных вычислений, содержит реализации алгоритмов поиска ближайшего соседа на основе дерева k-d.
• scikit-learn, библиотека Python для машинного обучения, содержит реализации k-d деревьев для поиска ближайших соседей и соседей по радиусу.

использованная литература