Надежная регрессия и обнаружение выбросов - Robust Regression and Outlier Detection
Надежная регрессия и обнаружение выбросов это книга о надежная статистика, уделяя особое внимание точка разрушения методов для надежная регрессия. Это было написано Питер Руссеув и Анник М. Лерой, опубликованная в 1987 г. Wiley.
Фон
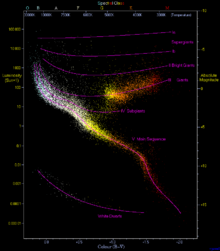
Линейная регрессия проблема вывода линейной функциональной связи между зависимая переменная и один или несколько независимые переменные, из наборов данных, где эта связь была скрыта шумом. Обычный метод наименьших квадратов предполагает, что все данные лежат около подходящей линии или плоскости, но отклоняются от нее путем добавления нормально распределенный остаточная стоимость. Напротив, надежные методы регрессии работают, даже если некоторые точки данных выбросы которые не имеют отношения к подходящей линии или плоскости, возможно, потому, что данные получены из смеси источников, или, возможно, потому, что злоумышленник пытается повредить данные, чтобы метод регрессии дал неточный результат.[1] Типичное приложение, обсуждаемое в книге, включает Диаграмма Герцшпрунга – Рассела звездных типов, в которых нужно провести кривую через главная последовательность звезд без припадка, отброшенного отдаленными гигантские звезды и белые карлики.[2] В точка разрушения надежного метода регрессии - это доля внешних данных, которую он может выдержать, оставаясь точным. Для этого стиля анализа лучше использовать более высокие точки разбивки.[1] Точка разбивки для обычных наименьших квадратов близка к нулю (один выброс может привести к тому, что подгонка станет сколь угодно далекой от оставшихся неповрежденных данных)[2] в то время как некоторые другие методы имеют точки отказа до 50%.[1] Хотя эти методы требуют немногочисленных предположений о данных и хорошо работают для данных, шум которых не совсем понятен, они могут иметь несколько меньшую эффективность, чем обычные методы наименьших квадратов (требующие большего количества данных для заданной точности подгонки), и их реализация может быть сложной и сложной. медленный.[3]
Темы
В книге семь глав.[1][4] Первый вводный; это описывает простая линейная регрессия (в котором есть только одна независимая переменная), обсуждает возможность выбросов, которые повреждают зависимую или независимую переменную, приводит примеры, в которых выбросы приводят к неверным результатам, определяет точку разбивки и кратко вводит несколько методов для надежной простой регрессии, включая повторная медианная регрессия.[1][2] Во второй и третьей главах более подробно анализируется метод наименьшей медианы квадратов для регрессии (в котором ищут соответствие, которое минимизирует медиана квадрата остатки ) и наименее обрезанные квадраты метод (в котором стараются минимизировать сумму квадратов остатков ниже медианы). Оба этих метода имеют точку разрыва 50% и могут применяться как для простой регрессии (глава 2), так и для многомерной регрессии (глава 3).[1][5] Хотя наименьшая медиана имеет привлекательное геометрическое описание (например, нахождение полосы минимальной высоты, содержащей половину данных), ее низкая эффективность приводит к рекомендации использовать вместо нее наименее обрезанные квадраты; наименее обрезанные квадраты также можно интерпретировать как использование метода наименьшей медианы для поиска и исключения выбросов, а затем использование простой регрессии для оставшихся данных,[4] и приближается к простой регрессии в своей эффективности.[6] Помимо описания этих методов и анализа их статистических свойств, эти главы также описывают, как использовать программное обеспечение авторов для реализации этих методов.[1] Третья глава также включает описание некоторых альтернативных оценок с высокими точками разбивки.[7]
В четвертой главе описана одномерная оценка параметр местоположения или же основная тенденция и его программную реализацию, а пятая глава более подробно описывает алгоритмы используется программным обеспечением для эффективного вычисления этих оценок. Шестая глава касается обнаружение выбросов, сравнение методов определения точек данных как выбросов, основанных на надежной статистике, с другими широко используемыми методами, а последняя глава посвящена проблемам определения местоположения более высокой размерности, а также Временные ряды анализ и проблемы подбора эллипсоида или ковариационная матрица к данным.[1][4][5][7] Помимо использования точки разбивки для сравнения статистических методов, в книге также рассматриваются их эквивалентность: для каких семейств преобразований данных соответствие преобразованных данных равно преобразованной версии соответствия исходным данным?[6]
В соответствии с фокусом книги на приложениях, в ней представлено множество примеров анализа, выполненного с использованием надежных методов, где полученные оценки сравниваются с оценками, полученными стандартными ненадежными методами.[3][7] Теоретический материал включен, но отложен, чтобы его могли легко пропустить читатели, менее склонные к теории. Авторы придерживаются позиции, что робастные методы могут использоваться как для проверки применимости обычной регрессии (когда результаты обоих методов совпадают), так и для замены их в случаях, когда результаты не совпадают.[5]
Аудитория и прием
Книга предназначена для прикладных статистиков с целью убедить их использовать надежные методы, которые она описывает.[1] В отличие от предыдущей работы в области надежной статистики, он делает надежные методы понятными и (через соответствующее программное обеспечение) доступными для практиков.[3] Никаких предварительных знаний надежной статистики не требуется,[4] хотя предполагается некоторый опыт в основных статистических методах.[5] Книгу также можно использовать как учебник,[5] хотя рецензент П. Дж. Лэйкок называет возможность такого использования «смелым и прогрессивным».[4] рецензенты Сехулт и Грин отмечают, что такой курс вряд ли впишется в британские учебные программы по статистике.[6]
Рецензенты Сеулт и Грин жалуются, что слишком большая часть книги действует как руководство пользователя к программному обеспечению авторов и должна была быть урезана.[6]Однако рецензент Грегори Ф. Пипель пишет, что «презентация очень хорошая», и рекомендует книгу любому пользователю статистических методов.[1] И, предлагая изменить порядок некоторых материалов, Карен Кафадар настоятельно рекомендует книгу как учебное пособие для аспирантов и справочник для профессионалов.[5] Рецензент А.С.Аткинсон кратко резюмирует книгу как «интересную и важную».[8]
Связанные книги
Было несколько предыдущих книг по надежной регрессии и обнаружению выбросов, в том числе:[5][7]
- Выявление выбросов Д. М. Хокинс (1980)
- Надежная статистика к Питер Дж. Хубер (1981)
- Введение в робастные и квазиустойчивые статистические методы У. Дж. Дж. Рей (1983)
- Понимание надежного и исследовательского анализа данных Дэвид К. Хоглин, Фредерик Мостеллер, и Джон Тьюки (1983)
- Надежная статистика Хэмпель, Рончетти, Руссеу и Стахел (1986)
В сравнении, Надежная регрессия и обнаружение выбросов сочетает в себе надежность и обнаружение выбросов.[5] Он менее теоретический, больше ориентирован на данные и программное обеспечение и больше ориентирован на точку отказа, чем на другие меры устойчивости.[7] Кроме того, он первым подчеркивает важность «рычага» - явления, когда выборки с выпадающими значениями независимой переменной могут иметь более сильное влияние на соответствие, чем выборки, в которых независимая переменная имеет центральное значение.[8]
Рекомендации
- ^ а б c d е ж грамм час я j Пипель, Грегори Ф. (май 1989 г.), "Обзор Надежная регрессия и обнаружение выбросов", Технометрика, 31 (2): 260–261, Дои:10.2307/1268828, JSTOR 1268828
- ^ а б c Зоннбергер, Гарольд (июль – сентябрь 1989 г.), "Обзор Надежная регрессия и обнаружение выбросов", Журнал прикладной эконометрики, 4 (3): 309–311, JSTOR 2096530
- ^ а б c Вайсберг, Стэнфорд (июль – август 1989 г.), "Обзор Надежная регрессия и обнаружение выбросов", Американский ученый, 77 (4): 402–403, JSTOR 27855903
- ^ а б c d е Лэйкок, П. Дж. (1989), "Обзор Надежная регрессия и обнаружение выбросов", Журнал Королевского статистического общества, серия D (Статистик), 38 (2): 138, Дои:10.2307/2348319, JSTOR 2348319
- ^ а б c d е ж грамм час Кафадар, Карен (Июнь 1989 г.), "Обзор Надежная регрессия и обнаружение выбросов", Журнал Американской статистической ассоциации, 84 (406): 617–618, Дои:10.2307/2289958, JSTOR 2289958
- ^ а б c d Seheult, A.H .; Грин, П. Дж. (1989), "Обзор Надежная регрессия и обнаружение выбросов", Журнал Королевского статистического общества, серия A (Статистика в обществе), 152 (1): 133–134, Дои:10.2307/2982847, JSTOR 2982847
- ^ а б c d е Йохай, В. Дж. (1989), "Обзор Надежная регрессия и обнаружение выбросов", Математические обзоры и zbMATH, МИСТЕР 0914792, Zbl 0711.62030
- ^ а б Аткинсон, А.С. (июнь 1988 г.), "Обзор Надежная статистика и Надежная регрессия и обнаружение выбросов", Биометрия, 44 (2): 626–627, Дои:10.2307/2531877, JSTOR 2531877
