Научные индексы и влияние - Scholar Indices and Impact
Эта статья может требовать уборка встретиться с Википедией стандарты качества. Конкретная проблема: Статью нужно сделать WP: MOS-соответствует; содержит неточности (библиометрические данные больше, чем научные указатели и т. д.), утверждения без источников и т. д. (Апрель 2012 г.) (Узнайте, как и когда удалить этот шаблон сообщения) |
Научные индексы используются для измерения вклада ученых в области их исследований. Начиная с статьи 2005 г. Хорхе Э. Хирш,[1] увеличилось использование научных индексов.
Определение
Иногда называется библиометрия индексы для ученых - это математические и статистические инструменты, которые измеряют значимость вклада, внесенного академиком в область своих исследований. Научные индексы могут включать в себя другие оценки, такие как отслеживание цитирования и рейтинг журналов.
Творчество
Любой агрегатор цитаты и ссылки, при наличии времени, денег и склонности могли бы составить собственный набор научных указателей. Издатели, известные в этой области, включают Эльзевир и Thomson Reuters.
Коммерческое программное обеспечение которые используют парсеры и Интернет поисковые системы для создания наборов научных указателей или индивидуальных результатов теперь доступны. Примеры: Опубликовать или погибнуть;[2] 'ScholarIndex ';[3] 'Scopus '[4] и 'Google ученый '.[5]
Каждый поставщик программного обеспечения в первую очередь использует свои собственные данные, а также журналы, публикации, авторитетные файлы, индексы и предметные категории для создания наборов научных указателей.
В то время как некоторые компании предоставляют данные и оцененные метрики в виде бесплатных загрузок, другие требуют подписки для покрытия затрат на производство и содержание эффективного анализатора, поисковой системы и базы данных документов.
Использовать
Научные индексы позволяют выбирать коллекции журналов, использовать исследовательские фонды, ранжировать журналы и определять значимых участников в предметной области.[6][7]
Сторонники научных индексов рекомендуют их использовать в таких областях, как службы связи, ссылки, инструкции и управление коллекциями.[8]
Критики использования индексов ученых ссылаются на их ограничения, связанные с вопросами точности, достоверности и применимости, и обсуждают их применение при найме, сроках пребывания в должности, финансировании, присуждении премий и решениях о членстве.
Хотя научные индексы могут не полностью описывать влияние работы отдельного исследователя, некоторые ученые сами определяют свои научные индексы, чтобы включать их, например, в рекламные материалы и биографические данные. Другие могут изучать свои научные индексы просто ради них самих.
Те, кто интересуется научными индексами, могут найти результаты, например проекты визуализации данных, захватывающими.
Типы
К настоящему времени разработан ряд научных указателей. Один из них - «индекс Хирша», введенный Хорхе Э. Хирш в августе 2005 г. Хирш охарактеризовал индекс Хирша как беспристрастный, поскольку он включает взаимосвязь между объемом опубликованных научных работ и количеством цитирований этих статей, что создает меньшую систематическую ошибку, чем любой из этих показателей.
Другой научный индекс - это «g-индекс», который измеряет количество цитирований всех хорошо цитируемых работ за определенный период времени. «М-фактор» был разработан, чтобы ввести ограничение по времени для индекса Хирша, который в противном случае был постоянно увеличивающейся величиной.
Другие варианты h-индекса, такие как hI-index, e-index [9] и другие разрабатываются и пересматриваются.
В Число Эрдеша [10] был разработан для измерения цепочки публикаций, начатой Полом Эрдёшем.
Все такие научные индексы количественно оценивают вклад исследователя только на основе цитирования их работ. В идеале оценка вклада исследователя в свою область должна включать как научные индексы, так и анализ качества самой работы.
индекс Хирша
В индекс Хирша индекс был предложен Хорхе Э. Хирш, а физик в UCSD, в 2005 году.[1]
Генри Шефер из Университет Джорджии США, вместе с коллегой Эми Петерсон, создали рейтинги в соответствии с индексом Хирша от ISI Web of Science. Хотя веб-приложения могут вычислять h-индексы, Петерсону приходилось проверять орфографические ошибки или повторяющиеся имена.
Индекс Хирша определяется следующим образом:
- Ученый имеет индекс час если час его или ее N документы имеют по крайней мере час цитаты то и другое (N-час) бумаги имеют не более час цитаты каждый.
Для расчета индекса Хирша статьи, написанные академиком, располагаются в порядке убывания количества цитирований. В h-индексе количество статей равно количеству цитирований (начиная с статьи с наибольшим количеством цитирований).
Хотя индекс Хирша широко используется, он не учитывает качество документов; другие статьи, цитирующие научные публикации; количество соавторов и место автора в списке авторов. Кроме того, все поля имеют одинаковое значение.
Еще одно ограничение заключается в том, что индекс Хирша не меняется со временем.[нужна цитата ]. Например, Эварист Галуа имел индекс Хирша 2, в то время как Клод Шеннон имел индекс Хирша 7,[11] увеличился до 62 в 2020 году.[12]
m-фактор
В то время как индекс Хирша не зависит от даты академической карьеры, m-фактор направлен на оценку периода академической деятельности, чтобы даже молодые ученые достигли того значения, которого они заслуживают.
Таким образом, если п= количество лет с момента первой опубликованной работы ученого, m-фактор = h-index /п.
Однако m-фактор может стабилизироваться только на более позднем этапе карьеры ученого. для исследователей на начальном этапе своей карьеры с низкими индексами h небольшие изменения h-индекса могут привести к большим изменениям m-фактора. Хирш предполагает, что первая опубликованная статья исследователя не всегда может быть подходящей отправной точкой, особенно если это был незначительный вклад, опубликованный задолго до академического периода устойчивой продуктивности.
Хотя m-фактор добавляет время в качестве весового коэффициента, он не учитывает основные недостатки h-индекса, включая качество публикации и качество цитирования.
g-индекс
g-индекс это вариант индекс Хирша, который учитывает эволюцию цитируемости наиболее цитируемых статей с течением времени.
- В комплекте бумаг есть g-индекс г, если грамм является наивысшим рангом такой, что верхние g статей вместе имеют не менее грамм^ 2 цитаты.
Другими словами, g-индекс g - самый высокий ранг (где статьи расположены в порядке убывания количества полученных ими цитирований), так что первая грамм документы имеют (вместе) не менее грамм^ 2 цитаты.
Можно доказать, что для любого набора статей g-индекс всегда существует и уникален.[13]
где Лоткаян экспонента и где Т обозначает общее количество источников.
С ,
Например, если 2 ученых имеют индекс Хирша 4, может случиться так, что один из них опубликовал 4 статьи, которые имеют 4 или более цитирования, в то время как другой ученый может опубликовать 10 статей, из которых 3 имеют более 100 цитирований, а 4-е. статья имеет 4 цитирования, а остальные - менее 4 цитирований.
В попытке предложить более высокий вес второму ученому, который в совокупности получил более 304 ссылок на 10 статей, g-индекс было предложено. Таким образом, в нашем примере первый ученый g-индекс = 4, а у второго ученого g-индекс значительно выше.
Число Эрдеша
Число Эрдеша измеряет совместное расстояние между человеком и математиком Полом Эрдешом, измеряемое авторством математических статей.
Принимая во внимание, что Пол Эрдёш имеет индекс = 0, люди, которые были соавторами с ним, имеют индекс = 1, соавторы этих соавторов имеют индекс = 2 и так далее. Таким образом, чтобы вычислить свое число Эрдёша, прибавьте 1 к числу Эрдёша любого соавтора с наименьшим числом Эрдёша. Проект Erdős-Number на Оклендский университет поддерживает веб-сайт, отслеживающий количество ученых Эрдеша по всему миру.
Одно предостережение заключается в том, что большинство зарегистрированных до сих пор чисел Эрдеша составляют 13, но среднее значение меньше 5, и почти каждый с конечным числом Эрдеша имеет число меньше 8.
Индексы Hubs и Authority
Оценка полного вклада ученого в область своих исследований может быть оценена двояко. Один из них - это количество цитирований, полученных ученым. Другой заключается в учете качества ссылок, на которые ссылается ученый.
В то время как сильная цитируемость делает ученого сильным авторитетом в своей области, наличие сильных ссылок делает ученого сильным центром, который знает всю значительную работу в этой области. Расчет индексов хаба и авторитета требует знания взаимоотношений между цитируемыми или упоминаемыми учеными.
Для вычисления этих индексов можно использовать алгоритм Hubs and Authorities. Алгоритм выполняет анализ ссылок в данной сети и присваивает два балла каждому узлу: концентратору и органу власти.[14][15]
На ценный и информативный узел в сети обычно указывает большое количество ссылок, то есть он имеет большую степень (см. Рис. 1). Такой узел называется авторитетом.[16]
Узел, указывающий на множество авторитетных узлов, сам по себе является полезным ресурсом и называется концентратором. Хаб обычно имеет большую исходящую степень. В контексте цитирования литературы хаб - это обзорная статья, в которой цитируется множество оригинальных статей, а авторитетная - это оригинальная основополагающая статья, на которую ссылаются многие статьи.[17]
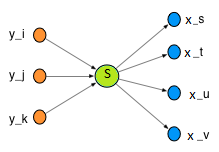
Сеть может быть построена из узлов, представляющих авторов, и ссылок, указывающих ссылки на опубликованные статьи. Исходящие ссылки показывают, кого цитировал автор, а входящие ссылки указывают, кто цитировал автора.
Оценка исследователя - это сумма оценок авторов, чьи работы цитируются. Оценка авторитета исследователя - это сумма оценок авторов, которые ссылались на работу исследователя.
Оценка хаба увеличивается, если автор цитирует статьи, опубликованные авторами с высокими авторитетными оценками. Рейтинг авторитета увеличивается, когда опубликованные статьи цитируются авторами с высоким рейтингом.
Уравнения можно переписать в матрично-векторном виде. Пусть A будет матрицей смежности сети, а векторы h и a содержат оценки всех узлов и органов власти соответственно. Затем баллы можно рассчитать по следующим формулам.[18]
Реализация хабов и алгоритма индекса авторитета
Индексы хабов и авторитетных источников требуют знания взаимосвязей между учеными, которые ссылаются на работы друг друга и цитируют их. Поскольку не всегда возможно точно получить эти шаблоны связности, можно оценить матрицу смежности (A), касающуюся связей ученого.
Например, у ученого есть оценочная матрица локальной связи. Это комбинация работ, на которые он ссылается, и работ, которые он цитирует. После оценки сети смежности индексы концентратора и авторитетности определяются собственное разложение из (A.A ’) и (A’.A) соответственно. Шаги, выполняемые для этой конкретной реализации, следующие:
- Шаг 1: Пусть оцениваемый ученый S. Этого ученого ищут в Scopus и общее количество полученных им цитирований = c, а общее количество использованных им ссылок =р.
- Шаг 2: Список ученых, которые цитировали работы S записываются как набор Y. Список ученых, привлеченных S записываются как Икс. Выбор членов Икс и Y делаются в порядке убывания цитирования в Scopus. Поскольку оценка матрицы смежности А было достаточно, поэтому мы записали участников Икс, и Y с цитированием более 100 в Scopus. Пусть количество значимых цитат = cs, а количество значимых ссылок = рs. Для каждого значимого члена Икс и Y, отношение (количество цитирований / количество ссылок) оценивается как веса матрицы А.
- Шаг 3: Как только веса, соответствующие значимым членам Икс и Y рассчитываются веса не столь значимых членов, оцениваются случайным образом. Таким образом, случайные веса генерируются для c − cs цитаты для членов Y и р − рs ссылки для членов Икс. Матрица А таким образом создается как:
| А | Столбец | S | Икс | Y |
|---|---|---|---|---|
| Индекс строки | S | 0 | 1 | 0 |
| Икс | 0 | 0 | 0 | |
| Y | 1 | 0 | 0 |
Где блоки X и блоки Y заменяют «1». Связь соответствует рисунку 2.

- Шаг 4. Начальный вектор концентратора вычисляется как первичный. собственный вектор (с наибольшим собственным значением) A.A ’ и нормализовано между [0,1]. Начальный авторитетный вектор - это первичный собственный вектор A’.A и нормализованный тоже. Поскольку эти индексы взаимосвязаны, вектор концентратора становится начальным вектором полномочий A *, а вектор полномочий становится вектором начального концентратора A ’*. Поскольку ученый «S» был первой записью в матрице A, следовательно, первое значение векторов хаба и авторитета являются индексами хаба-авторитета для ученого S. Псевдокод для них выглядит следующим образом: S ученый, чей индекс центра час и индекс авторитета а.
Псевдокод
1
2
3
4
Пример 1: научные индексы известных ученых
| Ученый | h-index (с использованием Publish или Perish) [2] | g-index (с помощью Publish или Perish)[2] | h-индекс (с использованием Scopus )[4] | Индекс хаба (на 10 ^ 2)[4] | Индекс авторитета [4] |
|---|---|---|---|---|---|
| Ньюман, MEJ | 65 | 210 | 51 | 210.54 | 129.3687 |
| Эйнштейн, Альберт | 92 | 231 | N / A (ничего не представлено после 1995 г.) | 0 | 99.9586 |
| Шеннон, CE | 44 | 228 | N / A (после 1995 года ничего не представлено) | 0 | 15.9117 |
| Эрдеш, Пол | 76 | 142 | 8 | 0.406490 | 77.8040 |
| Шенкер, Скотт | 105 | 253 | 36 | 29.173 | 171.1167 |
| Хирш, Хорхе Э. | 31 | 70 | 21 | 78.938 | 151.5361 |
| Попл, Джон | 87 | 293 | 29 | 123.7993 | 355.6553 |
В таблице используются Scopus только в качестве поисковой системы, а матрица смежности является оценкой, поэтому результаты, приведенные в таблице выше, представляют собой чрезвычайно агрегированные версии, и их не следует путать с абсолютными индексами. Более точная оценка матрицы смежности может привести к вариациям в индексах. Кроме того, Scopus отслеживает статьи только после 1995 г., так что это дополнительное ограничение. (Все индексы оценены по состоянию на 12 декабря 2011 г.)
Из этой таблицы видно, что разные поисковые системы дают разные h-индексы. Возможно, что ученый с высоким индексом Хирша может быть сильным авторитетом, но не обязательно сильным центром. Работоспособность поисковых систем оценивается как недоступность документов до 1995 года. Количество публикаций конкретного автора в конкретной базе данных влияет на индексы хаба. Междисциплинарная работа может быть хорошо оценена индексом авторитетности хаба в отличие от других индексов.
Пример 2: Прогнозируемые индексы авторитетности хаба со временем (игрушечный пример)
Это пример для понимания взаимодействия различных научных индексов.
Новый ученый, начавший свою академическую карьеру в 2009 году, опубликовал 3 статьи. Две статьи имеют по 2 ссылки каждая, а третья статья не цитируется. Она сослалась на 60 статей с 17 сильными ссылками из 60. У одного из ее соавторов самое низкое число Эрдеша 3. Ее научные индексы на декабрь 2011 года:
- индекс Хирша = 2
- g-индекс = 2
- m-частное = 2/2 = 1
- Число Эрдёша = 3 + 1 = 4
- Индекс HUB (на 10 ^ 2) = 11,702
- Индекс AUTHORITY = 0,1061
Через год она публикует еще одну статью с 20 новыми ссылками, так что теперь у нее в общей сложности 31 сильная ссылка, 4 статьи с 2 цитированием для 2 статей и 0 ссылок для других 2 статей. Индексы ее хаб-авторитета меняются:
Индекс HUB = 12,668
Индекс AUTHORITY = 0,1061
Через год ее количество цитирований 3 статей увеличилось до 10, и она продолжает иметь 60 ссылок с 17 сильными ссылками:
Индекс HUB = 11,568
Индекс AUTHORITY = 0,3241
Через год ее количество цитирований увеличивается до 10, и она пишет еще одну статью, в которой количество ссылок достигает 80 (с 31 сильной):
Индекс HUB = 12,694
Индекс AUTHORITY = 0,3284
Таким образом, для этого игрушечного примера наблюдаются следующие индексы хаба-авторитета.
| Пример | Количество цитат | Кол-во ссылок | HUB (на 10 ^ 2) | ОРГАН ВЛАСТИ |
|---|---|---|---|---|
| В настоящее время | 4 | 60 | 11.702 | 0.1061 |
| Если ссылки увеличиваются | 4 | 80 | 12.668 | 0.1061 |
| Если цитирования увеличиваются | 10 | 60 | 11.568 | 0.3241 |
| Если количество цитирований и ссылок увеличится | 10 | 80 | 12.694 | 0.3284 |
Код Matlab для примеров примеров 1 и Toy в Примере 2 прикреплен как Файл 1.

Эти примеры демонстрируют важность индексов хаб-авторитета в количественной оценке вклада ученого в полную академическую карьеру.
Критика
У научных указателей есть ограничения, в том числе отсутствие точности, достоверности и применимости. Хотя точность индексов ученых сомнительна из-за различий в написании, различий в синтаксическом анализаторе, поисковых системах и базах данных документов, поддерживаемых различными онлайн-источниками, можно было бы решить проблемы с точностью, если бы каждому автору был присвоен уникальный идентификатор. вместо того, чтобы полагаться на имена при поиске. Также каждый раз, когда публикуются эти индексы, необходимо упоминать используемые методы и поисковые системы, чтобы избежать двусмысленности, насколько это возможно.
Достоверность научных индексов является ограничением, поскольку они не взвешивают области различной важности. Например, Джон Попл химик-теоретик, получивший Нобелевскую премию, плохо справляется с наборами h-индексов.
Применимость научных индексов имеет ограничения, когда ученые делают упор на практическом продвижении в какой-либо области, а не на публикации статей. Также сложно задокументировать работы более раннего десятилетия в виде онлайн-документов, что снижает их онлайн-доступ. фактор воздействия. Например, Scopus это онлайн-база данных, которая рассчитывает индексы ученых для документов, найденных только после 1995 года. Более ранние работы не документируются и не оцениваются.
Хорхе Э. Хирш предложил индекс Хирша должны информировать комитеты по найму, продвижению по службе, финансированию, срокам полномочий, вознаграждениям и обществу для принятия разумных решений. Однако из-за их ограничений на них лучше всего смотреть сбалансированно.
Рекомендации
- ^ а б Макдональд, Ким (8 ноября 2005 г.). «Физик предлагает новый способ ранжирования научных результатов». PhysOrg. Получено 13 мая 2010.
- ^ а б c Perish Software Harzing, A.W. (2007) Publish or Perish, доступно по адресу http://www.harzing.com/pop.htm
- ^ http://www.cs.odu.edu/~mln/pubs/2007-10-09-h-index.html
- ^ а б c d https://www.scopus.com/home.url
- ^ https://scholar.google.com/
- ^ Мохаммад Хамдака и А. Хаму-Лхадж, «Анализ цитирования: подход к облегчению понимания и анализа нормативных документов», In Proc. 6-й Международной конференции по информационным технологиям, Лас-Вегас, США
- ^ Кир, Робин и Кольбер-Льюис, Даниэль (2011). «Цитирование и библиометрические измерения». Новости колледжей и исследовательских библиотек. 72 (8): 470–474. Дои:10.5860 / crln.72.8.8620.
- ^ Аманда Л. Верхейн, UW-Мэдисон. «Индекс Хирша научной продукции: новый показатель, продолжающиеся дискуссии» (PDF). Получено 22 апреля 2014.
- ^ Чжан, Си-Т (2009). «Электронный индекс, дополняющий h-индекс для избыточных цитирований». PLoS ONE. 4 (5): e5429. Дои:10.1371 / journal.pone.0005429. ЧВК 2673580. PMID 19415119.
- ^ Проект числа Эрдёша. http://www.oakland.edu/enp/
- ^ http://arnetminer.org/viewperson.do?aid=833230&name=C.%20E.%20Shannon (Х-индекс Шеннона)
- ^ https://scholar.google.it/citations?hl=it&user=2M6S-aAAAAAJ
- ^ ЛЕО ЯЙЦО (2006). «Теория и практика g-индекса». Наукометрия. 69 (1): 131–152. Дои:10.1007 / s11192-006-0144-7. HDL:1942/981.
- ^ Хабы и органы власти.http://nlp.stanford.edu/IR-book/html/htmledition/hubs-and-authorities-1.html
- ^ Хабы и органы власти.http://www.cs.ucr.edu/~vagelis/classes/CS172/publications/kleinberg98authoritative.pdf
- ^ Справочная терминология
- ^ Иерархический анализ ссылок для ранжирования веб-данных. http://renaud.delbru.fr/doc/pub/eswc2010-ding-slides.pdf
- ^ Алгоритм HITS - центры и органы в Интернете. http://www.math.cornell.edu/~mec/Winter2009/RalucaRemus/Lecture4/lecture4.html











