Тормозная способность (излучение частиц) - Stopping power (particle radiation)

В ядерной физике и физике материалов, останавливающая сила - тормозящая сила, действующая на заряженные частицы, обычно альфа и бета-частицы, из-за взаимодействия с веществом, что приводит к потере энергии частицы. [1][2]Его применение важно в таких областях, как радиационная защита, ионная имплантация и ядерная медицина.[3]

График, показывающий взаимосвязь между радиоактивностью и обнаруженным ионизирующим излучением

Определение и кривая Брэгга

И заряженные, и незаряженные частицы теряют энергию при прохождении через вещество. Положительные ионы рассматриваются в большинстве случаев ниже. Тормозная способность зависит от типа и энергии излучения, а также от свойств материала, через который оно проходит. Поскольку производство ион пара (обычно положительный ион и (отрицательный) электрон) требует фиксированного количества энергии (например, 33,97 эВ в сухом воздухе[4]:305) число ионизаций на длину пути пропорционально тормозной способности. В останавливающая сила материала численно равна потере энергии E на единицу длины пути, Икс:

Знак минус делает S положительным.

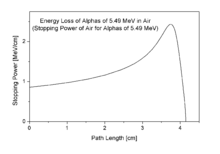
Кривая Брэгга 5,49 МэВ альфа-частицы в воздухе

Сила обычно увеличивается к концу классифицировать и достигает максимума, Пик Брэгга, незадолго до того, как энергия упадет до нуля. Кривая, описывающая силу как функцию глубины материала, называется Кривая Брэгга. Это имеет большое практическое значение для радиационная терапия.

Уравнение выше определяет линейная тормозная способность который в международной системе выражается в N но обычно указывается в других единицах, например MэВ / мм или аналогичный. Если сравнивать вещество в газообразной и твердой форме, то линейные тормозные способности этих двух состояний сильно различаются только из-за разной плотности. Поэтому часто делят силу на плотность материала для получения массовая останавливающая способность который в международной системе выражается в м4/s2 но обычно выражается в таких единицах, как МэВ / (мг / см2) или похожие. В этом случае тормозная способность массы очень мало зависит от плотности материала.

На картинке видно, как останавливающая сила 5,49 МэВ альфа-частицы увеличиваются, пока частица пересекает воздух, пока не достигнет максимума. Эта конкретная энергия соответствует энергии альфа-излучения естественных радиоактивный газ радон (222Rn), который присутствует в воздухе в ничтожных количествах.

Значение классифицировать можно рассчитать по интеграция взаимная тормозная сила над энергией:[5]

куда:

E0 - начальная кинетическая энергия частицы
Δx это диапазон «приближения непрерывного замедления (CSDA)» и
S (E) - линейная тормозная способность.

Выделяемая энергия может быть получена путем интегрирования тормозной способности по всей длине пути иона, когда он движется в материале.

Электронная, ядерная и радиационная остановка

Электронная остановка относится к замедлению иона-снаряда из-за неупругих столкновений между связанными электронами в среде и ионом, движущимся через нее. Термин неупругий используется для обозначения потери энергии в процессе (столкновения могут приводить как к возбуждению связанных электронов среды, так и к возбуждению электронного облака иона). Линейная электронная тормозная способность идентична неограниченная линейная передача энергии.

Вместо передачи энергии в некоторых моделях тормозная способность электронов рассматривается как передача импульса между электронным газом и энергичным ионом. Это согласуется с результатом Быть в диапазоне высоких энергий.[6]

Поскольку количество столкновений иона с электронами велико, и поскольку зарядовое состояние иона при прохождении через среду может часто меняться, очень трудно описать все возможные взаимодействия для всех возможных зарядовых состояний иона. Вместо этого электронную тормозную способность часто задают как простую функцию энергии. что является средним значением для всех процессов потери энергии для различных зарядовых состояний. Теоретически его можно определить с точностью до нескольких процентов в диапазоне энергий выше нескольких сотен кэВ на нуклон из теоретических подходов, наиболее известным из которых является Формула Бете. При энергиях ниже 100 кэВ на нуклон становится труднее определить электронное торможение с помощью аналитических моделей.[7] Недавно в реальном времени Теория функционала плотности, зависящая от времени успешно используется для точного определения электронного торможения для различных систем ион-мишень в широком диапазоне энергий, включая режим низких энергий.[8][9]

Электронная и ядерная тормозная способность для ионов алюминия в алюминии в зависимости от энергии частицы на нуклон. Максимум кривой ядерного торможения обычно наблюдается при энергиях порядка 1 кэВ на нуклон.

Графические представления экспериментальных значений электронной тормозной способности для многих ионов во многих веществах были даны Полом.[10] Точность различных таблиц остановки была определена с помощью статистических сравнений.[11]

Ядерная останавливающая сила относится к упругим столкновениям между ионом-снарядом и атомами в образце (установленное обозначение «ядерный» может сбивать с толку, поскольку ядерная остановка не происходит из-за ядерных сил,[12] но следует отметить, что этот тип остановки включает взаимодействие иона с ядра в мишени). Если знать вид потенциальной энергии отталкивания между двумя атомами (см. ниже), можно вычислить ядерную тормозную способность . На приведенном выше рисунке тормозной способности для ионов алюминия в алюминии ядерным торможением можно пренебречь, за исключением самой низкой энергии. Ядерная остановка увеличивается, когда масса иона увеличивается. На рисунке справа ядерная остановка больше, чем электронная остановка при низкой энергии. Для очень легких ионов, замедляющихся в тяжелых материалах, ядерное торможение слабее, чем электронное при всех энергиях.

Особенно в области радиационных повреждений в детекторах термин "неионизирующие потери энергии"(NIEL) используется как термин, противоположный линейная передача энергии (LET), см., Например, Ссылка[13][14][15] Поскольку по определению ядерная тормозная способность не связана с электронными возбуждениями, NIEL и ядерное торможение можно рассматривать как одну и ту же величину в отсутствие ядерных реакций.

Таким образом, полная нерелятивистская тормозная способность складывается из двух слагаемых: . Было разработано несколько полуэмпирических формул тормозной способности. Модель, предложенная Зиглером, Бирсаком и Литтмарком (так называемая остановка ZBL, см. Следующую главу),[16][17] реализован в разных версиях TRIM / SRIM коды,[18] сегодня используется чаще всего.

При чрезвычайно высоких энергиях ионов[3] необходимо также учитывать тормозную способность излучения, которая возникает из-за испускания тормозное излучение в электрических полях частиц в пройденном материале.[12] Для электронных снарядов всегда важна радиационная остановка. При высоких энергиях ионов также могут иметь место потери энергии из-за ядерных реакций, но такие процессы обычно не описываются тормозной способностью.[12]

Вблизи поверхности твердого материала мишени как ядерная, так и электронная остановка может привести к распыление.

Замедление процесса в твердых телах

Иллюстрация замедления одиночного иона в твердом материале

В начале процесса замедления при высоких энергиях ион замедляется в основном за счет электронной остановки, и он движется почти по прямой траектории. Когда ион достаточно замедлился, столкновения с ядрами (ядерное торможение) становятся все более и более вероятными, в конечном итоге доминируя над замедлением. Когда атомы твердого тела получают значительную энергию отдачи при ударе иона, они удаляются из своей решетка позиции, и произвести каскад дальнейших столкновений в материале. Эти каскады столкновений являются основной причиной образования повреждений при ионной имплантации в металлы и полупроводники.

Когда энергии всех атомов в системе упали ниже пороговая энергия смещения, производство новых повреждений прекращается, и концепция ядерной остановки теряет смысл. Общее количество энергии, передаваемой атомами в материалах в результате ядерных столкновений, называется ядерной вложенной энергией.

На вставке к рисунку показано типичное распределение ионов, осажденных в твердом теле. Показанный здесь случай может, например, быть замедлением иона кремния с энергией 1 МэВ в кремнии. Средний диапазон для иона 1 МэВ обычно находится в пределах микрометр классифицировать.

Отталкивающий межатомные потенциалы

На очень малых расстояниях между ядрами отталкивающее взаимодействие можно рассматривать как по существу кулоновское. На больших расстояниях электронные облака экранируют ядра друг от друга. Таким образом, потенциал отталкивания можно описать, умножив кулоновское отталкивание между ядрами на функцию экранирования φ (r / a),

где φ (r / a) → 1 при r → 0. Здесь и - заряды взаимодействующих ядер, а р расстояние между ними; а это так называемый параметр экранирования.

На протяжении многих лет было предложено большое количество различных потенциалов отталкивания и экранирующих функций, некоторые из которых определены полуэмпирически, другие - теоретическими расчетами. Часто используемый потенциал отталкивания - это так называемый потенциал отталкивания ZBL, предложенный Зиглером, Бирсаком и Литтмарком. Он был построен путем подгонки универсальной функции экранирования к теоретически полученным потенциалам, рассчитанным для большого разнообразия пар атомов.[16] Параметр и функция экранирования ZBL имеют вид

и

куда х = г / аты, и а0 - атомный радиус Бора = 0,529 Å.

Стандартное отклонение соответствия универсального потенциала отталкивания ZBL теоретически рассчитанным парным потенциалам, которым он соответствует, составляет 18% выше 2 эВ.[16] Еще более точные потенциалы отталкивания можно получить из самосогласованных расчетов полной энергии, используя теория функционала плотности и приближение локальной плотности (LDA) для электронного обмена и корреляции.[19]

Ченнелинг

Основная статья: Ченнелинг (физика)

В кристаллических материалах ион может в некоторых случаях получить "канал", т.е. сфокусироваться в канале между плоскостями кристалла, где он почти не сталкивается с ядрами. Кроме того, в канале может быть слабее электронное тормозное усилие. Таким образом, ядерное и электронное торможение зависит не только от типа и плотности материала, но также от его микроскопической структуры и поперечного сечения.

Компьютерное моделирование замедления ионов

Методы компьютерного моделирования для расчета движения ионов в среде разрабатывались с 1960-х годов и в настоящее время являются основным способом теоретического рассмотрения тормозной способности. Основная идея в них - проследить движение иона в среде путем моделирования столкновений с ядрами в среде. Электронная тормозная способность обычно учитывается как сила трения, замедляющая ион.

Обычные методы, используемые для расчета пробегов ионов, основаны на приближение бинарных столкновений (BCA).[20] В этих методах движение ионов в имплантированном образце рассматривается как последовательность отдельных столкновений между ионом отдачи и атомами в образце. Для каждого отдельного столкновения классический интеграл рассеяния решается путем численного интегрирования.

Прицельный параметр п в интеграле рассеяния определяется либо из стохастического распределения, либо таким образом, который учитывает кристаллическую структуру образца. Первый метод подходит только для моделирования имплантации в аморфные материалы, так как он не учитывает каналирование.

Самый известный BCA программа моделирования TRIM / SRIM (акроним для транспорта ионов в веществе, в более поздних версиях, называемых «Остановка и диапазон ионов в веществе»), который основан на электронной остановке ZBL и межатомный потенциал.[16][18][21] Он имеет очень простой в использовании пользовательский интерфейс и параметры по умолчанию для всех ионов во всех материалах с энергией до 1 ГэВ, что сделало его чрезвычайно популярным. Однако он не принимает во внимание кристаллическую структуру, что во многих случаях сильно ограничивает его полезность. Некоторые программы BCA преодолевают эту трудность; некоторые довольно известные - МАРЛОУ,[22] BCCRYS и crystal-TRIM.

Хотя методы BCA успешно использовались для описания многих физических процессов, они имеют некоторые препятствия для реалистичного описания процесса замедления энергичных ионов. Базовое предположение о том, что коллизии являются двоичными, приводит к серьезным проблемам при попытке учесть множественные взаимодействия. Кроме того, при моделировании кристаллических материалов процесс выбора следующего сталкивающегося атома решетки и прицельного параметра п всегда включают несколько параметров, которые могут иметь не совсем точно определенные значения, что может повлиять на результаты на 10–20% даже при вполне разумном выборе значений параметров. Наилучшая надежность в BCA достигается за счет включения нескольких коллизий в вычисления, что нелегко сделать правильно. Однако, по крайней мере, это делает МАРЛОУ.

Принципиально более простой способ моделирования множественных атомных столкновений обеспечивается молекулярная динамика (МД) моделирование, в котором эволюция системы атомов во времени рассчитывается путем численного решения уравнений движения. Были разработаны специальные методы МД, в которых количество взаимодействий и атомов, участвующих в моделировании МД, было уменьшено, чтобы сделать их достаточно эффективными для расчета пробегов ионов.[23][24] Моделирование МД автоматически описывает ядерную останавливающую способность. Электронную тормозную способность можно легко включить в молекулярно-динамическое моделирование либо как силу трения. [23][25][26][27][24][28][29][30] или более продвинутым способом, также следя за нагревом электронных систем и соединяя электронные и атомные степени свободы.[31][32][33]

Минимальная ионизирующая частица

При превышении максимального значения тормозная способность уменьшается примерно как 1 / v2 с увеличением скорости частицы v, но после минимума снова увеличивается.[34] Минимальная ионизирующая частица (или mip) - это частица, средняя скорость потери энергии через вещество которой близка к минимуму. Во многих практических случаях релятивистские частицы (например, космические лучи мюоны ) являются минимально ионизирующими частицами. Важным свойством минимально ионизирующих частиц является то, что они для всех приблизительно верно, что куда и - обычные кинематические величины, работающие в режиме реального времени. Более того, все МИПы имеют почти одинаковую потерю энергии в материале, которая составляет: [35].

Смотрите также

Рекомендации

  1. ^ Брэгг, В. Х. (1905). «Об α-частицах радия и их потере пробега при прохождении через различные атомы и молекулы». Фил. Mag. 10 (57): 318. Дои:10.1080/14786440509463378.
  2. ^ Бор, Н. (1913). «К теории уменьшения скорости движущихся наэлектризованных частиц при прохождении через материю». Фил. Mag. 25 (145): 10. Дои:10.1080/14786440108634305.
  3. ^ а б Отчет 73 ICRU: Остановка ионов тяжелее гелия, Журнал ICRU, 5 № 1 (2005), Oxford Univ. Нажмите ISBN  0-19-857012-0
  4. ^ Подгорсак Э.Б., ред. (2005). Физика радиационной онкологии: пособие для учителей и студентов (PDF). Вена: Международное агентство по атомной энергии. ISBN  978-92-0-107304-4. Получено 25 ноября 2012.
  5. ^ Международная комиссия по радиационным единицам и измерениям (1970). Линейная передача энергии (PDF). Вашингтон, округ Колумбия. ISBN  978-0913394090. Отчет ICRU 16. Получено 1 декабря 2012.
  6. ^ Ян, С .; Ди Ли, Ди Ли; Гэн Ван, Гэн Ван; Ли Линь, Ли Линь; Tasch, A.F .; Банерджи, С. (2002). «Квантовая механическая модель электронной тормозной способности для ионов в свободном электронном газе». Технология ионной имплантации. 2002. Материалы 14-й Международной конференции по. С. 556–559. Дои:10.1109 / IIT.2002.1258065. ISBN  0-7803-7155-0.
  7. ^ П. Зигмунд: Остановка тяжелых ионов. Тракты Спрингера в современной физике Vol. 204 (2004) ISBN  3-540-22273-1
  8. ^ Зеб, М. Ахсан; Kohanoff, J .; Sánchez-Portal, D .; Arnau, A .; Juaristi, J. I .; Артачо, Эмилио (31.05.2012). "Электронная тормозная способность в золоте: роль d Электроны и аномалия H / He ». Письма с физическими проверками. 108 (22): 225504. arXiv:1205.1728. Дои:10.1103 / PhysRevLett.108.225504. PMID  23003620.
  9. ^ Уллах, Рафи; Корсетти, Фабиано; Санчес-Портал, Даниэль; Артачо, Эмилио (2015-03-11). «Электронная тормозная способность в узкозонном полупроводнике из первых принципов». Физический обзор B. 91 (12): 125203. arXiv:1410.6642. Bibcode:2015PhRvB..91l5203U. Дои:10.1103 / PhysRevB.91.125203.
  10. ^ Тормозная способность легких ионов
  11. ^ Пол, H (2006). «Сравнение последних таблиц тормозной способности для легких и средних и тяжелых ионов с экспериментальными данными и приложениями к дозиметрии лучевой терапии». Ядерные инструменты и методы в физических исследованиях B. 247 (2): 166–172. Bibcode:2006НИМПБ.247..166П. Дои:10.1016 / j.nimb.2006.01.059.
  12. ^ а б c Международная комиссия по радиационным единицам и измерениям (октябрь 2011 г.). Зельцер, Стивен М. (ред.). «Фундаментальные величины и единицы ионизирующего излучения» (PDF). Журнал ICRU (Пересмотренная ред.). 11 (1): НП.2 – НП. Дои:10.1093 / jicru / ndr012. PMID  24174259. Отчет ICRU 85a. Получено 14 декабря 2012.
  13. ^ Хухтинен, Мика (2002). «Моделирование неионизирующих потерь энергии и образования дефектов в кремнии». Ядерные инструменты и методы в физических исследованиях B. 491 (1–2): 194–215. Bibcode:2002NIMPA.491..194H. Дои:10.1016 / s0168-9002 (02) 01227-5.
  14. ^ Барри, Алабама; Houdayer, AJ; Hinrichsen, PF; Летурно, WG; Винсент, Дж (1995). «Энергетическая зависимость констант времени жизни в GaAs-светодиодах для протонов 1-500 МэВ». IEEE Transactions по ядерной науке. 42 (6): 2104–2107. Bibcode:1995ITNS ... 42.2104B. Дои:10.1109/23.489259.
  15. ^ Линдстрем, Г. (2001). «Радиационно-жесткие кремниевые детекторы - разработки коллаборации RD48 (ROSE)». Ядерные инструменты и методы в физических исследованиях A. 466 (2): 308–326. Bibcode:2001НИМПА.466..308Л. Дои:10.1016 / S0168-9002 (01) 00560-5.
  16. ^ а б c d J. F. Ziegler, J. P. Biersack и U. Littmark. В остановке и пробеге ионов в веществе, том 1, Нью-Йорк, 1985. Пергамон. ISBN  0-08-022053-3
  17. ^ Дж. Ф. Циглер, Дж. П. Бирсак и М. Д. Циглер: SRIM - Остановка и пробег ионов в веществе, SRIM Co., 2008. ISBN  0-9654207-1-X
  18. ^ а б Веб-сайт SRIM
  19. ^ Нордлунд, К; Рунеберг, N; Сундхольм, Д. (1997). «Отталкивающие межатомные потенциалы, рассчитанные с использованием методов Хартри-Фока и теории функционала плотности». Ядерные инструменты и методы в физических исследованиях B. 132 (1): 45. Bibcode:1997НИМПБ.132 ... 45Н. Дои:10.1016 / S0168-583X (97) 00447-3.
  20. ^ Робинсон, Марк; Торренс, Ян (1974). «Компьютерное моделирование каскадов атомных смещений в твердых телах в приближении двойных столкновений». Физический обзор B. 9 (12): 5008. Bibcode:1974ПхРвБ ... 9.5008Р. Дои:10.1103 / PhysRevB.9.5008.
  21. ^ Бирсак, Дж; Хаггмарк, Л. (1980). «Компьютерная программа Монте-Карло для транспорта энергичных ионов в аморфных мишенях ☆». Ядерные инструменты и методы. 174 (1): 257. Bibcode:1980NucIM.174..257B. Дои:10.1016 / 0029-554X (80) 90440-1.
  22. ^ Робинсон, М. (1992). «Компьютерное моделирование каскадов столкновений высоких энергий1». Ядерные инструменты и методы в физических исследованиях B. 67 (1–4): 396–400. Bibcode:1992НИМПБ..67..396Р. Дои:10.1016 / 0168-583X (92) 95839-J.
  23. ^ а б Нордлунд, К. (1995). «Молекулярно-динамическое моделирование пробегов ионов в диапазоне энергий 1–100 кэВ». Вычислительное материаловедение. 3 (4): 448–456. Дои:10.1016 / 0927-0256 (94) 00085-Q.
  24. ^ а б Бирдмор, Кейт; Grønbech-Jensen, Нильс (1998). «Эффективная схема молекулярной динамики для расчета профилей примесей за счет ионной имплантации». Физический обзор E. 57 (6): 7278–7287. arXiv:физика / 9901054. Bibcode:1998PhRvE..57.7278B. CiteSeerX  10.1.1.285.6727. Дои:10.1103 / PhysRevE.57.7278.
  25. ^ Хоблер, Г. (2001). «О полезной области применения моделирования молекулярной динамики в приближении взаимодействия отдачи». Ядерные инструменты и методы в физических исследованиях B. 180 (1–4): 203. Bibcode:2001НИМПБ.180..203Х. Дои:10.1016 / s0168-583x (01) 00418-9.
  26. ^ Чатурла, М. (1996). «Ионно-лучевая обработка кремния при кэВ энергии: исследование молекулярной динамики». Физический обзор B. 54 (23): 16683–16695. Bibcode:1996PhRvB..5416683C. Дои:10.1103 / PhysRevB.54.16683. PMID  9985796.
  27. ^ Смит, Р. (1997). «Молекулярно-динамическое моделирование ионной бомбардировки Ni {100} с энергией 0,1 - 2 кэВ». Радиационные эффекты и дефекты в твердых телах. 141: 425. Дои:10.1080/10420159708211586.
  28. ^ Дювенбек, А. (2007). «Продвижение электронов и электронное трение в каскадах атомных столкновений». Новый журнал физики. 9 (2): 38. Bibcode:2007NJPh .... 9 ... 38D. Дои:10.1088/1367-2630/9/2/038.
  29. ^ Хоу, М. (2000). «Нанесение кластеров AuN на поверхности Au (111). I. Моделирование в атомном масштабе». Физический обзор B. 62 (4): 2825. Bibcode:2000ПхРвБ..62.2825Н. Дои:10.1103 / PhysRevB.62.2825.
  30. ^ Бьоркас, К. (2009). «Оценка связи между смешиванием ионного пучка, электрон-фононной связью и образованием повреждений в Fe». Ядерные инструменты и методы в физических исследованиях B. 267 (10): 1830. Bibcode:2009НИМПБ.267.1830Б. Дои:10.1016 / j.nimb.2009.03.080.
  31. ^ Проннеке, С. (1991). «Влияние потерь энергии электронов на динамику тепловых всплесков в Cu» (PDF). Журнал материаловедения. 6 (3): 483. Bibcode:1991JMatR ... 6..483P. Дои:10.1557 / jmr.1991.0483.
  32. ^ Даффи, Д. М. (2007). «Включая эффекты электронного торможения и электрон-ионных взаимодействий в моделировании радиационных повреждений». Журнал физики: конденсированное вещество. 17 (1): 016207. Bibcode:2007JPCM ... 19a6207D. Дои:10.1088/0953-8984/19/1/016207.
  33. ^ Тамм, А. (2016). «Электрон-фононное взаимодействие в рамках классической молекулярной динамики». Физический обзор B. 94 (1): 024305. Bibcode:2016PhRvB..94a4305L. Дои:10.1103 / PhysRevB.94.014305.
  34. ^ http://pdg.lbl.gov/2005/reviews/passagerpp.pdf
  35. ^ http://pdg.lbl.gov/2005/reviews/passagerpp.pdf

дальнейшее чтение

  • (Линдхард 1963) Дж. Линдхард, М. Шарфф и Х. Э. Шиотт. Концепции диапазонов и диапазоны тяжелых ионов. Мат. Fys. Medd. Дэн. Vid. Сельск., 33 (14): 1, 1963.
  • (Смит 1997) Р. Смит (редактор), Столкновения атомов и ионов в твердых телах и на поверхностях: теория, моделирование и приложения, Cambridge University Press, Кембридж, Великобритания, 1997.

внешняя ссылка