Триангуляция поверхности - Surface triangulation


Триангуляция из поверхность означает
- а сеть треугольников, покрывающих данную поверхность частично или полностью, или
- то процедура создания точек и треугольников такой сети треугольников.
Подходы
В этой статье описывается создание сети из треугольников. В литературе есть статьи, посвященные оптимизации данной сети.
Триангуляции поверхности важны для
- визуализация поверхности и
- применение методы конечных элементов.
Триангуляция параметрически Определенная поверхность достигается просто путем триангуляции области определения (см. второй рисунок, изображающий Седло Обезьяны ). Однако треугольники могут различаться по форме и протяженности в пространстве объектов, что создает потенциальный недостаток. Это можно минимизировать с помощью адаптивных методов, которые учитывают ширину шага при триангуляции области параметров.
Для триангуляции неявная поверхность (определяется одним или несколькими уравнениями) сложнее. По сути, существует два метода.
- Один метод разделяет рассматриваемую трехмерную область на кубы и определяет пересечения поверхности с краями кубов, чтобы получить на поверхности многоугольники, которые после этого необходимо триангулировать (метод резки куба).[1][2] Затраты на управление данными велики.
- Вторая и более простая концепция - это походный метод.[3][4][5] Триангуляция начинается с треугольного шестиугольника в начальной точке. Затем этот шестиугольник окружен новыми треугольниками, следуя заданным правилам, до тех пор, пока рассматриваемая поверхность не будет триангулирована. Если поверхность состоит из нескольких компонентов, алгоритм необходимо запускать несколько раз, используя подходящие начальные точки.
Алгоритм разрезания куба определяет одновременно все компоненты поверхности в окружающем начальном кубе в зависимости от заданных предельных параметров. Достоинством походного метода является возможность задания границ (см. Рисунок).
Полигонизация поверхность означает создание полигональная сетка.
Не следует путать триангуляцию поверхности с триангуляцией поверхности. дискретный предписанный самолет набор точек. Видеть Триангуляция Делоне.

Триангуляция: цилиндр, поверхность

Триангуляция: цилиндр, поверхность , Пов-луч изображение
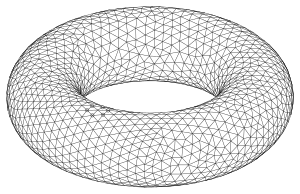
Тор: триангулированный маршевым методом

Тор: многоугольник методом разрезания куба
Смотрите также
- Системы автоматизированного проектирования
- Генерация сетки
- Тесселяция (компьютерная графика)
- Маршевые кубики
- Триангуляция набора точек
Рекомендации
- ^ М. Шмидт: Cutting Cubes - визуализация неявных поверхностей с помощью адаптивной полигонизации. Визуальный компьютер (1993) 10, стр. 101–115.
- ^ Дж. Блументаль: Полигонизация неявных поверхностей, Компьютерное геометрическое проектирование (1988), стр. 341–355.
- ^ Э. Хартманн: Геометрия и алгоритмы автоматизированного проектирования, п. 81 год
- ^ Э. Хартманн: Маршевый метод триангуляции поверхностей, Визуальный компьютер (1998), 14, стр. 95–108.
- ^ С. Аккуче и Э. Галин: Адаптивная неявная полигонизация поверхности с использованием марширующих треугольников, Форум КОМПЬЮТЕРНОЙ ГРАФИКИ (2001), Т. 20. С. 67–80.
внешняя ссылка
- Тассо Карканис и А. Джеймс Стюарт: Зависящая от кривизны триангуляция неявных поверхностей [1]





