Уникально раскрашиваемый график - Uniquely colorable graph
В теория графов, а однозначно раскрашиваемый граф это k-хроматический граф, который имеет только один возможный (собственно) k-крашивание вплоть до перестановка цветов. Эквивалентно, есть только один способ разбить его вершины на k независимые множества и нет возможности разделить их на k−1 независимых множеств.
Примеры
А полный график уникально раскрашивается, потому что единственная правильная раскраска - это та, которая присваивает каждой вершине другой цвет.
Каждые k-дерево однозначно (k + 1) -раскрашиваемый. Уникальный 4-цветный планарные графы как известно, именно Аполлонические сети, то есть плоские 3-деревья (Фаулер 1998 ).
Свойства
Некоторые свойства уникального kраскрашиваемый график г с участием п вершины и м края:
- м ≥ (k - 1) п - k(k-1)/2. (Трушчинский 1984; Сюй 1990 )
Связанные понятия
Минимальное несовершенство
А минимальный несовершенный граф является графом, в котором каждый подграф идеально. Удаление любой вершины из минимального несовершенного графа оставляет однозначно раскрашиваемый подграф.
Уникальная окраска кромок
А однозначно раскрашиваемый граф это kкромочно-хроматический граф, который имеет только один возможный (собственно) k-кратная окраска вплоть до перестановки цветов. Единственные графы, раскрашиваемые по двум ребрам, - это пути и циклы. Для любого k, то звезды K1,k единственные уникально k-кратно раскрашиваемые графы. Более того, Уилсон (1976) предположил и Томасон (1978) доказал, что когда k ≥ 4, они также единственные члены в этой семье. Однако существуют однозначно раскрашиваемые по 3 краям графы, которые не вписываются в эту классификацию, такие как граф треугольная пирамида.
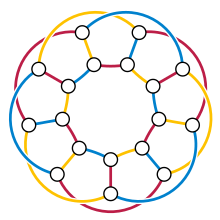
Если кубический граф однозначно раскрашивается 3 краями, у него должно быть ровно три Гамильтоновы циклы, образованный ребрами двух из трех его цветов, но некоторые кубические графы только с тремя гамильтоновыми циклами не являются однозначно 3-краскируемыми (Томасон 1982 ). Очень просто планарный кубический граф, однозначно раскрашиваемый по 3-ребрам, содержит треугольник (Фаулер 1998 ), но В. Т. Тутте (1976 ) заметил, что обобщенный граф Петерсена г(9,2) есть непланарный, без треугольников и с уникальной раскраской по 3 краям. В течение многих лет это был единственный известный такой граф, и предполагалось, что это единственный такой граф (см. Bollobás 1978 и Швенк 1989 ), но теперь известно бесконечно много непланарных кубических графов без треугольников, однозначно раскрашиваемых по 3-ребрам (belcastro & Haas 2015 ).
Уникальная общая окрашиваемость
А однозначно полный раскрашиваемый граф это k-общий-хроматический график у этого есть только один возможный (собственно) k-общая-окраска вплоть до перестановки цветов.
Пустые графики, пути, и циклы длины, кратной 3, являются однозначно полными раскрашиваемыми графами.Махмудиан и Шокроллахи (1995) предположил, что они также единственные члены в этой семье.
Некоторые свойства уникального k-общий раскрашиваемый график г с участием п вершины:
- χ ″ (г) = Δ (г) + 1, если г = K2. (Акбари и др. 1997 г. )
- Δ (г) ≤ 2 δ (г). (Акбари и др. 1997 г. )
- Δ (г) ≤ n / 2 + 1. (Акбари 2003 )
Здесь χ ″ (г) это общее хроматическое число; Δ (г) это максимальная степень; и δ (г) это минимальная степень.
использованная литература
- Акбари, С. (2003), "Две гипотезы об однозначно вполне раскрашиваемых графах", Дискретная математика, 266 (1–3): 41–45, Дои:10.1016 / S0012-365X (02) 00797-5, Г-Н 1991705.
- Акбари, С .; Бехзад, М .; Hajiabolhassan, H .; Махмудиан, Э. С. (1997), "Уникально полные раскрашиваемые графы", Графы и комбинаторика, 13 (4): 305–314, Дои:10.1016 / S0012-365X (02) 00797-5, Г-Н 1485924.
- белкастро, сара-мари; Хаас, Рут (2015), "Трехреберные однозначно раскрашиваемые кубические графы без треугольников", Вклад в дискретную математику, 10 (2): 39–44, arXiv:1508.06934, Bibcode:2015arXiv150806934B, Г-Н 3499076.
- Боллобаш, Бела (1978), Экстремальная теория графов, Монографии LMS, 11, Academic Press, Г-Н 0506522.
- Фаулер, Томас (1998), Уникальная раскраска плоских графов (PDF), Кандидат наук. диссертация, математический факультет Технологического института Джорджии.
- Хиллар, Кристофер Дж .; Windfeldt, Troels (2008), "Алгебраическая характеристика графов с уникальной раскраской вершин", Журнал комбинаторной теории, Серия B, 98 (2): 400–414, arXiv:математика / 0606565, Дои:10.1016 / j.jctb.2007.08.004, Г-Н 2389606.
- Махмудиан, Э. С .; Шокроллахи, М. А. (1995), "Открытые задачи на семинаре по комбинаторике AIMC25 (Тегеран, 1994)", в К. Дж., Колборн; Э. С., Махмудиан (ред.), Успехи комбинаторики, Математика и ее приложения, 329, Дордрехт; Бостон; Лондон: Kluwer Academic Publishers, стр. 321–324..
- Швенк, Аллен Дж. (1989), "Перечисление гамильтоновых циклов в некоторых обобщенных графах Петерсена", Журнал комбинаторной теории, Серия B, 47 (1): 53–59, Дои:10.1016/0095-8956(89)90064-6, Г-Н 1007713.
- Томасон, А. Г. (1978), "Гамильтоновы циклы и однозначно раскрашиваемые ребра графы", Достижения в теории графов (Кембриджская комбинаторная конференция, Тринити-колледж, Кембридж, 1977), Анналы дискретной математики, 3, стр. 259–268, Г-Н 0499124.
- Томасон, Эндрю (1982), "Кубические графы с тремя гамильтоновыми циклами не всегда однозначно раскрашиваются ребрами", Журнал теории графов, 6 (2): 219–221, Дои:10.1002 / jgt.3190060218, Г-Н 0655209.
- Трушчинский, М. (1984), «Некоторые результаты об однозначно раскрашиваемых графах», в Хайнал, А.; Ловас, Л.; Сош, В. Т. (ред.), Конечные и бесконечные множества. Vol. I, II. Труды шестого венгерского комбинаторного коллоквиума, проходившего в Эгере 6–11 июля 1981 г., Коллок. Математика. Soc. Янош Бойяи, 37, Северная Голландия, Амстердам, стр. 733–748, Г-Н 0818274.
- Тутте, Уильям Т. (1976), «Гамильтоновы схемы», Colloquio Internazionale sulle Teorie Combinatorie (Рим, 1973), Томо I, Accad. Наз. Линчеи, Рим, стр. 193–199. Atti dei Convegni Lincei, № 17, Г-Н 0480185. Как цитирует Белкастро и Хаас (2015).
- Сюй, Шао Цзи (1990), "Размер однозначно раскрашиваемых графов", Журнал комбинаторной теории, Серия B, 50 (2): 319–320, Дои:10.1016 / 0095-8956 (90) 90086-Ф, Г-Н 1081235.
- Уилсон, Р. Дж. (1976), «Проблема 2», в Нэш-Уильямс, К. Сент-Дж. А.; Шихан, Дж. (Ред.), Proc. Британский гребень. Конф. 1975 г., Виннипег: Utilitas Math., Стр. 696. Как цитирует Томасон (1978).
