Бинарное дерево без корня - Unrooted binary tree

А кладограмма в виде бинарного дерева без корней, представляющего сходство и историю эволюции между видами актинобактерии.

В математике и информатике некорневое двоичное дерево является неукорененное дерево в котором каждый вершина имеет одного или трех соседей.

Определения

А бесплатное дерево или неукорененное дерево - это связаны неориентированный граф без циклы. Вершины с одним соседом - это листья дерева, а оставшиеся вершины - внутренние узлы дерева. В степень вершины - количество ее соседей; в дереве с более чем одним узлом листья - это вершины первой степени. Бинарное дерево без корней - это свободное дерево, в котором все внутренние узлы имеют степень ровно три.

В некоторых приложениях может иметь смысл различать подтипы бинарных деревьев без корней: планарное вложение дерева можно зафиксировать, задав циклический порядок ребер в каждой вершине, превратив его в посадить дерево. В информатике бинарные деревья часто имеют корень и упорядочиваются, когда они используются как структуры данных, но в приложениях некорневых двоичных деревьев в иерархическая кластеризация и эволюционное дерево реконструкции, чаще встречаются неупорядоченные деревья.^[1]

Кроме того, можно различать деревья, в которых все вершины имеют разные метки, деревья, в которых помечены только листья, и деревья, в которых узлы не помечены. В некорневом двоичном дереве с п уходит, будет п - 2 внутренних узла, поэтому метки могут быть взяты из набора целых чисел от 1 до 2п - 1, если нужно пометить все узлы, или из набора целых чисел от 1 до п когда маркируются только листья.^[1]

Связанные структуры

Бинарные деревья с корнями

Бинарное дерево без корней Т может быть преобразован в полноценный двоичное дерево (то есть корневое дерево, в котором каждый нелистовой узел имеет ровно два дочерних элемента) путем выбора корневой край е из Т, помещая новый корневой узел в середину е, и направляя каждое ребро получившегося разбитого дерева от корневого узла. И наоборот, любое двоичное дерево с полным корнем может быть преобразовано в двоичное дерево без корня путем удаления корневого узла, замены пути между двумя его дочерними элементами одним неориентированным ребром и подавления ориентации остальных ребер в графе. По этой причине их ровно 2п −3 раза больше полных корневых двоичных деревьев с п листья, так как есть неуправляемые бинарные деревья с п листья.^[1]

Иерархическая кластеризация

А иерархическая кластеризация коллекции объектов можно формализовать как максимальный семейство наборов объектов, в которых не пересекаются никакие два набора. То есть на каждые два набора S и Т в семье либо S и Т не пересекаются, или один является подмножеством другого, и при сохранении этого свойства нельзя добавить больше наборов в семейство. Если Т является бинарным деревом без корня, оно определяет иерархическую кластеризацию своих листьев: для каждого ребра (ты,v) в Т есть гроздь, состоящая из листьев, находящихся ближе к ты чем v, и эти множества вместе с пустым множеством и множеством всех листьев образуют максимальное непересекающееся семейство. Наоборот, из любого максимального непересекающегося семейства множеств над множеством п элементов, можно сформировать уникальное некорневое двоичное дерево, имеющее узел для каждой тройки (А,B,C) непересекающихся множеств в семействе, которые вместе покрывают все элементы.^[2]

Эволюционные деревья

По простым формам теория эволюции, историю жизни можно резюмировать как филогенетическое дерево в котором каждый узел описывает вид, листья представляют виды, существующие сегодня, а края представляют отношения между предками и потомками между видами. Это дерево имеет естественную ориентацию от предков к потомкам, а корень находится в общий предок вида, так что это корневое дерево. Однако некоторые методы восстановления двоичных деревьев могут восстановить только узлы и ребра этого дерева, но не их ориентацию.

Например, кладистические методы Такие как максимальная экономия использовать в качестве данных набор двоичных атрибутов, описывающих особенности вида. Эти методы ищут дерево с заданными видами в виде листьев, в которых внутренние узлы также помечены характеристиками, и пытаются минимизировать количество раз, когда какой-либо элемент присутствует только в одной из двух конечных точек ребра в дереве. В идеале каждая функция должна иметь только одно ребро, для которого это так. Изменение корня дерева не меняет это количество различий между краями, поэтому методы, основанные на экономии, не могут определить местоположение корня дерева и будут производить дерево без корня, часто это двоичное дерево без корня.^[3]

Бинарные деревья без корней также создаются методами вывода эволюционных деревьев на основе данных квартета, определяющих для каждого четырехлистного вида неукорененное двоичное дерево, описывающее эволюцию этих четырех видов, и методами, которые используют квартетная дистанция для измерения расстояния между деревьями.^[4]

Ветка-разложение

Бинарные деревья без корня также используются для определения разложения по ветвям графов, формируя бинарное дерево без корней, листья которого представляют ребра данного графа. То есть разложение по ветвям можно рассматривать как иерархическую кластеризацию ребер графа. Разбиение ветвей и соответствующая числовая величина, ширина разветвления, тесно связаны с ширина дерева и формируют основу для эффективных динамическое программирование алгоритмы на графах.^[5]

Перечисление

Поскольку они используются в иерархической кластеризации, наиболее естественным перечисление графов проблема с некорневыми двоичными деревьями состоит в том, чтобы подсчитать количество деревьев с п маркированные листья и немаркированные внутренние узлы. Бинарное дерево без корней на п маркированные листья могут быть сформированы путем соединения п-й лист к новому узлу в середине любого из ребер неуправляемого двоичного дерева на п - 1 маркированный лист. Есть 2п - 5 ребер, на которых пый узел можно прикрепить; следовательно, количество деревьев на п листьев больше, чем количество деревьев на п - 1 лист в 2 разап - 5. Таким образом, количество деревьев на п маркированные листья - это двойной факториал

{ displaystyle (2n-5) !! = { frac {(2n-4)!} {(n-2)! 2 ^ {n-2}}}.}

^[6]

Количество деревьев на 2, 3, 4, 5, ... маркированных листьях равно

1, 1, 3, 15, 105, 945, 10395, 135135, 2027025, 34459425, ... (последовательность A001147 в OEIS ).

Фундаментальные равенства

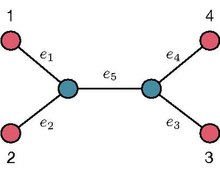
Длина пути от листа к листу на фиксированном некорневом двоичном дереве (UBT) T кодирует количество ребер, принадлежащих уникальному пути в T, соединяющему данный лист с другим листом. Например, обращаясь к UBT, показанному на изображении справа, длина пути ${ displaystyle p_ {1,2}}$ между листами 1 и 2 равно 2, тогда как длина пути ${ displaystyle p_ {1,3}}$ между листами 1 и 3 равно 3. Последовательность длины пути от данного листа на фиксированном UBT T кодирует длины путей от данного листа до всех остальных. Например, обращаясь к UBT, показанному на изображении справа, последовательность длины пути из листа 1 будет ${ displaystyle p_ {1} = (p_ {1,2}, p_ {1,3}, p_ {1,4}) = (2,3,3)}$ . Набор последовательностей длины пути, связанных с листами T, обычно называется коллекция последовательностей длины пути Т ^[7].

Пример бинарного дерева без корней с четырьмя листьями

Даниэле Катандзаро, Раффаэле Пезенти и Лоуренс Вулси показал^[8] что набор последовательностей длины пути, кодирующий данный UBT с n листами, должен удовлетворять определенным равенствам, а именно

${ displaystyle p_ {i, i} = 0}$ для всех ${ Displaystyle я в [1, п]}$
${ displaystyle p_ {i, j} = p_ {j, i}}$ для всех ${ displaystyle i, j in [1, n]: i neq j}$
${ displaystyle p_ {i, i} leq p_ {i, k} + p_ {k, j}}$ для всех ${ Displaystyle я, j, к в [1, n]: я neq j neq k}$
${ displaystyle sum _ {j = 1} ^ {n} 1/2 ^ {p_ {i, j}} = 1/2}$ для всех ${ Displaystyle я в [1, п]}$ (который является адаптацией Неравенство Крафт-Макмиллана )
${ displaystyle sum _ {я = 1} ^ {n} sum _ {j = 1} ^ {n} p_ {i, j} / 2 ^ {p_ {i, j}} = 2n-3}$ , также называемый филогенетическое многообразие^[9].

Доказано, что эти равенства необходимы и независимы для набора длины пути для кодирования UBT с n листами^[10]. В настоящее время неизвестно, достаточны ли они.

Альтернативные названия

Бинарные деревья без корня также называются бесплатные бинарные деревья,^[11] кубические деревья,^[12] тройные деревья^[5] и неукорененные тройные деревья,.^[13] Однако имя «свободное двоичное дерево» также применялось к некорневым деревьям, которые могут иметь узлы второй степени.^[14] и корневым двоичным деревьям с неупорядоченными дочерними элементами,^[15] а название "троичное дерево" чаще используется для обозначения корневое дерево с тремя дочерними элементами на узел.

Примечания

^ ^а ^б ^c Фурнаш (1984).
^ См. Например Эппштейн (2009) для того же соответствия между кластеризацией и деревьями, но с использованием корневых двоичных деревьев вместо некорневых деревьев и, следовательно, включая произвольный выбор корневого узла.
^ Хенди и Пенни (1989).
^ Сент-Джон и др. (2003).
^ ^а ^б Робертсон и Сеймур (1991).
^ Лысеющий, епископ и Каннингс (2007).
^ Катандзаро Д., Песенти Р., Вулси Л. (2020). «О сбалансированном многограннике минимальной эволюции». Дискретная оптимизация. 36: 100570. Дои:10.1016 / j.disopt.2020.100570.
^ Катандзаро Д., Песенти Р., Вулси Л. (2020). «О сбалансированном многограннике минимальной эволюции». Дискретная оптимизация. 36: 100570. Дои:10.1016 / j.disopt.2020.100570.
^ Катандзаро Д., Песенти Р., Вулси Л. (2020). «О сбалансированном многограннике минимальной эволюции». Дискретная оптимизация. 36: 100570. Дои:10.1016 / j.disopt.2020.100570.
^ Катандзаро Д., Песенти Р., Вулси Л. (2020). «О сбалансированном многограннике минимальной эволюции». Дискретная оптимизация. 36: 100570. Дои:10.1016 / j.disopt.2020.100570.
^ Чумадж и Гиббонс (1996).
^ Exoo (1996).
^ Чилибрази и Витаньи (2006).
^ Харари, Палмер и Робинсон (1992).
^ Пржитицка и Лармор (1994).