Кривая Циндлера - Википедия - Zindler curve

Рисунок 1: Кривая Циндлера. Любая из хорд одинаковой длины разрезает кривую и замкнутую область пополам.

Рисунок 2: Примеры кривых Циндлера с a = 8 (синий), a = 16 (зеленый) и a = 24 (красный).

А Кривая Циндлера это просто закрытый самолет изгиб с определяющим свойством

(L) Все аккорды, которые сокращают кривую длина пополам, иметь одинаковую длину.

Самыми простыми примерами кривой Циндлера являются круги. Австрийский математик Конрад Зиндлер обнаружил другие примеры и дал метод их построения. Герман Ауэрбах был первым, кто использовал (в 1938 г.) ныне устоявшееся название Кривая Циндлера.

Ауэрбах доказал, что фигура, ограниченная кривой Циндлера и имеющая половину плотности воды, будет плавать в воде в любом положении. Это дает отрицательный ответ на двумерную версию Станислав Улам о плавучих телах (Задача 19 Шотландская книга ), который спрашивает, является ли диск единственной фигурой с однородной плотностью, которая будет плавать в воде в любом положении (исходная задача спрашивает, является ли сфера единственным твердым телом, имеющим это свойство в трехмерном пространстве).

Кривые Циндлера также связаны с проблемой установления возможности определения направления движения велосипеда, учитывая только замкнутые задние и передние колеи.^[1]

Эквивалентные определения

Эквивалентное определение кривой Циндлера следующее:

(А) Все аккорды, которые сокращают площадь пополам, иметь одинаковую длину.

Эти хорды одинаковые, они разрезают кривую пополам.

Другое определение основано на каруселях Zindler с двумя стульями.^[2] Рассмотрим две гладкие кривые в р² определяется λ₁ и λ₂. Предположим, что расстояние между точками λ₁(t) и λ₂(t) постоянны для каждого т ∈ р и что кривая, определяемая серединами между λ₁ и λ₂ таков, что его касательный вектор в точке т параллельно отрезку из λ₁(т) к λ₂(т) для каждого т. Если кривые λ₁ и λ₂ параметризует ту же гладкую замкнутую кривую, тогда эта кривая будет кривой Циндлера.

Примеры

Рассмотрим фиксированный действительный параметр ${ displaystyle a}$. За ${ displaystyle a> 4}$, любая из кривых

${ displaystyle z (u) = x (u) + iy (u) = e ^ {2iu} + 2e ^ {- iu} + ae ^ {iu / 2} ;, u in [0,4 число Пи ];,}$

- кривая Циндлера.^[3] За ${ displaystyle a geq 24}$ кривая ровная выпуклый. На схеме показаны кривые для ${ displaystyle a = 8}$ (синий), ${ displaystyle a = 16}$ (зеленый) и ${ displaystyle a = 24}$ (красный). За ${ displaystyle a geq 8}$ кривые относятся к кривая постоянной ширины.

Рисунок 3: Пример кривой с a = 4 НЕ является кривой Циндлера, потому что есть желаемые хорды, которые пересекают кривую в третьей точке.

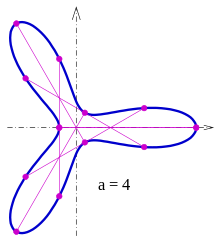
Доказательство чего-либо (L): Производная параметрического уравнения равна

${ displaystyle z '(u) = я { Big (} 2e ^ {2iu} -2e ^ {- iu} + { frac {a} {2}} e ^ {iu / 2} { Big)} ;}$ и

${ displaystyle | z '(u) | ^ {2} = z' (u) { overline {z '(u)}} = cdots = 8 + { frac {a ^ {2}} {4} } -8 cos 3u ;.}$

${ displaystyle | z '(u) |}$ является ${ displaystyle 2 pi}$-периодический Следовательно, для любого ${ displaystyle u_ {0}}$ имеет место следующее уравнение

${ displaystyle int _ {u_ {0}} ^ {u_ {0} +2 pi} | z '(u) | , du = int _ {0} ^ {2 pi} | z' ( u) | , du ;,}$

что составляет половину длины всей кривой. Искомые хорды, разделяющие кривую пополам, ограничены точками ${ Displaystyle ; z (u_ {0}) ;, ; z (u_ {0} +2 pi) ;}$ для любого ${ displaystyle u_ {0} in [0,4 pi]}$. Длина такого хорды составляет ${ displaystyle | z (u_ {0} +2 pi) -z (u_ {0}) | = cdots = | 2ae ^ {iu_ {0} / 2} | = 2a ;,}$ следовательно, независимо от ${ displaystyle u_ {0}}$. ∎

За ${ displaystyle a = 4}$ желаемые хорды пересекаются с кривой в дополнительной точке (см. рисунок 3). Следовательно, только для ${ displaystyle a> 4}$ примерные кривые - кривые Циндлера.

Обобщения

Свойство, определяющее кривые Циндлера, также может быть обобщено на хорды, которые пересекают периметр кривой в фиксированном отношении α, отличном от 1/2. В этом случае вместо всех хорд кривой можно рассматривать хордовую систему (непрерывный выбор хорд). Эти кривые известны как кривые α-Циндлера,^[4] и - кривые Циндлера при α = 1/2. Это обобщение кривой Зиндлера имеет следующее свойство, связанное с проблемой плавания: пусть γ - замкнутая гладкая кривая с системой хорд, пересекающей периметр в фиксированном соотношении α. Если все хорды этой хордовой системы находятся внутри области, ограниченной γ, то γ является α-кривой Циндлера тогда и только тогда, когда область, ограниченная γ, является телом равномерной плотности ρ, плавающим в любой ориентации.^[4]

Примечания

Рекомендации

• Герман Ауэрбах: Sur un problème de M. Ulam концерн l’équilibre des corps flottants (PDF; 796 kB), Studia Mathematica 7, 1938, стр. 121–142.
• К. Л. Мампель: Убер Зиндлеркурвен, Journal für reine und angewandte Mathematik 234, 1969, стр. 12–44.
• Конрад Зиндлер: Über konvexe Gebilde. II. Teil, Monatshefte für Mathematik und Physik 31, 1921, стр. 25–56.
• Х. Мартини, С. Ву: О кривых Циндлера в нормированных плоскостях, Канад. Математика. Бык. 55 (2012), 767–773.
• Х. Брачо, Л. Монтехано, Д. Оливерос:Карусели, кривые Зиндлера и проблема плавающего тела, Период Математики Хунг (2004) 49.
• П. М. Грубер, Дж. М. Уиллс: Выпуклость и ее приложения, Спрингер, 1983, ISBN  978-3-0348-5860-1, п. 58.

внешняя ссылка

• http://www.thphys.uni-heidelberg.de/~wegner/Fl2mvs/Movies.html - Страница Франца Вегнера с изображением некоторых тел, плавающих в любом направлении.
• https://www.rose-hulman.edu/~finn/research/bicycle/tracks.html - Страница Дэвида Л. Финна, иллюстрирующая пару кривых, по которым невозможно определить, какая из них является задней или передней колеей велосипеда.